Splitter (geometry)

The Nagel point (blue, N) of a triangle (black). The red triangle is the extouch triangle, and the orange circles are the excircles. The splitters of the perimeter are AT_A, BT_B, and CT_C.

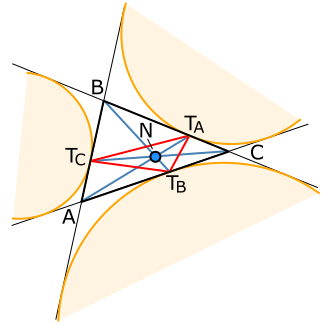
In plane geometry, a splitter is a line segment through one of the vertices of a triangle (that is, a cevian) that bisects the perimeter of the triangle.^[1][2]

Properties

The opposite endpoint of a splitter to the chosen triangle vertex lies at the point on the triangle's side where one of the excircles of the triangle is tangent to that side.^[1][2] This point is also called a splitting point of the triangle.^[2] It is additionally a vertex of the extouch triangle and one of the points where the Mandart inellipse is tangent to the triangle side.^[3]

The three splitters concur at the Nagel point of the triangle,^[1] which is also called its splitting center.^[2]

Generalization

Some authors have used the term "splitter" in a more general sense, for any line segment that bisects the perimeter of the triangle. Other line segments of this type include the cleavers, which are perimeter-bisecting segments that pass through the midpoint of a triangle side, and the equalizers, segments that bisect both the area and perimeter of a triangle.^[4]

References

External links

• Weisstein, Eric W.. "Splitter". http://mathworld.wolfram.com/Splitter.html. 

0.00 (0 votes)