Squeeze theorem
 From HandWiki - Reading time: 6 min
From HandWiki - Reading time: 6 min
In calculus, the squeeze theorem (also known as the sandwich theorem, among other names[lower-alpha 1]) is a theorem regarding the limit of a function that is trapped between two other functions.
The squeeze theorem is used in calculus and mathematical analysis, typically to confirm the limit of a function via comparison with two other functions whose limits are known. It was first used geometrically by the mathematicians Archimedes and Eudoxus in an effort to compute π, and was formulated in modern terms by Carl Friedrich Gauss.
Statement
The squeeze theorem is formally stated as follows.[1]
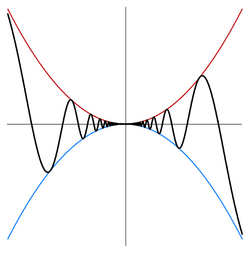
Theorem — Let I be an interval containing the point a. Let g, f, and h be functions defined on I, except possibly at a itself. Suppose that for every x in I not equal to a, we have [math]\displaystyle{ g(x) \leq f(x) \leq h(x) }[/math] and also suppose that [math]\displaystyle{ \lim_{x \to a} g(x) = \lim_{x \to a} h(x) = L. }[/math] Then [math]\displaystyle{ \lim_{x \to a} f(x) = L. }[/math]
- The functions g and h are said to be lower and upper bounds (respectively) of f.
- Here, a is not required to lie in the interior of I. Indeed, if a is an endpoint of I, then the above limits are left- or right-hand limits.
- A similar statement holds for infinite intervals: for example, if I = (0, ∞), then the conclusion holds, taking the limits as x → ∞.
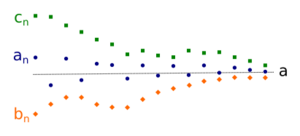
This theorem is also valid for sequences. Let (an), (cn) be two sequences converging to ℓ, and (bn) a sequence. If [math]\displaystyle{ \forall n\geq N, N\in\N }[/math] we have an ≤ bn ≤ cn, then (bn) also converges to ℓ.
Proof
According to the above hypotheses we have, taking the limit inferior and superior: [math]\displaystyle{ L=\lim_{x \to a} g(x)\leq\liminf_{x\to a}f(x) \leq \limsup_{x\to a}f(x)\leq \lim_{x \to a}h(x)=L, }[/math] so all the inequalities are indeed equalities, and the thesis immediately follows.
A direct proof, using the (ε, δ)-definition of limit, would be to prove that for all real ε > 0 there exists a real δ > 0 such that for all x with [math]\displaystyle{ |x - a| \lt \delta, }[/math] we have [math]\displaystyle{ |f(x) - L| \lt \varepsilon. }[/math] Symbolically,
[math]\displaystyle{ \forall \varepsilon \gt 0, \exists \delta \gt 0 : \forall x, (|x - a | \lt \delta \ \Rightarrow |f(x) - L |\lt \varepsilon). }[/math]
As
[math]\displaystyle{ \lim_{x \to a} g(x) = L }[/math]
means that
[math]\displaystyle{ \forall \varepsilon \gt 0, \exists \ \delta_1 \gt 0 : \forall x\ (|x - a| \lt \delta_1 \ \Rightarrow \ |g(x) - L |\lt \varepsilon). }[/math] |
|
() |
and [math]\displaystyle{ \lim_{x \to a} h(x) = L }[/math]
means that
[math]\displaystyle{ \forall \varepsilon \gt 0, \exists \ \delta_2 \gt 0 : \forall x\ (|x - a | \lt \delta_2\ \Rightarrow \ |h(x) - L |\lt \varepsilon), }[/math] |
|
() |
then we have
[math]\displaystyle{ g(x) \leq f(x) \leq h(x) }[/math] [math]\displaystyle{ g(x) - L\leq f(x) - L\leq h(x) - L }[/math]
We can choose [math]\displaystyle{ \delta:=\min\left\{\delta_1,\delta_2\right\} }[/math]. Then, if [math]\displaystyle{ |x - a| \lt \delta }[/math], combining (1) and (2), we have
[math]\displaystyle{ - \varepsilon \lt g(x) - L\leq f(x) - L\leq h(x) - L\ \lt \varepsilon, }[/math] [math]\displaystyle{ - \varepsilon \lt f(x) - L \lt \varepsilon , }[/math]
which completes the proof. Q.E.D
The proof for sequences is very similar, using the [math]\displaystyle{ \varepsilon }[/math]-definition of the limit of a sequence.
Examples
First example
The limit
[math]\displaystyle{ \lim_{x \to 0}x^2 \sin\left( \tfrac{1}{x} \right) }[/math]
cannot be determined through the limit law
[math]\displaystyle{ \lim_{x \to a}(f(x) \cdot g(x)) = \lim_{x \to a}f(x) \cdot \lim_{x \to a}g(x), }[/math]
because
[math]\displaystyle{ \lim_{x\to 0}\sin\left( \tfrac{1}{x} \right) }[/math]
does not exist.
However, by the definition of the sine function,
[math]\displaystyle{ -1 \le \sin\left( \tfrac{1}{x} \right) \le 1. }[/math]
It follows that
[math]\displaystyle{ -x^2 \le x^2 \sin\left( \tfrac{1}{x} \right) \le x^2 }[/math]
Since [math]\displaystyle{ \lim_{x\to 0}-x^2 = \lim_{x\to 0}x^2 = 0 }[/math], by the squeeze theorem, [math]\displaystyle{ \lim_{x\to 0} x^2 \sin\left(\tfrac{1}{x}\right) }[/math] must also be 0.
Second example
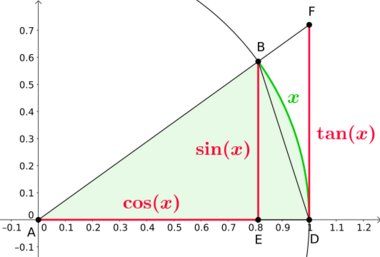
[math]\displaystyle{ \begin{array}{cccccc} & A(\triangle ADB) & \leq & A(\text{sector } ADB) & \leq & A(\triangle ADF) \\[4pt] \Rightarrow & \frac{1}{2} \cdot \sin x \cdot 1 & \leq & \frac{x}{2\pi} \cdot \pi & \leq & \frac{1}{2} \cdot \tan x \cdot 1 \\[4pt] \Rightarrow & \sin x & \leq & x & \leq & \frac{\sin x}{\cos x} \\[4pt] \Rightarrow & \frac{\cos x}{\sin x} & \leq & \frac{1}{x} & \leq & \frac{1}{\sin x} \\[4pt] \Rightarrow & \cos x & \leq & \frac{\sin x}{x} & \leq & 1 \end{array} }[/math]
Probably the best-known examples of finding a limit by squeezing are the proofs of the equalities [math]\displaystyle{ \begin{align} & \lim_{x\to 0} \frac{\sin x}{x} =1, \\[10pt] & \lim_{x\to 0} \frac{1 - \cos x}{x} = 0. \end{align} }[/math]
The first limit follows by means of the squeeze theorem from the fact that[2]
[math]\displaystyle{ \cos x \leq \frac{\sin x}{x} \leq 1 }[/math]
for x close enough to 0. The correctness of which for positive x can be seen by simple geometric reasoning (see drawing) that can be extended to negative x as well. The second limit follows from the squeeze theorem and the fact that
[math]\displaystyle{ 0 \leq \frac{1 - \cos x}{x} \leq x }[/math] for x close enough to 0. This can be derived by replacing sin x in the earlier fact by [math]\displaystyle{ \sqrt{1-\cos^2 x} }[/math] and squaring the resulting inequality.
These two limits are used in proofs of the fact that the derivative of the sine function is the cosine function. That fact is relied on in other proofs of derivatives of trigonometric functions.
Third example
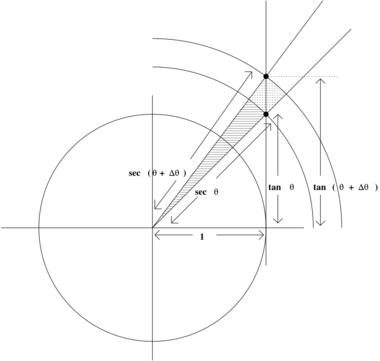
It is possible to show that [math]\displaystyle{ \frac{d}{d\theta} \tan\theta = \sec^2\theta }[/math] by squeezing, as follows.
In the illustration at right, the area of the smaller of the two shaded sectors of the circle is
[math]\displaystyle{ \frac{\sec^2\theta\,\Delta\theta}{2}, }[/math]
since the radius is sec θ and the arc on the unit circle has length Δθ. Similarly, the area of the larger of the two shaded sectors is
[math]\displaystyle{ \frac{\sec^2(\theta + \Delta\theta)\,\Delta\theta}{2}. }[/math]
What is squeezed between them is the triangle whose base is the vertical segment whose endpoints are the two dots. The length of the base of the triangle is tan(θ + Δθ) − tan θ, and the height is 1. The area of the triangle is therefore
[math]\displaystyle{ \frac{\tan(\theta + \Delta\theta) - \tan\theta}{2}. }[/math]
From the inequalities
[math]\displaystyle{ \frac{\sec^2\theta\,\Delta\theta}{2} \le \frac{\tan(\theta + \Delta\theta) - \tan\theta}{2} \le \frac{\sec^2(\theta + \Delta\theta)\,\Delta\theta}{2} }[/math]
we deduce that
[math]\displaystyle{ \sec^2\theta \le \frac{\tan(\theta + \Delta\theta) - \tan\theta}{\Delta\theta} \le \sec^2(\theta + \Delta\theta), }[/math]
provided Δθ > 0, and the inequalities are reversed if Δθ < 0. Since the first and third expressions approach sec2θ as Δθ → 0, and the middle expression approaches [math]\displaystyle{ \tfrac{d}{d\theta} \tan\theta, }[/math] the desired result follows.
Fourth example
The squeeze theorem can still be used in multivariable calculus but the lower (and upper functions) must be below (and above) the target function not just along a path but around the entire neighborhood of the point of interest and it only works if the function really does have a limit there. It can, therefore, be used to prove that a function has a limit at a point, but it can never be used to prove that a function does not have a limit at a point.[3]
[math]\displaystyle{ \lim_{(x,y) \to (0, 0)} \frac{x^2 y}{x^2+y^2} }[/math]
cannot be found by taking any number of limits along paths that pass through the point, but since
[math]\displaystyle{ \begin{array}{rccccc} & 0 & \leq & \displaystyle \frac{x^2}{x^2+y^2} & \leq & 1 \\[4pt] -|y| \leq y \leq |y| \implies & -|y| & \leq & \displaystyle \frac{x^2 y}{x^2+y^2} & \leq & |y| \\[4pt] { {\displaystyle \lim_{(x,y) \to (0, 0)} -|y| = 0} \atop {\displaystyle \lim_{(x,y) \to (0, 0)} \ \ \ |y| = 0} } \implies & 0 & \leq & \displaystyle \lim_{(x,y) \to (0, 0)} \frac{x^2 y}{x^2+y^2} & \leq & 0 \end{array} }[/math]
therefore, by the squeeze theorem,
[math]\displaystyle{ \lim_{(x,y) \to (0, 0)} \frac{x^2 y}{x^2+y^2} = 0. }[/math]
References
Notes
- ↑ Also known as the pinching theorem, the sandwich rule, the police theorem, the between theorem and sometimes the squeeze lemma. In Italy, the theorem is also known as the theorem of carabinieri.
References
- ↑ Sohrab, Houshang H. (2003). Basic Real Analysis (2nd ed.). Birkhäuser. p. 104. ISBN 978-1-4939-1840-9. https://books.google.com/books?id=QnpqBQAAQBAJ&pg=PA104.
- ↑ Selim G. Krejn, V.N. Uschakowa: Vorstufe zur höheren Mathematik. Springer, 2013, ISBN:9783322986283, pp. 80-81 (German). See also Sal Khan: Proof: limit of (sin x)/x at x=0 (video, Khan Academy)
- ↑ Stewart, James (2008). "Chapter 15.2 Limits and Continuity". Multivariable Calculus (6th ed.). pp. 909–910. ISBN 978-0495011637.
External links
- Weisstein, Eric W.. "Squeezing Theorem". http://mathworld.wolfram.com/SqueezingTheorem.html.
- Squeeze Theorem by Bruce Atwood (Beloit College) after work by, Selwyn Hollis (Armstrong Atlantic State University), the Wolfram Demonstrations Project.
- Squeeze Theorem on ProofWiki.
 |
 KSF
KSF