Stationary process
 From HandWiki - Reading time: 16 min
From HandWiki - Reading time: 16 min
In mathematics and statistics, a stationary process (also called a strict/strictly stationary process or strong/strongly stationary process) is a stochastic process whose statistical properties, such as mean and variance, do not change over time. More formally, the joint probability distribution of the process remains the same when shifted in time. This implies that the process is statistically consistent across different time periods. Because many statistical procedures in time series analysis assume stationarity, non-stationary data are frequently transformed to achieve stationarity before analysis.
A common cause of non-stationarity is a trend in the mean, which can be due to either a unit root or a deterministic trend. In the case of a unit root, stochastic shocks have permanent effects, and the process is not mean-reverting. With a deterministic trend, the process is called trend-stationary, and shocks have only transitory effects, with the variable tending towards a deterministically evolving mean. A trend-stationary process is not strictly stationary but can be made stationary by removing the trend. Similarly, processes with unit roots can be made stationary through differencing.
Another type of non-stationary process, distinct from those with trends, is a cyclostationary process, which exhibits cyclical variations over time.
Strict stationarity, as defined above, can be too restrictive for many applications. Therefore, other forms of stationarity, such as wide-sense stationarity or N-th-order stationarity, are often used. The definitions for different kinds of stationarity are not consistent among different authors (see Other terminology).
Strict-sense stationarity
Definition
Formally, let be a stochastic process and let represent the cumulative distribution function of the unconditional (i.e., with no reference to any particular starting value) joint distribution of at times . Then, is said to be strictly stationary, strongly stationary or strict-sense stationary if[1]: p. 155
|
|
() |
Since does not affect , is independent of time.
Examples
White noise is the simplest example of a stationary process.
An example of a discrete-time stationary process where the sample space is also discrete (so that the random variable may take one of N possible values) is a Bernoulli scheme. Other examples of a discrete-time stationary process with continuous sample space include some autoregressive and moving average processes which are both subsets of the autoregressive moving average model. Models with a non-trivial autoregressive component may be either stationary or non-stationary, depending on the parameter values, and important non-stationary special cases are where unit roots exist in the model.
Example 1
Let be any scalar random variable, and define a time-series by
Then is a stationary time series, for which realisations consist of a series of constant values, with a different constant value for each realisation. A law of large numbers does not apply on this case, as the limiting value of an average from a single realisation takes the random value determined by , rather than taking the expected value of .
The time average of does not converge since the process is not ergodic.
Example 2
As a further example of a stationary process for which any single realisation has an apparently noise-free structure, let have a uniform distribution on and define the time series by
Then is strictly stationary since ( modulo ) follows the same uniform distribution as for any .
Example 3
Keep in mind that a weakly white noise is not necessarily strictly stationary. Let be a random variable uniformly distributed in the interval and define the time series
Then
So is a white noise in the weak sense (the mean and cross-covariances are zero, and the variances are all the same), however it is not strictly stationary.
Nth-order stationarity
In Eq.1, the distribution of samples of the stochastic process must be equal to the distribution of the samples shifted in time for all . N-th-order stationarity is a weaker form of stationarity where this is only requested for all up to a certain order . A random process is said to be N-th-order stationary if:[1]: p. 152
|
|
() |
Weak or wide-sense stationarity
Definition
A weaker form of stationarity commonly employed in signal processing is known as weak-sense stationarity, wide-sense stationarity (WSS), or covariance stationarity. WSS random processes only require that 1st moment (i.e. the mean) and autocovariance do not vary with respect to time and that the 2nd moment is finite for all times. Any strictly stationary process which has a finite mean and covariance is also WSS.[2]: p. 299
So, a continuous time random process which is WSS has the following restrictions on its mean function and autocovariance function :
|
|
() |
The first property implies that the mean function must be constant. The second property implies that the autocovariance function depends only on the difference between and and only needs to be indexed by one variable rather than two variables.[1]: p. 159 Thus, instead of writing,
the notation is often abbreviated by the substitution :
This also implies that the autocorrelation depends only on , that is
The third property says that the second moments must be finite for any time .
Motivation
The main advantage of wide-sense stationarity is that it places the time-series in the context of Hilbert spaces. Let H be the Hilbert space generated by {x(t)} (that is, the closure of the set of all linear combinations of these random variables in the Hilbert space of all square-integrable random variables on the given probability space). By the positive definiteness of the autocovariance function, it follows from Bochner's theorem that there exists a positive measure on the real line such that H is isomorphic to the Hilbert subspace of L2(μ) generated by {e−2πiξ⋅t}. This then gives the following Fourier-type decomposition for a continuous time stationary stochastic process: there exists a stochastic process with orthogonal increments such that, for all
where the integral on the right-hand side is interpreted in a suitable (Riemann) sense. The same result holds for a discrete-time stationary process, with the spectral measure now defined on the unit circle.
When processing WSS random signals with linear, time-invariant (LTI) filters, it is helpful to think of the correlation function as a linear operator. Since it is a circulant operator (depends only on the difference between the two arguments), its eigenfunctions are the Fourier complex exponentials. Additionally, since the eigenfunctions of LTI operators are also complex exponentials, LTI processing of WSS random signals is highly tractable—all computations can be performed in the frequency domain. Thus, the WSS assumption is widely employed in signal processing algorithms.
Definition for complex stochastic process
In the case where is a complex stochastic process the autocovariance function is defined as and, in addition to the requirements in Eq.3, it is required that the pseudo-autocovariance function depends only on the time lag. In formulas, is WSS, if
|
|
() |
Joint stationarity
The concept of stationarity may be extended to two stochastic processes.
Joint strict-sense stationarity
Two stochastic processes and are called jointly strict-sense stationary if their joint cumulative distribution remains unchanged under time shifts, i.e. if
|
|
() |
Joint (M + N)th-order stationarity
Two random processes and is said to be jointly (M + N)-th-order stationary if:[1]: p. 159
|
|
() |
Joint weak or wide-sense stationarity
Two stochastic processes and are called jointly wide-sense stationary if they are both wide-sense stationary and their cross-covariance function depends only on the time difference . This may be summarized as follows:
|
|
() |
Relation between types of stationarity
- If a stochastic process is N-th-order stationary, then it is also M-th-order stationary for all .
- If a stochastic process is second order stationary () and has finite second moments, then it is also wide-sense stationary.[1]: p. 159
- If a stochastic process is wide-sense stationary, it is not necessarily second-order stationary.[1]: p. 159
- If a stochastic process is strict-sense stationary and has finite second moments, it is wide-sense stationary.[2]: p. 299
- If two stochastic processes are jointly (M + N)-th-order stationary, this does not guarantee that the individual processes are M-th- respectively N-th-order stationary.[1]: p. 159
Other terminology
The terminology used for types of stationarity other than strict stationarity can be rather mixed. Some examples follow.
- Priestley uses stationary up to order m if conditions similar to those given here for wide sense stationarity apply relating to moments up to order m.[3][4] Thus wide sense stationarity would be equivalent to "stationary to order 2", which is different from the definition of second-order stationarity given here.
- Honarkhah and Caers also use the assumption of stationarity in the context of multiple-point geostatistics, where higher n-point statistics are assumed to be stationary in the spatial domain.[5]
Techniques to stationarize a non-stationary process
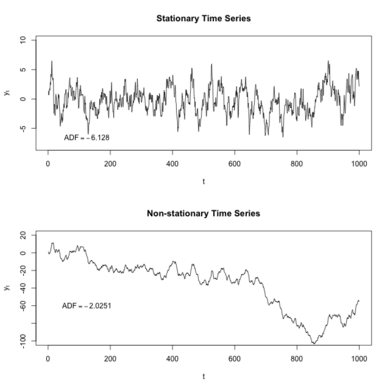
In time series analysis and stochastic processes, stationarizing a time series is a crucial preprocessing step aimed at transforming a non-stationary process into a stationary one. Several techniques exist for achieving this, depending on the type and order of non-stationarity present. For first-order non-stationarity, where the mean of the process varies over time, differencing is a common and effective method: it transforms the series by subtracting each value from its predecessor, thus stabilizing the mean. For non-stationarities up to the second order, time-frequency analysis (e.g., Wavelet transform, Wigner distribution function, or Short-time Fourier transform) can be employed to isolate and suppress time-localized, nonstationary spectral components. Additionally, surrogate data methods can be used to construct strictly stationary versions of the original time series. One of the ways for identifying non-stationary times series is the ACF plot. Sometimes, patterns will be more visible in the ACF plot than in the original time series; however, this is not always the case.[6]
The choice of method for time series stationarization depends on the nature of the non-stationarity and the goals of the analysis, especially when building models that require strict stationarity assumptions, such as ARMA or spectral-based techniques. More details on some time series stationarization methods are presented below.
Stationarization by means of differencing
One way to make some time series first-order stationary is to compute the differences between consecutive observations. This is known as differencing. Differencing can help stabilize the mean of a time series by removing changes in the level of a time series, and so eliminating trends. This can also remove seasonality, if differences are taken appropriately (e.g. differencing observations 1 year apart to remove a yearly trend). Transformations such as logarithms can help to stabilize the variance of a time series.
Stationarization by means of the surrogate method
The surrogate method for stationarization [7] works by generating a new time series that preserves certain statistical properties of the original series while removing its nonstationary components [8][9][10]. A common approach is to apply the Fourier Transform to the original time series to obtain its magnitude and phase spectra. The magnitude spectrum, which determines the power distribution across frequencies, is retained to preserve the global autocorrelation structure. The phase spectrum, which encodes the temporal alignment of frequency components and is often responsible for time-dependent dynamics in the time series (like non-stationarities), is then randomized, typically by replacing it with a set of random phases drawn uniformly from while enforcing conjugate symmetry to ensure a real-valued inverse. Applying the inverse Fourier Transform to the modified spectra yields a strictly stationary surrogate time series [11]: one with the same power spectrum as the original but lacking the temporal structures that caused non-stationarity. This technique is often used in hypothesis tests for probing the stationarity property [12][13][14][15].
See also
- Lévy process
- Stationary ergodic process
- Wiener–Khinchin theorem
- Ergodicity
- Statistical regularity
- Autocorrelation
- Whittle likelihood
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Park, Kun Il (2018). Fundamentals of Probability and Stochastic Processes with Applications to Communications. Springer. ISBN 978-3-319-68074-3.
- ↑ 2.0 2.1 Ionut Florescu (7 November 2014). Probability and Stochastic Processes. John Wiley & Sons. ISBN 978-1-118-59320-2.
- ↑ Priestley, M. B. (1981). Spectral Analysis and Time Series. Academic Press. ISBN 0-12-564922-3.
- ↑ Priestley, M. B. (1988). Non-linear and Non-stationary Time Series Analysis. Academic Press. ISBN 0-12-564911-8. https://archive.org/details/nonlinearnonstat0000prie.
- ↑ Honarkhah, M.; Caers, J. (2010). "Stochastic Simulation of Patterns Using Distance-Based Pattern Modeling". Mathematical Geosciences 42 (5): 487–517. doi:10.1007/s11004-010-9276-7. Bibcode: 2010MatGe..42..487H.
- ↑ Hyndman, Rob J.; Athanasopoulos, George. "8.1 Stationarity and differencing". Forecasting: Principles and Practice (2nd ed.). OTexts. https://www.otexts.org/fpp/8/1. Retrieved 2016-05-18.
- ↑ Pierre Borgnat and Patrick Flandrin. (2009). Stationarization via surrogates. Journal of Statistical Mechanics: Theory and Experiment, vol. 2009, n. 1, https://iopscience.iop.org/article/10.1088/1742-5468/2009/01/P01001
- ↑ Pierre Borgnat et al. (2010). Testing Stationarity With Surrogates: A Time-Frequency Approach. IEEE Transactions on Signal Processing, vol. 58, n. 7, pp. 3459-3470 https://ieeexplore.ieee.org/document/5419113
- ↑ Pierre Borgnat et al. (2011). Transitional Surrogates. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing, pp. 3600-3603 https://ieeexplore.ieee.org/document/5946257
- ↑ Douglas Baptista de Souza et al. (2019). An Improved Stationarity Test Based on Surrogates. IEEE Signal Processing Letters, vol. 26, n. 10, pp. 1431-1435 https://ieeexplore.ieee.org/abstract/document/8777090
- ↑ Cédric Richard et al. (2010). Statistical hypothesis testing with time-frequency surrogates to check signal stationarity. 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, pp. 3666-3669 https://ieeexplore.ieee.org/document/5495887
- ↑ Pierre Borgnat et al. (2010). Testing Stationarity With Surrogates: A Time-Frequency Approach. IEEE Transactions on Signal Processing, vol. 58, n. 7, pp. 3459-3470 https://ieeexplore.ieee.org/document/5419113
- ↑ Douglas Baptista de Souza et al. (2019). An Improved Stationarity Test Based on Surrogates. IEEE Signal Processing Letters, vol. 26, n. 10, pp. 1431-1435 https://ieeexplore.ieee.org/abstract/document/8777090
- ↑ Douglas Baptista de Souza et al. (2012). A modified time-frequency method for testing wide-sense stationarity. 2012 IEEE International Conference on Acoustics, Speech and Signal Processing, pp. 3409-3412 https://ieeexplore.ieee.org/abstract/document/6288648
- ↑ Jun Xiao et al. (2007). Testing Stationarity with Surrogates - A One-Class SVM Approach. 2007 IEEE/SP 14th Workshop on Statistical Signal Processing, pp. 720-724 https://ieeexplore.ieee.org/document/4301353
Further reading
- Enders, Walter (2010). Applied Econometric Time Series (Third ed.). New York: Wiley. pp. 53–57. ISBN 978-0-470-50539-7.
- Jestrovic, I.; Coyle, J. L.; Sejdic, E (2015). "The effects of increased fluid viscosity on stationary characteristics of EEG signal in healthy adults". Brain Research 1589: 45–53. doi:10.1016/j.brainres.2014.09.035. PMID 25245522.
- Hyndman, Athanasopoulos (2013). Forecasting: Principles and Practice. Otexts. https://www.otexts.org/fpp/8/1
External links
 |
 KSF
KSF