Stochastic dynamic programming

Short description: 1957 technique for modelling problems of decision making under uncertainty

Originally introduced by Richard E. Bellman in (Bellman 1957), stochastic dynamic programming is a technique for modelling and solving problems of decision making under uncertainty. Closely related to stochastic programming and dynamic programming, stochastic dynamic programming represents the problem under scrutiny in the form of a Bellman equation. The aim is to compute a policy prescribing how to act optimally in the face of uncertainty.

A motivating example: Gambling game

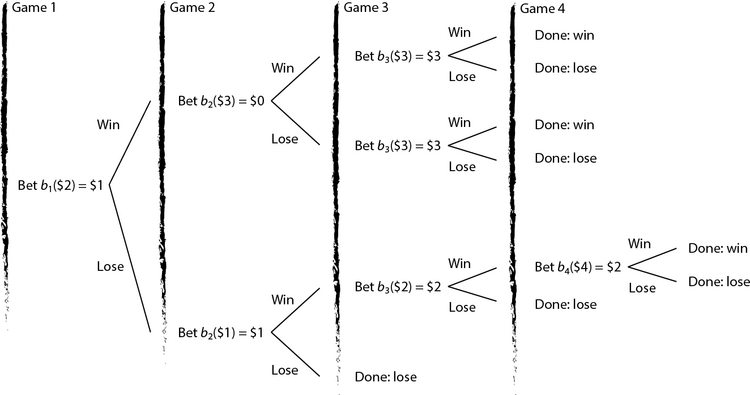
A gambler has $2, she is allowed to play a game of chance 4 times and her goal is to maximize her probability of ending up with a least $6. If the gambler bets $[math]\displaystyle{ b }[/math] on a play of the game, then with probability 0.4 she wins the game, recoup the initial bet, and she increases her capital position by $[math]\displaystyle{ b }[/math]; with probability 0.6, she loses the bet amount $[math]\displaystyle{ b }[/math]; all plays are pairwise independent. On any play of the game, the gambler may not bet more money than she has available at the beginning of that play.^[1]

Stochastic dynamic programming can be employed to model this problem and determine a betting strategy that, for instance, maximizes the gambler's probability of attaining a wealth of at least $6 by the end of the betting horizon.

Note that if there is no limit to the number of games that can be played, the problem becomes a variant of the well known St. Petersburg paradox.

An optimal betting strategy that maximizes the gambler's probability of attaining a wealth of at least $6 by the end of the betting horizon; [math]\displaystyle{ b_t(\$x) }[/math] represents the bet amount for game [math]\displaystyle{ t }[/math] when the gambler has $[math]\displaystyle{ x }[/math] at the beginning of that play. If the decision maker follows this policy, with probability 0.1984 she will attain a wealth of at least $6.

Formal background

Consider a discrete system defined on [math]\displaystyle{ n }[/math] stages in which each stage [math]\displaystyle{ t=1,\ldots,n }[/math] is characterized by

an initial state [math]\displaystyle{ s_t\in S_t }[/math], where [math]\displaystyle{ S_t }[/math] is the set of feasible states at the beginning of stage [math]\displaystyle{ t }[/math];
a decision variable [math]\displaystyle{ x_t\in X_t }[/math], where [math]\displaystyle{ X_t }[/math] is the set of feasible actions at stage [math]\displaystyle{ t }[/math] – note that [math]\displaystyle{ X_t }[/math] may be a function of the initial state [math]\displaystyle{ s_t }[/math];
an immediate cost/reward function [math]\displaystyle{ p_t(s_t,x_t) }[/math], representing the cost/reward at stage [math]\displaystyle{ t }[/math] if [math]\displaystyle{ s_t }[/math] is the initial state and [math]\displaystyle{ x_t }[/math] the action selected;
a state transition function [math]\displaystyle{ g_t(s_t,x_t) }[/math] that leads the system towards state [math]\displaystyle{ s_{t+1}=g_t(s_t,x_t) }[/math].

Let [math]\displaystyle{ f_t(s_t) }[/math] represent the optimal cost/reward obtained by following an optimal policy over stages [math]\displaystyle{ t,t+1,\ldots,n }[/math]. Without loss of generality in what follow we will consider a reward maximisation setting. In deterministic dynamic programming one usually deals with functional equations taking the following structure

[math]\displaystyle{ f_t(s_t)=\max_{x_t\in X_t}\{p_t(s_t,x_t)+f_{t+1}(s_{t+1})\} }[/math]

where [math]\displaystyle{ s_{t+1}=g_t(s_t,x_t) }[/math] and the boundary condition of the system is

[math]\displaystyle{ f_n(s_n)=\max_{x_n\in X_n}\{p_n(s_n,x_n)\}. }[/math]

The aim is to determine the set of optimal actions that maximise [math]\displaystyle{ f_1(s_1) }[/math]. Given the current state [math]\displaystyle{ s_t }[/math] and the current action [math]\displaystyle{ x_t }[/math], we know with certainty the reward secured during the current stage and – thanks to the state transition function [math]\displaystyle{ g_t }[/math] – the future state towards which the system transitions.

In practice, however, even if we know the state of the system at the beginning of the current stage as well as the decision taken, the state of the system at the beginning of the next stage and the current period reward are often random variables that can be observed only at the end of the current stage.

Stochastic dynamic programming deals with problems in which the current period reward and/or the next period state are random, i.e. with multi-stage stochastic systems. The decision maker's goal is to maximise expected (discounted) reward over a given planning horizon.

In their most general form, stochastic dynamic programs deal with functional equations taking the following structure

[math]\displaystyle{ f_t(s_t)=\max_{x_t\in X_t(s_t)} \left\{(\text{expected reward during stage } t\mid s_t,x_t) + \alpha\sum_{s_{t+1}} \Pr(s_{t+1}\mid s_t,x_t)f_{t+1}(s_{t+1})\right\} }[/math]

where

[math]\displaystyle{ f_t(s_t) }[/math] is the maximum expected reward that can be attained during stages [math]\displaystyle{ t,t+1,\ldots,n }[/math], given state [math]\displaystyle{ s_t }[/math] at the beginning of stage [math]\displaystyle{ t }[/math];
[math]\displaystyle{ x_t }[/math] belongs to the set [math]\displaystyle{ X_t(s_t) }[/math] of feasible actions at stage [math]\displaystyle{ t }[/math] given initial state [math]\displaystyle{ s_t }[/math];
[math]\displaystyle{ \alpha }[/math] is the discount factor;
[math]\displaystyle{ \Pr(s_{t+1}\mid s_t,x_t) }[/math] is the conditional probability that the state at the end of stage [math]\displaystyle{ t }[/math] is [math]\displaystyle{ s_{t+1} }[/math] given current state [math]\displaystyle{ s_t }[/math] and selected action [math]\displaystyle{ x_t }[/math].

Markov decision processes represent a special class of stochastic dynamic programs in which the underlying stochastic process is a stationary process that features the Markov property.

Gambling game as a stochastic dynamic program

Gambling game can be formulated as a Stochastic Dynamic Program as follows: there are [math]\displaystyle{ n=4 }[/math] games (i.e. stages) in the planning horizon

the state [math]\displaystyle{ s }[/math] in period [math]\displaystyle{ t }[/math] represents the initial wealth at the beginning of period [math]\displaystyle{ t }[/math];
the action given state [math]\displaystyle{ s }[/math] in period [math]\displaystyle{ t }[/math] is the bet amount [math]\displaystyle{ b }[/math];
the transition probability [math]\displaystyle{ p^a_{i,j} }[/math] from state [math]\displaystyle{ i }[/math] to state [math]\displaystyle{ j }[/math] when action [math]\displaystyle{ a }[/math] is taken in state [math]\displaystyle{ i }[/math] is easily derived from the probability of winning (0.4) or losing (0.6) a game.

Let [math]\displaystyle{ f_t(s) }[/math] be the probability that, by the end of game 4, the gambler has at least $6, given that she has $[math]\displaystyle{ s }[/math] at the beginning of game [math]\displaystyle{ t }[/math].

the immediate profit incurred if action [math]\displaystyle{ b }[/math] is taken in state [math]\displaystyle{ s }[/math] is given by the expected value [math]\displaystyle{ p_t(s,b)=0.4 f_{t+1}(s+b)+0.6 f_{t+1}(s-b) }[/math].

To derive the functional equation, define [math]\displaystyle{ b_t(s) }[/math] as a bet that attains [math]\displaystyle{ f_t(s) }[/math], then at the beginning of game [math]\displaystyle{ t=4 }[/math]

if [math]\displaystyle{ s\lt 3 }[/math] it is impossible to attain the goal, i.e. [math]\displaystyle{ f_4(s)=0 }[/math] for [math]\displaystyle{ s\lt 3 }[/math];
if [math]\displaystyle{ s\geq 6 }[/math] the goal is attained, i.e. [math]\displaystyle{ f_4(s)=1 }[/math] for [math]\displaystyle{ s\geq 6 }[/math];
if [math]\displaystyle{ 3\leq s\leq 5 }[/math] the gambler should bet enough to attain the goal, i.e. [math]\displaystyle{ f_4(s)=0.4 }[/math] for [math]\displaystyle{ 3\leq s\leq 5 }[/math].

For [math]\displaystyle{ t\lt 4 }[/math] the functional equation is [math]\displaystyle{ f_t(s)=\max_{b_t(s)}\{ 0.4 f_{t+1}(s+b)+0.6 f_{t+1}(s-b)\} }[/math], where [math]\displaystyle{ b_t(s) }[/math] ranges in [math]\displaystyle{ 0,...,s }[/math]; the aim is to find [math]\displaystyle{ f_1(2) }[/math].

Given the functional equation, an optimal betting policy can be obtained via forward recursion or backward recursion algorithms, as outlined below.

Solution methods

Stochastic dynamic programs can be solved to optimality by using backward recursion or forward recursion algorithms. Memoization is typically employed to enhance performance. However, like deterministic dynamic programming also its stochastic variant suffers from the curse of dimensionality. For this reason approximate solution methods are typically employed in practical applications.

Backward recursion

Given a bounded state space, backward recursion (Bertsekas 2000) begins by tabulating [math]\displaystyle{ f_n(k) }[/math] for every possible state [math]\displaystyle{ k }[/math] belonging to the final stage [math]\displaystyle{ n }[/math]. Once these values are tabulated, together with the associated optimal state-dependent actions [math]\displaystyle{ x_n(k) }[/math], it is possible to move to stage [math]\displaystyle{ n-1 }[/math] and tabulate [math]\displaystyle{ f_{n-1}(k) }[/math] for all possible states belonging to the stage [math]\displaystyle{ n-1 }[/math]. The process continues by considering in a backward fashion all remaining stages up to the first one. Once this tabulation process is complete, [math]\displaystyle{ f_1(s) }[/math] – the value of an optimal policy given initial state [math]\displaystyle{ s }[/math] – as well as the associated optimal action [math]\displaystyle{ x_1(s) }[/math] can be easily retrieved from the table. Since the computation proceeds in a backward fashion, it is clear that backward recursion may lead to computation of a large number of states that are not necessary for the computation of [math]\displaystyle{ f_1(s) }[/math].

Example: Gambling game

Forward recursion

Given the initial state [math]\displaystyle{ s }[/math] of the system at the beginning of period 1, forward recursion (Bertsekas 2000) computes [math]\displaystyle{ f_1(s) }[/math] by progressively expanding the functional equation (forward pass). This involves recursive calls for all [math]\displaystyle{ f_{t+1}(\cdot), f_{t+2}(\cdot), \ldots }[/math] that are necessary for computing a given [math]\displaystyle{ f_t(\cdot) }[/math]. The value of an optimal policy and its structure are then retrieved via a (backward pass) in which these suspended recursive calls are resolved. A key difference from backward recursion is the fact that [math]\displaystyle{ f_t }[/math] is computed only for states that are relevant for the computation of [math]\displaystyle{ f_1(s) }[/math]. Memoization is employed to avoid recomputation of states that have been already considered.

Example: Gambling game

We shall illustrate forward recursion in the context of the Gambling game instance previously discussed. We begin the forward pass by considering [math]\displaystyle{ f_1(2)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 1,2,3,4}\\ \hline 0&0.4f_{2}(2+0)+0.6f_{2}(2-0)\\ 1&0.4f_{2}(2+1)+0.6f_{2}(2-1)\\ 2&0.4f_{2}(2+2)+0.6f_{2}(2-2)\\ \end{array} \right. }[/math]

At this point we have not computed yet [math]\displaystyle{ f_{2}(4),f_{2}(3), f_{2}(2), f_{2}(1), f_{2}(0) }[/math], which are needed to compute [math]\displaystyle{ f_1(2) }[/math]; we proceed and compute these items. Note that [math]\displaystyle{ f_{2}(2+0)= f_{2}(2-0)=f_{2}(2) }[/math], therefore one can leverage memoization and perform the necessary computations only once.

Computation of [math]\displaystyle{ f_{2}(4),f_{2}(3), f_{2}(2), f_{2}(1), f_{2}(0) }[/math]

[math]\displaystyle{ f_2(0)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 2,3,4}\\ \hline 0&0.4f_{3}(0+0)+0.6f_{3}(0-0)\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_2(1)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 2,3,4}\\ \hline 0&0.4f_{3}(1+0)+0.6f_{3}(1-0)\\ 1&0.4f_{3}(1+1)+0.6f_{3}(1-1)\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_2(2)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 2,3,4}\\ \hline 0&0.4f_{3}(2+0)+0.6f_{3}(2-0)\\ 1&0.4f_{3}(2+1)+0.6f_{3}(2-1)\\ 2&0.4f_{3}(2+2)+0.6f_{3}(2-2)\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_2(3)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 2,3,4}\\ \hline 0&0.4f_{3}(3+0)+0.6f_{3}(3-0)\\ 1&0.4f_{3}(3+1)+0.6f_{3}(3-1)\\ 2&0.4f_{3}(3+2)+0.6f_{3}(3-2)\\ 3&0.4f_{3}(3+3)+0.6f_{3}(3-3)\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_2(4)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 2,3,4}\\ \hline 0&0.4f_{3}(4+0)+0.6f_{3}(4-0)\\ 1&0.4f_{3}(4+1)+0.6f_{3}(4-1)\\ 2&0.4f_{3}(4+2)+0.6f_{3}(4-2) \end{array} \right. }[/math]

We have now computed [math]\displaystyle{ f_2(k) }[/math] for all [math]\displaystyle{ k }[/math] that are needed to compute [math]\displaystyle{ f_1(2) }[/math]. However, this has led to additional suspended recursions involving [math]\displaystyle{ f_{3}(4), f_{3}(3), f_{3}(2), f_{3}(1), f_{3}(0) }[/math]. We proceed and compute these values.

Computation of [math]\displaystyle{ f_{3}(4), f_{3}(3), f_{3}(2), f_{3}(1), f_{3}(0) }[/math]

[math]\displaystyle{ f_3(0)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 3,4}\\ \hline 0&0.4f_{4}(0+0)+0.6f_{4}(0-0)\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_3(1)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 3,4}\\ \hline 0&0.4f_{4}(1+0)+0.6f_{4}(1-0)\\ 1&0.4f_{4}(1+1)+0.6f_{4}(1-1)\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_3(2)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 3,4}\\ \hline 0&0.4f_{4}(2+0)+0.6f_{4}(2-0)\\ 1&0.4f_{4}(2+1)+0.6f_{4}(2-1)\\ 2&0.4f_{4}(2+2)+0.6f_{4}(2-2)\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_3(3)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 3,4}\\ \hline 0&0.4f_{4}(3+0)+0.6f_{4}(3-0)\\ 1&0.4f_{4}(3+1)+0.6f_{4}(3-1)\\ 2&0.4f_{4}(3+2)+0.6f_{4}(3-2)\\ 3&0.4f_{4}(3+3)+0.6f_{4}(3-3)\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_3(4)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 3,4}\\ \hline 0&0.4f_{4}(4+0)+0.6f_{4}(4-0)\\ 1&0.4f_{4}(4+1)+0.6f_{4}(4-1)\\ 2&0.4f_{4}(4+2)+0.6f_{4}(4-2) \end{array} \right. }[/math]

[math]\displaystyle{ f_3(5)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 3,4}\\ \hline 0&0.4f_{4}(5+0)+0.6f_{4}(5-0)\\ 1&0.4f_{4}(5+1)+0.6f_{4}(5-1) \end{array} \right. }[/math]

Since stage 4 is the last stage in our system, [math]\displaystyle{ f_{4}(\cdot) }[/math] represent boundary conditions that are easily computed as follows.

Boundary conditions

[math]\displaystyle{ \begin{array}{ll} f_4(0)=0&b_4(0)=0\\ f_4(1)=0&b_4(1)=\{0,1\}\\ f_4(2)=0&b_4(2)=\{0,1,2\}\\ f_4(3)=0.4&b_4(3)=\{3\}\\ f_4(4)=0.4&b_4(4)=\{2,3,4\}\\ f_4(5)=0.4&b_4(5)=\{1,2,3,4,5\}\\ f_4(d)=1&b_4(d)=\{0,\ldots,d-6\}\text{ for }d\geq 6 \end{array} }[/math]

At this point it is possible to proceed and recover the optimal policy and its value via a backward pass involving, at first, stage 3

Backward pass involving [math]\displaystyle{ f_3(\cdot) }[/math]

[math]\displaystyle{ f_3(0)= \min\left\{ \begin{array}{rr} b&\text{success probability in periods 3,4}\\ \hline 0&0.4(0)+0.6(0)=0\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_3(1)= \min\left\{ \begin{array}{rrr} b&\text{success probability in periods 3,4}&\mbox{max}\\ \hline 0&0.4(0)+0.6(0)=0&\leftarrow b_3(1)=0\\ 1&0.4(0)+0.6(0)=0&\leftarrow b_3(1)=1\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_3(2)= \min\left\{ \begin{array}{rrr} b&\text{success probability in periods 3,4}&\mbox{max}\\ \hline 0&0.4(0)+0.6(0)=0\\ 1&0.4(0.4)+0.6(0)=0.16&\leftarrow b_3(2)=1\\ 2&0.4(0.4)+0.6(0)=0.16&\leftarrow b_3(2)=2\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_3(3)= \min\left\{ \begin{array}{rrr} b&\text{success probability in periods 3,4}&\mbox{max}\\ \hline 0&0.4(0.4)+0.6(0.4)=0.4&\leftarrow b_3(3)=0\\ 1&0.4(0.4)+0.6(0)=0.16\\ 2&0.4(0.4)+0.6(0)=0.16\\ 3&0.4(1)+0.6(0)=0.4&\leftarrow b_3(3)=3\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_3(4)= \min\left\{ \begin{array}{rrr} b&\text{success probability in periods 3,4}&\mbox{max}\\ \hline 0&0.4(0.4)+0.6(0.4)=0.4&\leftarrow b_3(4)=0\\ 1&0.4(0.4)+0.6(0.4)=0.4&\leftarrow b_3(4)=1\\ 2&0.4(1)+0.6(0)=0.4&\leftarrow b_3(4)=2\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_3(5)= \min\left\{ \begin{array}{rrr} b&\text{success probability in periods 3,4}&\mbox{max}\\ \hline 0&0.4(0.4)+0.6(0.4)=0.4\\ 1&0.4(1)+0.6(0.4)=0.64&\leftarrow b_3(5)=1\\ \end{array} \right. }[/math]

and, then, stage 2.

Backward pass involving [math]\displaystyle{ f_2(\cdot) }[/math]

[math]\displaystyle{ f_2(0)= \min\left\{ \begin{array}{rrr} b&\text{success probability in periods 2,3,4}&\mbox{max}\\ \hline 0&0.4(0)+0.6(0)=0&\leftarrow b_2(0)=0\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_2(1)= \min\left\{ \begin{array}{rrr} b&\text{success probability in periods 2,3,4}&\mbox{max}\\ \hline 0&0.4(0)+0.6(0)=0\\ 1&0.4(0.16)+0.6(0)=0.064&\leftarrow b_2(1)=1\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_2(2)= \min\left\{ \begin{array}{rrr} b&\text{success probability in periods 2,3,4}&\mbox{max}\\ \hline 0&0.4(0.16)+0.6(0.16)=0.16&\leftarrow b_2(2)=0\\ 1&0.4(0.4)+0.6(0)=0.16&\leftarrow b_2(2)=1\\ 2&0.4(0.4)+0.6(0)=0.16&\leftarrow b_2(2)=2\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_2(3)= \min\left\{ \begin{array}{rrr} b&\text{success probability in periods 2,3,4}&\mbox{max}\\ \hline 0&0.4(0.4)+0.6(0.4)=0.4&\leftarrow b_2(3)=0\\ 1&0.4(0.4)+0.6(0.16)=0.256\\ 2&0.4(0.64)+0.6(0)=0.256\\ 3&0.4(1)+0.6(0)=0.4&\leftarrow b_2(3)=3\\ \end{array} \right. }[/math]

[math]\displaystyle{ f_2(4)= \min\left\{ \begin{array}{rrr} b&\text{success probability in periods 2,3,4}&\mbox{max}\\ \hline 0&0.4(0.4)+0.6(0.4)=0.4\\ 1&0.4(0.64)+0.6(0.4)=0.496&\leftarrow b_2(4)=1\\ 2&0.4(1)+0.6(0.16)=0.496&\leftarrow b_2(4)=2\\ \end{array} \right. }[/math]

We finally recover the value [math]\displaystyle{ f_1(2) }[/math] of an optimal policy

[math]\displaystyle{ f_1(2)= \min\left\{ \begin{array}{rrr} b&\text{success probability in periods 1,2,3,4}&\mbox{max}\\ \hline 0&0.4(0.16)+0.6(0.16)=0.16\\ 1&0.4(0.4)+0.6(0.064)=0.1984&\leftarrow b_1(2)=1\\ 2&0.4(0.496)+0.6(0)=0.1984&\leftarrow b_1(2)=2\\ \end{array} \right. }[/math]

This is the optimal policy that has been previously illustrated. Note that there are multiple optimal policies leading to the same optimal value [math]\displaystyle{ f_1(2)=0.1984 }[/math]; for instance, in the first game one may either bet $1 or $2.

Python implementation. The one that follows is a complete Python implementation of this example.

from typing import List, Tuple
import memoize as mem
import functools


class memoize:
    def __init__(self, func):
        self.func = func
        self.memoized = {}
        self.method_cache = {}

    def __call__(self, *args):
        return self.cache_get(self.memoized, args, lambda: self.func(*args))

    def __get__(self, obj, objtype):
        return self.cache_get(
            self.method_cache,
            obj,
            lambda: self.__class__(functools.partial(self.func, obj)),
        )

    def cache_get(self, cache, key, func):
        try:
            return cache[key]
        except KeyError:
            cache[key] = func()
            return cache[key]

    def reset(self):
        self.memoized = {}
        self.method_cache = {}


class State:
    """the state of the gambler's ruin problem"""

    def __init__(self, t: int, wealth: float):
        """state constructor

        Arguments:
            t {int} -- time period
            wealth {float} -- initial wealth
        """
        self.t, self.wealth = t, wealth

    def __eq__(self, other):
        return self.__dict__ == other.__dict__

    def __str__(self):
        return str(self.t) + " " + str(self.wealth)

    def __hash__(self):
        return hash(str(self))


class GamblersRuin:
    def __init__(
        self,
        bettingHorizon: int,
        targetWealth: float,
        pmf: List[List[Tuple[int, float]]],
    ):
        """the gambler's ruin problem

        Arguments:
            bettingHorizon {int} -- betting horizon
            targetWealth {float} -- target wealth
            pmf {List[List[Tuple[int, float]]]} -- probability mass function
        """

        # initialize instance variables
        self.bettingHorizon, self.targetWealth, self.pmf = (
            bettingHorizon,
            targetWealth,
            pmf,
        )

        # lambdas
        self.ag = lambda s: [
            i for i in range(0, min(self.targetWealth // 2, s.wealth) + 1)
        ]  # action generator
        self.st = lambda s, a, r: State(
            s.t + 1, s.wealth - a + a * r
        )  # state transition
        self.iv = (
            lambda s, a, r: 1 if s.wealth - a + a * r >= self.targetWealth else 0
        )  # immediate value function

        self.cache_actions = {}  # cache with optimal state/action pairs

    def f(self, wealth: float) -> float:
        s = State(0, wealth)
        return self._f(s)

    def q(self, t: int, wealth: float) -> float:
        s = State(t, wealth)
        return self.cache_actions[str(s)]

    @memoize
    def _f(self, s: State) -> float:
        # Forward recursion
        v = max(
            [
                sum(
                    [
                        p[1]
                        * (
                            self._f(self.st(s, a, p[0]))
                            if s.t < self.bettingHorizon - 1
                            else self.iv(s, a, p[0])
                        )  # future value
                        for p in self.pmf[s.t]
                    ]
                )  # random variable realisations
                for a in self.ag(s)
            ]
        )  # actions

        opt_a = (
            lambda a: sum(
                [
                    p[1]
                    * (
                        self._f(self.st(s, a, p[0]))
                        if s.t < self.bettingHorizon - 1
                        else self.iv(s, a, p[0])
                    )
                    for p in self.pmf[s.t]
                ]
            )
            == v
        )
        q = [k for k in filter(opt_a, self.ag(s))]  # retrieve best action list
        self.cache_actions[str(s)] = (
            q[0] if bool(q) else None
        )  # store an action in dictionary

        return v  # return value


instance = {
    "bettingHorizon": 4,
    "targetWealth": 6,
    "pmf": [[(0, 0.6), (2, 0.4)] for i in range(0, 4)],
}
gr, initial_wealth = GamblersRuin(**instance), 2

# f_1(x) is gambler's probability of attaining $targetWealth at the end of bettingHorizon
print("f_1(" + str(initial_wealth) + "): " + str(gr.f(initial_wealth)))

# Recover optimal action for period 2 when initial wealth at the beginning of period 2 is $1.
t, initial_wealth = 1, 1
print(
    "b_" + str(t + 1) + "(" + str(initial_wealth) + "): " + str(gr.q(t, initial_wealth))
)

Java implementation. GamblersRuin.java is a standalone Java 8 implementation of the above example.

Approximate dynamic programming

An introduction to approximate dynamic programming is provided by (Powell 2009).

References

↑ This problem is adapted from W. L. Winston, Operations Research: Applications and Algorithms (7th Edition), Duxbury Press, 2003, chap. 19, example 3.

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Stochastic dynamic programming. Read more

[1] This problem is adapted from W. L. Winston, Operations Research: Applications and Algorithms (7th Edition), Duxbury Press, 2003, chap. 19, example 3.

[1]

Stochastic dynamic programming

Contents

A motivating example: Gambling game

Formal background

Gambling game as a stochastic dynamic program

Solution methods

Backward recursion

Example: Gambling game

Forward recursion

Example: Gambling game

Approximate dynamic programming

Further reading

See also

References