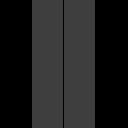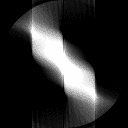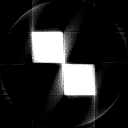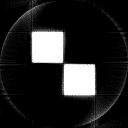Table of Contents Categories
  Encyclosphere.org ENCYCLOREADER
  supported by EncyclosphereKSF

Tomographic reconstruction

From HandWiki - Reading time: 11 min
Short description: Estimate object properties from a finite number of projections

File:Tomographic reconstruction- Projection, Back projection and Filtered back projection.webm Tomographic reconstruction is a type of multidimensional inverse problem where the challenge is to yield an estimate of a specific system from a finite number of projections. The mathematical basis for tomographic imaging was laid down by Johann Radon. A notable example of applications is the reconstruction of computed tomography (CT) where cross-sectional images of patients are obtained in non-invasive manner. Recent developments have seen the Radon transform and its inverse used for tasks related to realistic object insertion required for testing and evaluating computed tomography use in airport security.[1]

This article applies in general to reconstruction methods for all kinds of tomography, but some of the terms and physical descriptions refer directly to the reconstruction of X-ray computed tomography.

Introducing formula

Figure 1: Parallel beam geometry utilized in tomography and tomographic reconstruction. Each projection, resulting from tomography under a specific angle, is made up of the set of line integrals through the object.
Resulting tomographic image from a plastic skull phantom. Projected X-rays are clearly visible on this slice taken with a CT-scan as image artifacts, due to limited amount of projection slices over angles.

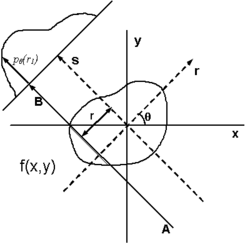
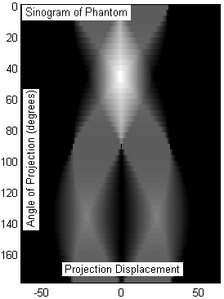
The projection of an object, resulting from the tomographic measurement process at a given angle [math]\displaystyle{ \theta }[/math], is made up of a set of line integrals (see Fig. 1). A set of many such projections under different angles organized in 2D is called sinogram (see Fig. 3). In X-ray CT, the line integral represents the total attenuation of the beam of x-rays as it travels in a straight line through the object. As mentioned above, the resulting image is a 2D (or 3D) model of the attenuation coefficient. That is, we wish to find the image [math]\displaystyle{ \mu(x,y) }[/math]. The simplest and easiest way to visualise the method of scanning is the system of parallel projection, as used in the first scanners. For this discussion we consider the data to be collected as a series of parallel rays, at position [math]\displaystyle{ r }[/math], across a projection at angle [math]\displaystyle{ \theta }[/math]. This is repeated for various angles. Attenuation occurs exponentially in tissue:

[math]\displaystyle{ I = I_0\exp\left({-\int\mu(x,y)\,ds}\right) }[/math]

where [math]\displaystyle{ \mu(x,y) }[/math] is the attenuation coefficient as a function of position. Therefore, generally the total attenuation [math]\displaystyle{ p }[/math] of a ray at position [math]\displaystyle{ r }[/math], on the projection at angle [math]\displaystyle{ \theta }[/math], is given by the line integral:

[math]\displaystyle{ p_{\theta}(r) = \ln \left(\frac{I}{I_0}\right) = -\int\mu(x,y)\,ds }[/math]

Using the coordinate system of Figure 1, the value of [math]\displaystyle{ r }[/math] onto which the point [math]\displaystyle{ (x,y) }[/math] will be projected at angle [math]\displaystyle{ \theta }[/math] is given by:

[math]\displaystyle{ x\cos\theta + y\sin\theta = r\ }[/math]

So the equation above can be rewritten as

[math]\displaystyle{ p_{\theta}(r)=\int^\infty_{-\infty}\int^\infty_{-\infty}f(x,y)\delta(x\cos\theta+y\sin\theta-r)\,dx\,dy }[/math]

where [math]\displaystyle{ f(x,y) }[/math] represents [math]\displaystyle{ \mu(x,y) }[/math] and [math]\displaystyle{ \delta() }[/math] is the Dirac delta function. This function is known as the Radon transform (or sinogram) of the 2D object.

The Fourier Transform of the projection can be written as

[math]\displaystyle{ P_\theta(\omega)=\int^\infty_{-\infty}\int^\infty_{-\infty}f(x,y)\exp[-j\omega(x\cos\theta+y\sin\theta)]\,dx\,dy = F(\Omega_1,\Omega_2) }[/math] where [math]\displaystyle{ \Omega_1 =\omega\cos\theta, \Omega_2 =\omega\sin\theta }[/math][2]

[math]\displaystyle{ P_\theta(\omega) }[/math] represents a slice of the 2D Fourier transform of [math]\displaystyle{ f(x,y) }[/math] at angle [math]\displaystyle{ \theta }[/math]. Using the inverse Fourier transform, the inverse Radon transform formula can be easily derived.

[math]\displaystyle{ f(x,y) = \frac{1}{2\pi} \int\limits_{0}^{\pi} g_\theta(x\cos\theta+y\sin\theta)d\theta }[/math]

where [math]\displaystyle{ g_\theta(x\cos\theta+y\sin\theta) }[/math] is the derivative of the Hilbert transform of [math]\displaystyle{ p_{\theta}(r) }[/math]

In theory, the inverse Radon transformation would yield the original image. The projection-slice theorem tells us that if we had an infinite number of one-dimensional projections of an object taken at an infinite number of angles, we could perfectly reconstruct the original object, [math]\displaystyle{ f(x,y) }[/math]. However, there will only be a finite number of projections available in practice.

Assuming [math]\displaystyle{ f(x,y) }[/math] has effective diameter [math]\displaystyle{ d }[/math] and desired resolution is [math]\displaystyle{ R_s }[/math], rule of thumb number of projections needed for reconstruction is [math]\displaystyle{ N \gt \pi d / R_s }[/math][2]

Reconstruction algorithms

Practical reconstruction algorithms have been developed to implement the process of reconstruction of a three-dimensional object from its projections.[3][2] These algorithms are designed largely based on the mathematics of the Radon transform, statistical knowledge of the data acquisition process and geometry of the data imaging system.

Fourier-domain reconstruction algorithm

Reconstruction can be made using interpolation. Assume [math]\displaystyle{ N }[/math] projections of [math]\displaystyle{ f(x,y) }[/math] are generated at equally spaced angles, each sampled at the same rate. The discrete Fourier transform (DFT) on each projection yields sampling in the frequency domain. Combining all the frequency-sampled projections generates a polar raster in the frequency domain. The polar raster is sparse, so interpolation is used to fill the unknown DFT points, and reconstruction can be done through the inverse discrete Fourier transform.[4] Reconstruction performance may improve by designing methods to change the sparsity of the polar raster, facilitating the effectiveness of interpolation.

For instance, a concentric square raster in the frequency domain can be obtained by changing the angle between each projection as follow:

[math]\displaystyle{ \theta' = \frac{R_0}{ \max\{|\cos\theta|, |\sin\theta|\}} }[/math]

where [math]\displaystyle{ R_0 }[/math] is highest frequency to be evaluated.

The concentric square raster improves computational efficiency by allowing all the interpolation positions to be on rectangular DFT lattice. Furthermore, it reduces the interpolation error.[4] Yet, the Fourier-Transform algorithm has a disadvantage of producing inherently noisy output.

Back projection algorithm

In practice of tomographic image reconstruction, often a stabilized and discretized version of the inverse Radon transform is used, known as the filtered back projection algorithm.[2]

With a sampled discrete system, the inverse Radon transform is

[math]\displaystyle{ f(x,y) = \frac{1}{2\pi} \sum_{i=0}^{N-1}\Delta\theta_i g_{\theta_i}(x\cos\theta_i+y\sin\theta_i) }[/math]

[math]\displaystyle{ g_\theta(t) = p_\theta(t) \cdot k(t) }[/math]

where [math]\displaystyle{ \Delta\theta }[/math] is the angular spacing between the projections and [math]\displaystyle{ k(t) }[/math] is a Radon kernel with frequency response [math]\displaystyle{ |\omega| }[/math].

The name back-projection comes from the fact that a one-dimensional projection needs to be filtered by a one-dimensional Radon kernel (back-projected) in order to obtain a two-dimensional signal. The filter used does not contain DC gain, so adding DC bias may be desirable. Reconstruction using back-projection allows better resolution than interpolation method described above. However, it induces greater noise because the filter is prone to amplify high-frequency content.

Iterative reconstruction algorithm

Main page: Iterative reconstruction

The iterative algorithm is computationally intensive but it allows the inclusion of a priori information about the system [math]\displaystyle{ f(x,y) }[/math].[2]

Let [math]\displaystyle{ N }[/math] be the number of projections and [math]\displaystyle{ D_i }[/math] be the distortion operator for the [math]\displaystyle{ i }[/math]th projection taken at an angle [math]\displaystyle{ \theta_i }[/math]. [math]\displaystyle{ \{\lambda_i\} }[/math] are a set of parameters to optimize the conversion of iterations.

[math]\displaystyle{ f_0(x,y) = \sum_{i=1}^N \lambda_i p_{\theta_i}(r) }[/math]

A fan-beam reconstruction of Shepp-Logan Phantom with different sensor spacing. Smaller spacing between the sensors allow finer reconstruction. The figure was generated by using MATLAB.

[math]\displaystyle{ f_k(x,y) = f_{k-1} (x,y) + \sum_{i=1}^N \lambda_i [p_{\theta_i}(r)-D_if_{k-1}(x,y)] }[/math]

An alternative family of recursive tomographic reconstruction algorithms are the algebraic reconstruction techniques and iterative sparse asymptotic minimum variance.

Fan-beam reconstruction

Use of a noncollimated fan beam is common since a collimated beam of radiation is difficult to obtain. Fan beams will generate series of line integrals, not parallel to each other, as projections. The fan-beam system requires a 360-degree range of angles, which imposes mechanical constraints, but it allows faster signal acquisition time, which may be advantageous in certain settings such as in the field of medicine. Back projection follows a similar two-step procedure that yields reconstruction by computing weighted sum back-projections obtained from filtered projections.

Deep learning reconstruction

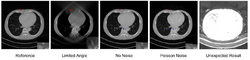
The influence of Poisson noise in deep learning reconstruction where Poisson noise causes the U-Net fail to reconstruct an existing high contrast lesion-like object.

Deep learning methods are widely applied to image reconstruction nowadays and have achieved impressive results in various image reconstruction tasks, including low-dose denoising, sparse-view reconstruction, limited angle tomography and metal artifact reduction. An excellent overview can be found in the special issue [5] of IEEE Transaction on Medical Imaging. One group of deep learning reconstruction algorithms apply post-processing neural networks to achieve image-to-image reconstruction, where input images are reconstructed by conventional reconstruction methods. Artifact reduction using the U-Net in limited angle tomography is such an example application.[6] However, incorrect structures may occur in an image reconstructed by such a completely data-driven method,[7] as displayed in the figure. Therefore, integration of known operators into the architecture design of neural networks appears beneficial, as described in the concept of precision learning.[8] For example, direct image reconstruction from projection data can be learnt from the framework of filtered back-projection.[9] Another example is to build neural networks by unrolling iterative reconstruction algorithms.[10] Except for precision learning, using conventional reconstruction methods with deep learning reconstruction prior [11] is also an alternative approach to improve the image quality of deep learning reconstruction.

Tomographic reconstruction software

For flexible tomographic reconstruction, open source toolboxes are available, such as PYRO-NN,[12] TomoPy,[13] CONRAD,[14] ODL, the ASTRA toolbox,[15][16] and TIGRE.[17] TomoPy is an open-source Python toolbox to perform tomographic data processing and image reconstruction tasks at the Advanced Photon Source at Argonne National Laboratory. TomoPy toolbox is specifically designed to be easy to use and deploy at a synchrotron facility beamline. It supports reading many common synchrotron data formats from disk through Scientific Data Exchange,[18] and includes several other processing algorithms commonly used for synchrotron data. TomoPy also includes several reconstruction algorithms, which can be run on multi-core workstations and large-scale computing facilities.[19] The ASTRA Toolbox is a MATLAB and Python toolbox of high-performance GPU primitives for 2D and 3D tomography, from 2009 to 2014 developed by iMinds-Vision Lab, University of Antwerp and since 2014 jointly developed by iMinds-VisionLab (now imec-VisionLab), UAntwerpen and CWI, Amsterdam. The toolbox supports parallel, fan, and cone beam, with highly flexible source/detector positioning. A large number of reconstruction algorithms are available through TomoPy and the ASTRA toolkit, including FBP, Gridrec, ART, SIRT, SART, BART, CGLS, PML, MLEM and OSEM. In 2016, the ASTRA toolbox has been integrated in the TomoPy framework.[20] By integrating the ASTRA toolbox in the TomoPy framework, the optimized GPU-based reconstruction methods become easily available for synchrotron beamline users, and users of the ASTRA toolbox can more easily read data and use TomoPy's other functionality for data filtering and artifact correction.

Gallery

Shown in the gallery is the complete process for a simple object tomography and the following tomographic reconstruction based on ART.

  • Fig. 2: Phantom object, two kitty-corner squares.

  • Fig. 3: Sinogram of the phantom object (Fig.2) resulting from tomography. 50 projection slices were taken over 180 degree angle, equidistantly sampled (only by coincidence the x-axis marks displacement at -50/50 units).

  • Fig.4: ART based tomographic reconstruction of the sinogram of Fig.3, presented as animation over the iterative reconstruction process. The original object could be approximatively reconstructed, as the resulting image has some visual artifacts.

See also

References

  1. ↑ Megherbi, N., Breckon, T.P., Flitton, G.T., Mouton, A. (October 2013). "Radon Transform based Metal Artefacts Generation in 3D Threat Image Projection". Proc. SPIE Optics and Photonics for Counterterrorism, Crime Fighting and Defence. 8901. SPIE. pp. 1–7. doi:10.1117/12.2028506. http://breckon.eu/toby/publications/papers/megherbi13radon.pdf. Retrieved 5 November 2013. 
  2. ↑ 2.0 2.1 2.2 2.3 2.4 Dudgeon and Mersereau (1984). Multidimensional digital signal processing. Prentice-Hall. 
  3. ↑ Herman, G. T., Fundamentals of computerized tomography: Image reconstruction from projection, 2nd edition, Springer, 2009
  4. ↑ 4.0 4.1 R. Mersereau, A. Oppenheim (1974). "Digital reconstruction of multidimensional signals from their projections". Proceedings of the IEEE 62 (10): 1319–1338. doi:10.1109/proc.1974.9625. 
  5. ↑ Wang, Ge and Ye, Jong Chu and Mueller, Klaus and Fessler, Jeffrey A (2018). "Image reconstruction is a new frontier of machine learning". IEEE Transactions on Medical Imaging 37 (6): 1289–1296. doi:10.1109/TMI.2018.2833635. PMID 29870359. 
  6. ↑ Gu, Jawook and Ye, Jong Chul (2017). "Multi-scale wavelet domain residual learning for limited-angle CT reconstruction". Fully3D. pp. 443–447. 
  7. ↑ Huang Y., Würfl T., Breininger K., Liu L., Lauritsch G., Maier A. (2018). "Some Investigations on Robustness of Deep Learning in Limited Angle Tomography". MICCAI. doi:10.1007/978-3-030-00928-1_17. 
  8. ↑ Maier, Andreas K and Syben, Christopher and Stimpel, Bernhard and Wuerfl, Tobias and Hoffmann, Mathis and Schebesch, Frank and Fu, Weilin and Mill, Leonid and Kling, Lasse and Christiansen, Silke (2019). "Learning with known operators reduces maximum error bounds". Nature Machine Intelligence 1 (8): 373–380. doi:10.1038/s42256-019-0077-5. PMID 31406960. 
  9. ↑ Tobias Wuerfl and Mathis Hoffmann and Vincent Christlein and Katharina Breininger and Yixing Huang and Mathias Unberath and Andreas Maier (2018). "Deep Learning Computed Tomography: Learning Projection-Domain Weights from Image Domain in Limited Angle Problems". IEEE Transactions on Medical Imaging 37 (6): 1454–1463. doi:10.1109/TMI.2018.2833499. PMID 29870373. 
  10. ↑ J. Adler and O. Öktem (2018). "Learned Primal-Dual Reconstruction". IEEE Transactions on Medical Imaging 37 (6): 1322–1332. doi:10.1109/TMI.2018.2799231. PMID 29870362. 
  11. ↑ Huang Y., Preuhs A., Lauritsch G., Manhart M., Huang X., Maier A. (2019). "Data Consistent Artifact Reduction for Limited Angle Tomography with Deep Learning Prior". Machine Learning for Medical Image Reconstruction. doi:10.1007/978-3-030-33843-5_10. 
  12. ↑ Syben, Christopher; Michen, Markus; Stimpel, Bernhard; Seitz, Stephan; Ploner, Stefan; Maier, Andreas (2019). "PYRO-NN: Python Reconstruction Operators in Neural Networks". Medical Physics 46 (11): 5110–5115. doi:10.1002/mp.13753. PMID 31389023. Bibcode: 2019MedPh..46.5110S. 
  13. ↑ Gursoy D, De Carlo F, Xiao X, and Jacobsen C (2014). "TomoPy: A framework for the analysis of synchrotron tomographic data". Journal of Synchrotron Radiation 22 (5): 1188–1193. doi:10.1107/S1600577514013939. PMID 25178011. Bibcode: 2014SPIE.9212E..0NG. 
  14. ↑ A. Maier, H. G. Hofmann, M. Berger, P. Fischer, C. Schwemmer, H. Wu, K. Mueller, J. Hornegger, J. Choi, C. Riess, A. Keil, A. Farhig (2013). "CONRAD - A software framework for cone-beam imaging in radiology". Medical Physics 40 (11): 111914. doi:10.1118/1.4824926. PMID 24320447. Bibcode: 2013MedPh..40k1914M. 
  15. ↑ Van Aarle, W., Palenstijn, W.J., De Beenhouwer, J., Altantzis T., Bals S., Batenburg K. J., and J. Sijbers (October 2015). "The ASTRA Toolbox: a platform for advanced algorithm development in electron tomography". Ultramicroscopy 157: 35–47. doi:10.1016/j.ultramic.2015.05.002. PMID 26057688. https://ir.cwi.nl/pub/23858. 
  16. ↑ W. Van Aarle, W J. Palenstijn, J. Cant, E. Janssens, F. Bleichrodt, A. Dabravolski, J. De Beenhouwer, K. J. Batenburg, and J. Sijbers (2016). "Fast and flexible X-ray tomography using the ASTRA toolbox". Optics Express 24 (22): 35–47. doi:10.1364/OE.24.025129. PMID 27828452. Bibcode: 2016OExpr..2425129V. https://ir.cwi.nl/pub/24770. 
  17. ↑ Released by the University of Bath and CERN.
    Biguri, Ander; Dosanjh, Manjit; Hancock, Steven; Soleimani, Manuchehr (2016-09-08). "TIGRE: a MATLAB-GPU toolbox for CBCT image reconstruction". Biomedical Physics & Engineering Express 2 (5): 055010. doi:10.1088/2057-1976/2/5/055010. ISSN 2057-1976. 
  18. ↑ De Carlo F, Gursoy D, Marone F, Rivers M, Parkinson YD, Khan F, Schwarz N, Vine DJ, Vogt S, Gleber SC, Narayanan S, Newville M, Lanzirotti T, Sun Y, Hong YP, Jacobsen C (2014). "Scientific Data Exchange: a schema for HDF5-based storage of raw and analyzed data". Journal of Synchrotron Radiation 22 (6): 35–47. doi:10.1107/S160057751401604X. PMID 25343788. Bibcode: 2014JSynR..21.1224D. https://www.dora.lib4ri.ch/psi/islandora/object/psi%3A9437. 
  19. ↑ Bicer T, Gursoy D, Kettimuthu R, De Carlo F, and Foster I (2016). "Optimization of tomographic reconstruction workflows on geographically distributed resources". Journal of Synchrotron Radiation 23 (4): 997–1005. doi:10.1107/S1600577516007980. PMID 27359149. Bibcode: 2016JSynR..23..997B. 
  20. ↑ Pelt DM, Gursoy D, Batenburg KJ, De Carlo F, Palenstijna WJ, and Sijbers J (2016). "Integration of TomoPy and the ASTRA toolbox for advanced processing and reconstruction of tomographic synchrotron data". Journal of Synchrotron Radiation 23 (3): 842–849. doi:10.1107/S1600577516005658. PMID 27140167. Bibcode: 2016JSynR..23..842P. 

Further reading

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Tomographic_reconstruction&oldid=3382910"
Licensed under CC BY-SA 3.0 | Source: https://handwiki.org/wiki/Tomographic_reconstruction
18 views | Status: cached on July 29 2024 19:21:01
↧ Download this article as ZWI file
Encyclosphere.org EncycloReader is supported by the EncyclosphereKSF