Trachtenberg system

The Trachtenberg system is a system of rapid mental calculation. The system consists of a number of readily memorized operations that allow one to perform arithmetic computations very quickly. It was developed by the Russian engineer Jakow Trachtenberg in order to keep his mind occupied while being in a Nazi concentration camp.

The rest of this article presents some methods devised by Trachtenberg. Some of the algorithms Trachtenberg developed are ones for general multiplication, division and addition. Also, the Trachtenberg system includes some specialised methods for multiplying small numbers between 5 and 13 (but shown here is 2–12).

The section on addition demonstrates an effective method of checking calculations that can also be applied to multiplication.

General multiplication

The method for general multiplication is a method to achieve multiplications [math]\displaystyle{ a\times b }[/math] with low space complexity, i.e. as few temporary results as possible to be kept in memory. This is achieved by noting that the final digit is completely determined by multiplying the last digit of the multiplicands. This is held as a temporary result. To find the next to last digit, we need everything that influences this digit: The temporary result, the last digit of [math]\displaystyle{ a }[/math] times the next-to-last digit of [math]\displaystyle{ b }[/math], as well as the next-to-last digit of [math]\displaystyle{ a }[/math] times the last digit of [math]\displaystyle{ b }[/math]. This calculation is performed, and we have a temporary result that is correct in the final two digits.

In general, for each position [math]\displaystyle{ n }[/math] in the final result, we sum for all [math]\displaystyle{ i }[/math]:

[math]\displaystyle{ a \text{ (digit at } i\text{ )} \times b \text{ (digit at } (n-i)\text{)}. }[/math]

People can learn this algorithm and thus multiply four-digit numbers in their head – writing down only the final result. They would write it out starting with the rightmost digit and finishing with the leftmost.

Trachtenberg defined this algorithm with a kind of pairwise multiplication where two digits are multiplied by one digit, essentially only keeping the middle digit of the result. By performing the above algorithm with this pairwise multiplication, even fewer temporary results need to be held.

Example: [math]\displaystyle{ 123456 \times 789 }[/math]

To find the first (rightmost) digit of the answer, start at the first digit of the multiplicand

The units digit of [math]\displaystyle{ 9 \times 6 }[/math] is [math]\displaystyle{ 4. }[/math]

The first digit of the answer is [math]\displaystyle{ 4 }[/math]. The tens digit [math]\displaystyle{ 5 }[/math] is ignored.

To find the second digit of the answer, start at the second digit of the multiplicand:

The units digit of [math]\displaystyle{ 9 \times 5 }[/math] plus the tens digit of [math]\displaystyle{ 9 \times 6 }[/math] plus

The units digit of [math]\displaystyle{ 8 \times 6 }[/math].

[math]\displaystyle{ 5 + 5 + 8 = 18 }[/math].

The second digit of the answer is [math]\displaystyle{ 8 }[/math] and carry [math]\displaystyle{ 1 }[/math] to the third digit.

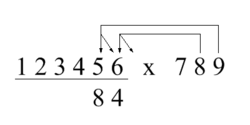
To find the third digit of the answer, start at the third digit of the multiplicand:

The units digit of [math]\displaystyle{ 9 \times 4 }[/math] plus the tens digit of [math]\displaystyle{ 9 \times 5 }[/math] plus

The units digit of [math]\displaystyle{ 8 \times 5 }[/math] plus the tens digit of [math]\displaystyle{ 8 \times 6 }[/math] plus

The units digit of [math]\displaystyle{ 7 \times 6 }[/math]

[math]\displaystyle{ 1 + 6 + 4 + 0 + 4 + 2 = 17 }[/math]

The third digit of the answer is [math]\displaystyle{ 7 }[/math] and carry [math]\displaystyle{ 1 }[/math] to the next digit.

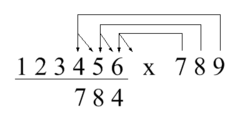
To find the fourth digit of the answer, start at the fourth digit of the multiplicand:

The units digit of [math]\displaystyle{ 9 \times 3 }[/math] plus the tens digit of [math]\displaystyle{ 9 \times 4 }[/math] plus

The units digit of [math]\displaystyle{ 8 \times 4 }[/math] plus the tens digit of [math]\displaystyle{ 8 \times 5 }[/math] plus

The units digit of [math]\displaystyle{ 7 \times 5 }[/math] plus the tens digit of [math]\displaystyle{ 7 \times 6 }[/math].

[math]\displaystyle{ 1 + 7 + 3 + 2 + 4 + 5 + 4 = 26 }[/math] carried from the third digit.

The fourth digit of the answer is [math]\displaystyle{ 6 }[/math] and carry [math]\displaystyle{ 2 }[/math] to the next digit.

Continue with the same method to obtain the remaining digits.

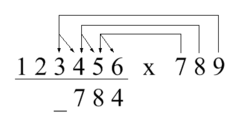
Trachtenberg called this the 2 Finger Method. The calculations for finding the fourth digit from the example above are illustrated at right. The arrow from the nine will always point to the digit of the multiplicand directly above the digit of the answer you wish to find, with the other arrows each pointing one digit to the right. Each arrow head points to a UT Pair, or Product Pair. The vertical arrow points to the product where we will get the Units digit, and the sloping arrow points to the product where we will get the Tens digits of the Product Pair. If an arrow points to a space with no digit there is no calculation for that arrow. As you solve for each digit you will move each of the arrows over the multiplicand one digit to the left until all of the arrows point to prefixed zeros.

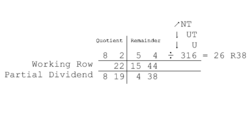
Division in the Trachtenberg System is done much the same as in multiplication but with subtraction instead of addition. Splitting the dividend into smaller Partial Dividends, then dividing this Partial Dividend by only the left-most digit of the divisor will provide the answer one digit at a time. As you solve each digit of the answer you then subtract Product Pairs (UT pairs) and also NT pairs (Number-Tens) from the Partial Dividend to find the next Partial Dividend. The Product Pairs are found between the digits of the answer so far and the divisor. If a subtraction results in a negative number you have to back up one digit and reduce that digit of the answer by one. With enough practice this method can be done in your head.

General addition

A method of adding columns of numbers and accurately checking the result without repeating the first operation. An intermediate sum, in the form of two rows of digits, is produced. The answer is obtained by taking the sum of the intermediate results with an L-shaped algorithm. As a final step, the checking method that is advocated both removes the risk of repeating any original errors and identifies the precise column in which an error occurs all at once. It is based on check (or digit) sums, such as the nines-remainder method.

For the procedure to be effective, the different operations used in each stage must be kept distinct, otherwise there is a risk of interference.

Other multiplication algorithms

When performing any of these multiplication algorithms the following "steps" should be applied.

The answer must be found one digit at a time starting at the least significant digit and moving left. The last calculation is on the leading zero of the multiplicand.

Each digit has a neighbor, i.e., the digit on its right. The rightmost digit's neighbor is the trailing zero.

The 'halve' operation has a particular meaning to the Trachtenberg system. It is intended to mean "half the digit, rounded down" but for speed reasons people following the Trachtenberg system are encouraged to make this halving process instantaneous. So instead of thinking "half of seven is three and a half, so three" it's suggested that one thinks "seven, three". This speeds up calculation considerably. In this same way the tables for subtracting digits from 10 or 9 are to be memorized.

And whenever the rule calls for adding half of the neighbor, always add 5 if the current digit is odd. This makes up for dropping 0.5 in the next digit's calculation.

Numbers and digits (base 10)

Digits and numbers are two different notions. The number T consists of n digits c_n ... c₁.

Multiplying by 2

Proof

Rule:

1. Multiply each digit by 2 (with carrying).

Example: 8624 × 2

Working from left to right:

8+8=16,

6+6=12 (carry the 1),

2+2=4

4+4=8;

8624 × 2 = 17248

Example: 76892 × 2

Working from left to right:

7+7=14

6+6=12

8+8=16

9+9=18

2+2=4;

76892 × 2 =153784

Multiplying by 3

Proof

Rule:

1. Subtract the rightmost digit from 10.
2. Subtract the remaining digits from 9.
3. Double the result.
4. Add half of the neighbor to the right, plus 5 if the digit is odd.
5. For the leading zero, subtract 2 from half of the neighbor.

Example: 492 × 3 = 1476

Working from right to left:

(10 − 2) × 2 + Half of 0 (0) = 16. Write 6, carry 1.

(9 − 9) × 2 + Half of 2 (1) + 5 (since 9 is odd) + 1 (carried) = 7. Write 7.

(9 − 4) × 2 + Half of 9 (4) = 14. Write 4, carry 1.

Half of 4 (2) − 2 + 1 (carried) = 1. Write 1.

Multiplying by 4

Proof

Rule:

1. Subtract the right-most digit from 10.
2. Subtract the remaining digits from 9.
3. Add half of the neighbor, plus 5 if the digit is odd.
4. For the leading 0, subtract 1 from half of the neighbor.

Example: 346 × 4 = 1384

Working from right to left:

(10 − 6) + Half of 0 (0) = 4. Write 4.

(9 − 4) + Half of 6 (3) = 8. Write 8.

(9 − 3) + Half of 4 (2) + 5 (since 3 is odd) = 13. Write 3, carry 1.

Half of 3 (1) − 1 + 1 (carried) = 1. Write 1.

Multiplying by 5

Proof

Rule:

1. Take half of the neighbor, then, if the current digit is odd, add 5.

Example: 42×5=210

Half of 2's neighbor, the trailing zero, is 0.

Half of 4's neighbor is 1.

Half of the leading zero's neighbor is 2.

43×5 = 215

Half of 3's neighbor is 0, plus 5 because 3 is odd, is 5.

Half of 4's neighbor is 1.

Half of the leading zero's neighbor is 2.

93×5=465

Half of 3's neighbor is 0, plus 5 because 3 is odd, is 5.

Half of 9's neighbor is 1, plus 5 because 9 is odd, is 6.

Half of the leading zero's neighbor is 4.

Multiplying by 6

Proof

Rule:

1. Add half of the neighbor to each digit. If the current digit is odd, add 5.

Example: 357 × 6 = 2142

Working right to left:

7 has no neighbor, add 5 (since 7 is odd) = 12. Write 2, carry the 1.

5 + half of 7 (3) + 5 (since the starting digit 5 is odd) + 1 (carried) = 14. Write 4, carry the 1.

3 + half of 5 (2) + 5 (since 3 is odd) + 1 (carried) = 11. Write 1, carry 1.

0 + half of 3 (1) + 1 (carried) = 2. Write 2.

Multiplying by 7

Proof

Rule:

1. Double each digit.
2. Add half of its neighbor to the right (dropping decimals, if any). The neighbor of the units position is 0.
3. If the base-digit is even add 0 otherwise add 5.
4. Add in any carryover from the previous step.

Example: 693 × 7 = 4,851

Working from right to left:

(3×2) + 0 + 5 + 0 = 11 = carryover 1, result 1.

(9×2) + 1 + 5 + 1 = 25 = carryover 2, result 5.

(6×2) + 4 + 0 + 2 = 18 = carryover 1, result 8.

(0×2) + 3 + 0 + 1 = 4 = result 4.

Multiplying by 8

Proof

Rule:

1. Subtract right-most digit from 10.
   1. Subtract the remaining digits from 9.
2. Double the result.
3. Add the neighbor.
4. For the leading zero, subtract 2 from the neighbor.

Example: 456 × 8 = 3648

Working from right to left:

(10 − 6) × 2 + 0 = 8. Write 8.

(9 − 5) × 2 + 6 = 14, Write 4, carry 1.

(9 − 4) × 2 + 5 + 1 (carried) = 16. Write 6, carry 1.

4 − 2 + 1 (carried) = 3. Write 3.

Multiplying by 9

Proof

Rule:

1. Subtract the right-most digit from 10.
   1. Subtract the remaining digits from 9.
2. Add the neighbor to the sum
3. For the leading zero, subtract 1 from the neighbor.

For rules 9, 8, 4, and 3 only the first digit is subtracted from 10. After that each digit is subtracted from nine instead.

Example: 2,130 × 9 = 19,170

Working from right to left:

(10 − 0) + 0 = 10. Write 0, carry 1.

(9 − 3) + 0 + 1 (carried) = 7. Write 7.

(9 − 1) + 3 = 11. Write 1, carry 1.

(9 − 2) + 1 + 1 (carried) = 9. Write 9.

2 − 1 = 1. Write 1.

Multiplying by 10

Add 0 (zero) as the rightmost digit.

Proof

Multiplying by 11

Proof

Rule:

1. Add the digit to its neighbor. (By "neighbor" we mean the digit on the right.)

Example: [math]\displaystyle{ 3,425 \times 11 = 37,675 }[/math]

(0 + 3) (3 + 4) (4 + 2) (2 + 5) (5 + 0)

3 7 6 7 5

To illustrate:

11=10+1

Thus,

[math]\displaystyle{ 3425 \times 11 = 3425 \times (10+1) }[/math]

[math]\displaystyle{ \rightarrow 37675 = 34250 + 3425 }[/math]

Multiplying by 12

Proof

Rule: to multiply by 12:
Starting from the rightmost digit, double each digit and add the neighbor. (The "neighbor" is the digit on the right.)

If the answer is greater than a single digit, simply carry over the extra digit (which will be a 1 or 2) to the next operation. The remaining digit is one digit of the final result.

Example: [math]\displaystyle{ 316 \times 12 }[/math]

Determine neighbors in the multiplicand 0316:

• digit 6 has no right neighbor
• digit 1 has neighbor 6
• digit 3 has neighbor 1
• digit 0 (the prefixed zero) has neighbor 3

[math]\displaystyle{ \begin{align} 6 \times 2 & = 12 \text{ (2 carry 1) } \\ 1 \times 2 + 6 + 1 & = 9 \\ 3 \times 2 + 1 & = 7 \\ 0 \times 2 + 3 & = 3 \\ 0 \times 2 + 0 & = 0 \\[10pt] 316 \times 12 & = 3,792 \end{align} }[/math]

Multiplying by 13

Proof

Publications

• Rushan Ziatdinov, Sajid Musa. Rapid mental computation system as a tool for algorithmic thinking of elementary school students development. European Researcher 25(7): 1105–1110, 2012 [1].
• The Trachtenberg Speed System of Basic Mathematics by Jakow Trachtenberg, A. Cutler (Translator), R. McShane (Translator), was published by Doubleday and Company, Inc. Garden City, New York in 1960.^[1]

The book contains specific algebraic explanations for each of the above operations.

Most of the information in this article is from the original book.

The algorithms/operations for multiplication, etc., can be expressed in other more compact ways that the book does not specify, despite the chapter on algebraic description.^{[lower-alpha 1]}

In popular culture

The 2017 American film Gifted revolves around a child prodigy who at the age of 7 impresses her teacher by doing calculations in her head using the Trachtenberg system.^[2]

Other systems

There are many other methods of calculation in mental mathematics. The list below shows a few other methods of calculating, though they may not be entirely mental.

• Bharati Krishna Tirtha's book "Vedic Mathematics"
• Mental abacus – As students become used to manipulating the abacus with their fingers, they are typically asked to do calculation by visualizing abacus in their head. Almost all proficient abacus users are adept at doing arithmetic mentally.^{[citation needed]}
• Chisanbop

Notes

References

Further reading

• Trachtenberg, J. (1960). The Trachtenberg Speed System of Basic Mathematics. Doubleday and Company, Inc., Garden City, NY, USA.
• Катлер Э., Мак-Шейн Р.Система быстрого счёта по Трахтенбергу, 1967 (in Russian).
• Rushan Ziatdinov, Sajid Musa. "Rapid Mental Computation System as a Tool for Algorithmic Thinking of Elementary School Students Development", European Researcher 25(7): 1105–1110, 2012.

External links

• Chandrashekhar, Kiran.
• Gifted (2017 film), This film is more about the Trachtenberg system, with Mckenna Grace, a young artist who has learned this technique, playing the lead role.
• Vedic Mathematics Academy

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Trachtenberg system. Read more