Tree (automata theory)

In automata theory, a tree is a particular way of representing a tree structure as sequences of natural numbers.

Graphic illustration of the labeled tree described in the example

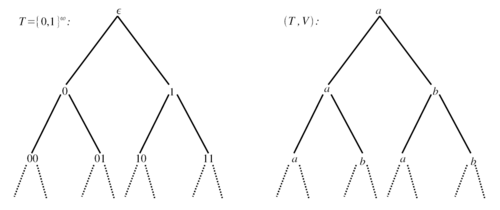
For example, each node of the tree is a word over set of natural numbers ([math]\displaystyle{ \mathbb{N} }[/math]), which helps this definition to be used in automata theory.

A tree is a set T ⊆ [math]\displaystyle{ \mathbb{N} }[/math]^* such that if t.c ∈ T, with t ∈ [math]\displaystyle{ \mathbb{N} }[/math]^* and c ∈ [math]\displaystyle{ \mathbb{N} }[/math], then t ∈ T and t.c₁ ∈ T for all 0 ≤ c₁ < c. The elements of T are known as nodes, and the empty word ε is the (single) root of T. For every t ∈ T, the element t.c ∈ T is a successor of t in direction c. The number of successors of t is called its degree or arity, and represented as d(t). A node is a leaf if it has no successors. If every node of a tree has finitely many successors, then it is called a finitely, otherwise an infinitely branching tree. A path π is a subset of T such that ε ∈ π and for every t ∈ T, either t is a leaf or there exists a unique c ∈ [math]\displaystyle{ \mathbb{N} }[/math] such that t.c ∈ π. A path may be a finite or infinite set. If all paths of a tree are finite then the tree is called finite, otherwise infinite. A tree is called fully infinite if all its paths are infinite. Given an alphabet Σ, a Σ-labeled tree is a pair (T,V), where T is a tree and V: T → Σ maps each node of T to a symbol in Σ. A labeled tree formally defines a commonly used term tree structure. A set of labeled trees is called a tree language.

A tree is called ordered if there is an order among the successors of each of its nodes. The above definition of tree naturally suggests an order among the successors, which can be used to make the tree ranked.

In the case of ranked alphabets, an extra function Ar: Σ → [math]\displaystyle{ \mathbb{N} }[/math] is defined. This function associates a fixed arity to each symbol of the alphabet. In this case, each t ∈ T has to satisfy Ar(V(t)) = d(t). The trees that satisfy this property are called ranked trees. The trees that do not (necessarily) satisfy that property are called unranked.

For example, the above definition is used in the definition of an infinite tree automaton.

Example

Let T = {0,1}^* and Σ = {a,b}. We define a labeling function V as follows: the labeling for the root node is V(ε) = a and, for every other node t ∈ {0,1}^*, the labellings for its successor nodes are V(t.0) = a and V(t.1) = b. It is clear from the picture that T forms a (fully) infinite binary tree.

References

• Comon, Hubert; Dauchet, Max; Gilleron, Rémi; Jacquemard, Florent; Lugiez, Denis; Löding, Christof; Tison, Sophie; Tommasi, Marc (November 2008). "Preliminaries". Tree Automata Techniques and Applications. https://gforge.inria.fr/frs/download.php/10994/tata.pdf. Retrieved 11 February 2014. 

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Tree (automata theory). Read more