Table of Contents Categories
  Encyclosphere.org ENCYCLOREADER
  supported by EncyclosphereKSF

Turn (angle)

From HandWiki - Reading time: 10 min
Short description: Unit of angle equal to 2𝜋 radians

Turn
Unit ofPlane angle
Symboltr or pla 
Conversions
1 tr in ...... is equal to ...
   radians   2π rad
≈ 6.283185307... rad
   milliradians   2000π mrad
≈ 6283.185307... mrad
   degrees   360°
   gradians   400g
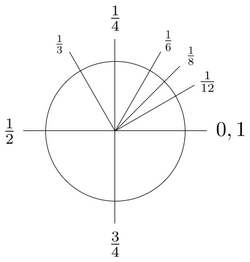
Counterclockwise rotations about the center point where a complete rotation corresponds to an angle of rotation of 1 turn.

A turn is a unit of plane angle measurement equal to 2π radians, 360 degrees or 400 gradians. Subdivisions of a turn include half-turns, quarter-turns, centiturns, milliturns, etc.

One turn corresponds[1] to one cycle[2] or to one revolution,[3] although those terms may also be used, ambiguously, as shorter version of the units of frequency cycles per second (cps) and revolutions per minute (rpm), respectively.

Subdivisions

A turn can be divided in 100 centiturns or 1000 milliturns, with each milliturn corresponding to an angle of 0.36°, which can also be written as 21′ 36″.[4][5] A protractor divided in centiturns is normally called a "percentage protractor".

Binary fractions of a turn are also used. Sailors have traditionally divided a turn into 32 compass points, which implicitly have an angular separation of 1/32 turn. The binary degree, also known as the binary radian (or brad), is 1/256 turn.[6] The binary degree is used in computing so that an angle can be represented to the maximum possible precision in a single byte. Other measures of angle used in computing may be based on dividing one whole turn into 2n equal parts for other values of n.[7]

The notion of turn is commonly used for planar rotations.

History

The word turn originates via Latin and French from the Greek word τόρνος (tórnos – a lathe).

In 1697, David Gregory used π/ρ (pi over rho) to denote the perimeter of a circle (i.e., the circumference) divided by its radius.[8][9] However, earlier in 1647, William Oughtred had used δ/π (delta over pi) for the ratio of the diameter to perimeter. The first use of the symbol π on its own with its present meaning (of perimeter divided by diameter) was in 1706 by the Welsh mathematician William Jones.[10] Euler adopted the symbol with that meaning in 1737, leading to its widespread use.

The Latin word for turn is versor, which represents a rotation about an arbitrary axis in three-dimensional space. Versors form points in elliptic space and motivate the study of quaternions, an algebra developed by W. R. Hamilton in the 1840s.

Percentage protractors have existed since 1922,[11] but the terms centiturns, milliturns and microturns were introduced much later by the British astronomer Fred Hoyle in 1962.[4][5] Some measurement devices for artillery and satellite watching carry milliturn scales.[12][13]

Unit symbols

The German standard DIN 1315 (March 1974) proposed the unit symbol "pla" (from Latin: plenus angulus 'full angle') for turns.[14][15] Covered in DIN 1301-1 (de) (October 2010), the so-called Vollwinkel ('full angle') is not an SI unit. However, it is a legal unit of measurement in the EU[16][17] and Switzerland.[18]

The scientific calculators HP 39gII and HP Prime support the unit symbol "tr" for turns since 2011 and 2013, respectively. Support for "tr" was also added to newRPL for the HP 50g in 2016, and for the hp 39g+, HP 49g+, HP 39gs, and HP 40gs in 2017.[19][20] An angular mode TURN was suggested for the WP 43S as well,[21] but the calculator instead implements "MULπ" (multiples of π) as mode and unit since 2019.[22][23]

Unit conversion

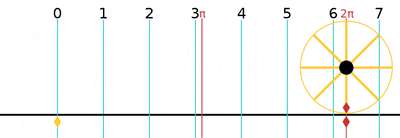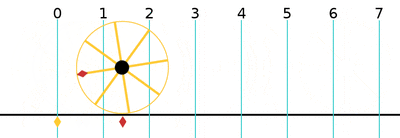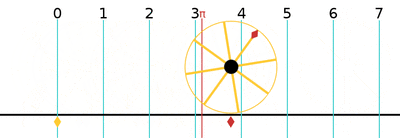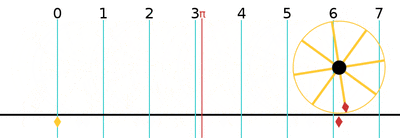
The circumference of the unit circle (whose radius is one) is 2π.
A comparison of angles expressed in degrees and radians.

One turn is equal to 2π (≈ 6.283185307179586)[24] radians, 360 degrees, or 400 gradians.

Conversion of common angles
Turns Radians Degrees Gradians
0 turn 0 rad 0° 0g
1/72 turn Template:Tau/72 rad[lower-alpha 1] π/36 rad 5° 5+5/9g
1/24 turn Template:Tau/24 rad π/12 rad 15° 16+2/3g
1/16 turn Template:Tau/16 rad π/8 rad 22.5° 25g
1/12 turn Template:Tau/12 rad π/6 rad 30° 33+1/3g
1/10 turn Template:Tau/10 rad π/5 rad 36° 40g
1/8 turn Template:Tau/8 rad π/4 rad 45° 50g
1/2π turn 1 rad c. 57.3° c. 63.7g
1/6 turn Template:Tau/6 rad π/3 rad 60° 66+2/3g
1/5 turn Template:Tau/5 rad 2π/5 rad 72° 80g
1/4 turn Template:Tau/4 rad π/2 rad 90° 100g
1/3 turn Template:Tau/3 rad 2π/3 rad 120° 133+1/3g
2/5 turn 2Template:Tau/5 rad 4π/5 rad 144° 160g
1/2 turn Template:Tau/2 rad π rad 180° 200g
3/4 turn 3Template:Tau/4 rad 3π/2 rad 270° 300g
1 turn Template:Tau rad 2π rad 360° 400g
  1. ↑ In this table, 𝜏 denotes 2π.

Proposals for a single letter to represent 2π

An arc of a circle with the same length as the radius of that circle corresponds to an angle of 1 radian. A full circle corresponds to a full turn, or approximately 6.28 radians, which is expressed here using the Greek letter tau (τ).

In 1746, Leonhard Euler first used the Greek letter pi to represent the circumference divided by the radius of a circle (i.e., π = 6.28...).[25]

In 2001, Robert Palais proposed using the number of radians in a turn as the fundamental circle constant instead of π, which amounts to the number of radians in half a turn, in order to make mathematics simpler and more intuitive. His proposal used a "π with three legs" symbol to denote the constant ([math]\displaystyle{ \pi\!\;\!\!\!\pi = 2\pi }[/math]).[26]

In 2008, Thomas Colignatus proposed the uppercase Greek letter theta, Θ, to represent 2π.[27] The Greek letter theta derives from the Phoenician and Hebrew letter teth, 𐤈 or ט, and it has been observed that the older version of the symbol, which means wheel, resembles a wheel with four spokes.[28] It has also been proposed to use the wheel symbol, teth, to represent the quantity 2π, and more recently a connection has been made among other ancient cultures on the existence of a wheel, sun, circle, or disk symbol—i.e. other variations of teth—as representation for 2π.[29]

In 2010, Michael Hartl proposed to use the Greek letter tau to represent the circle constant: τ = 2π. He offered two reasons. First, τ is the number of radians in one turn, which allows fractions of a turn to be expressed more directly: for instance, a 3/4 turn would be represented as 3τ/4 rad instead of 3π/2 rad. Second, τ visually resembles π, whose association with the circle constant is unavoidable.[30] Hartl's Tau Manifesto[31] gives many examples of formulas that are asserted to be clearer where τ is used instead of π,[32][33][34] such as a tighter association with the geometry of Euler's identity using eiτ = 1 instead of eiπ = −1.

Initially, neither of these proposals received widespread acceptance by the mathematical and scientific communities.[35] However, the use of τ has become more widespread,[36] for example:

The following table shows how various identities appear if τ = 2π was used instead of π.[50][26] For a more complete list, see List of formulae involving π.

Formula Using π Using τ Notes
Angle subtended by 1/4 of a circle π/2 rad τ/4 rad τ/4 rad = 1/4 turn
Circumference C of a circle of radius r C = 2πr C = τr
Area of a circle A = πr2 A = 1/2τr2 The area of a sector of angle θ is A = 1/2θr2.
Area of a regular n-gon with unit circumradius A = n/2 sin 2π/n A = n/2 sin τ/n
n-ball and n-sphere volume recurrence relation Vn(r) = r/n Sn−1(r) Sn(r) = 2πr Vn−1(r) Vn(r) = r/n Sn−1(r) Sn(r) = τr Vn−1(r) V0(r) = 1
S0(r) = 2
Cauchy's integral formula [math]\displaystyle{ f(a) = \frac{1}{2\pi i} \oint_\gamma \frac{f(z)}{z-a}\, dz }[/math] [math]\displaystyle{ f(a) = \frac{1}{\tau i} \oint_\gamma \frac{f(z)}{z-a}\, dz }[/math]
Standard normal distribution [math]\displaystyle{ \varphi(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} }[/math] [math]\displaystyle{ \varphi(x) = \frac{1}{\sqrt{\tau}}e^{-\frac{x^2}{2}} }[/math]
Stirling's approximation [math]\displaystyle{ n! \sim \sqrt{2 \pi n}\left(\frac{n}{e}\right)^n }[/math] [math]\displaystyle{ n! \sim \sqrt{\tau n}\left(\frac{n}{e}\right)^n }[/math]
Euler's identity 0       eiπ = −1
eiπ + 1 = 0 		0     eiτ = 1
eiτ - 1 = 0 		For any integer k, eikτ = 1
nth roots of unity [math]\displaystyle{ e^{2 \pi i \frac{k}{n}} = \cos\frac{2 k \pi}{n} + i \sin\frac{2 k \pi}{n} }[/math] [math]\displaystyle{ e^{\tau i \frac{k}{n}} = \cos\frac{k \tau}{n} + i \sin\frac{k \tau}{n} }[/math]
Planck constant [math]\displaystyle{ h = 2 \pi \hbar }[/math] [math]\displaystyle{ h = \tau \hbar }[/math] ħ is the reduced Planck constant.
Angular frequency [math]\displaystyle{ \omega = 2 \pi f }[/math] [math]\displaystyle{ \omega = \tau f }[/math]

Examples of use

  • As an angular unit, the turn is particularly useful in many applications, such as in connection with electromagnetic coils and rotating objects. See also Winding number.
  • Pie charts illustrate proportions of a whole as fractions of a turn. Each one percent is shown as an angle of one centiturn.[11]

See also

References

  1. ↑ Correspondence is not equivalent equality. The cycle and the revolution are not units of angle; also, this correspondence does not hold generally for cyclic phenomena.
  2. ↑ Fitzpatrick, R. (2021). Newtonian Dynamics: An Introduction. CRC Press. p. 116. ISBN 978-1-000-50953-3. https://books.google.com/books?id=rRpSEAAAQBAJ&pg=PA116. Retrieved 2023-04-25. 
  3. ↑ Units & Symbols for Electrical & Electronic Engineers
  4. ↑ 4.0 4.1 Chandler, M. H., ed (1962). Astronomy (1 ed.). London, UK: Macdonald. OCLC 7419446. https://archive.org/details/astronom00hoyl.  (320 pages)
  5. ↑ 5.0 5.1 "Chapter 8: Keeping Track of Time". The Science of Measurement: A Historical Survey (The World of Measurements: Masterpieces, Mysteries and Muddles of Metrology). Dover Books on Mathematics (corrected reprint of original ed.). Dover Publications, Inc. / Courier Corporation (originally by Simon & Schuster, Inc.). 2012. p. 102. ISBN 978-0-48614497-9. https://books.google.com/books?id=CrmuSiCFyikC&pg=PA102. Retrieved 2019-08-06.  (736 pages)
  6. ↑ "ooPIC Programmer's Guide - Chapter 15: URCP". ooPIC Manual & Technical Specifications - ooPIC Compiler Ver 6.0. Savage Innovations, LLC. 2007. http://www.oopic.com/pgchap15.htm. 
  7. ↑ "Angles, integers, and modulo arithmetic". blogs.msdn.com. http://blogs.msdn.com/shawnhar/archive/2010/01/04/angles-integers-and-modulo-arithmetic.aspx. 
  8. ↑ A History of Pi. Barnes & Noble Publishing. 1989. 
  9. ↑ The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. The Mathematical Association of America. 1994. p. 165. ISBN 978-0-88385511-9. https://archive.org/details/wordsofmathemati0000schw. 
  10. ↑ "Pi through the ages". 2001. http://www.veling.nl/anne/templars/Pi_through_the_ages.html. 
  11. ↑ 11.0 11.1 "A Percentage Protractor - Designed for Use in the Construction of Circle Charts or "Pie Diagrams"". Journal of the American Statistical Association. Short Note 18 (137): 108–109. 1922. doi:10.1080/01621459.1922.10502455. 
  12. ↑ "Bestimmung von Satellitenbahnen" (in de). Mitteilungen der Uraniasternwarte (Wien). 1965. 
  13. ↑ Trackers of the Skies. History of the Smithsonian Satellite-tracking Program. Cambridge, Massachusetts, USA: Academic Press / Howard A. Doyle Publishing Company. 1975. https://siris-sihistory.si.edu/ipac20/ipac.jsp?&profile=all&source=~!sichronology&uri=full=3100001~!3190~!0#focus. 
  14. ↑ (in de) Handbuch SI-Einheiten: Definition, Realisierung, Bewahrung und Weitergabe der SI-Einheiten, Grundlagen der Präzisionsmeßtechnik (1 ed.). Friedrich Vieweg & Sohn Verlagsgesellschaft mbH, reprint: Springer-Verlag. 2013-03-13. p. 421. 978-3-528-08441-7, 978-3-32283606-9. ISBN 978-3-32283606-9. https://books.google.com/books?id=63qcBgAAQBAJ&pg=PA421. Retrieved 2015-08-14. 
  15. ↑ (in de) Das Vieweg Einheiten-Lexikon: Formeln und Begriffe aus Physik, Chemie und Technik (1 ed.). Vieweg, reprint: Springer-Verlag. 2013-03-09. p. 403. doi:10.1007/978-3-322-92920-4. 978-3-322-92921-1. ISBN 978-3-32292920-4. https://books.google.com/books?id=2zecBgAAQBAJ. Retrieved 2015-08-14. 
  16. ↑ "Richtlinie 80/181/EWG - Richtlinie des Rates vom 20. Dezember 1979 zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Meßwesen und zur Aufhebung der Richtlinie 71/354/EWG" (in de). 1980-02-15. https://eur-lex.europa.eu/legal-content/DE/TXT/PDF/?uri=CELEX:01980L0181-20090527. 
  17. ↑ "Richtlinie 2009/3/EG des Europäischen Parlaments und des Rates vom 11. März 2009 zur Änderung der Richtlinie 80/181/EWG des Rates zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Messwesen (Text von Bedeutung für den EWR)" (in de). 2009-03-11. https://eur-lex.europa.eu/legal-content/DE/TXT/PDF/?uri=CELEX:32009L0003&from=EN. 
  18. ↑ "Art. 15 Einheiten in Form von nichtdezimalen Vielfachen oder Teilen von SI-Einheiten" (in de-ch). Einheitenverordnung. Schweizerischer Bundesrat. 1994-11-23. 941.202. http://www.admin.ch/opc/de/classified-compilation/19940345/. Retrieved 2013-01-01. 
  19. ↑ "RE: newRPL: Handling of units". HP Museum. 2016-05-11. http://www.hpmuseum.org/forum/thread-4783-post-55836.html#pid55836. 
  20. ↑ "Chapter 3: Units - Available Units - Angles". newRPL User Manual. 2018-10-25. https://newrpl.wiki.hpgcc3.org/doku.php?id=manual:chapter3:units#available-units. Retrieved 2019-08-07. 
  21. ↑ "RE: WP-32S in 2016?". HP Museum. 2016-01-12. https://www.hpmuseum.org/forum/thread-5427-post-48945.html#pid48945. "[...] I'd like to see a TURN mode being implemented as well. TURN mode works exactly like DEG, RAD and GRAD (including having a full set of angle unit conversion functions like on the WP 34S), except for that a full circle doesn't equal 360 degree, 6.2831... rad or 400 gon, but 1 turn. (I […] found it to be really convenient in engineering/programming, where you often have to convert to/from other unit representations […] But I think it can also be useful for educational purposes. [...] Having the angle of a full circle normalized to 1 allows for easier conversions to/from a whole bunch of other angle units […]" 
  22. ↑ WP 43S Owner's Manual (draft ed.). 2019. pp. 72, 118–119, 311. ISBN 978-1-72950098-9. https://gitlab.com/wpcalculators/wp43/-/raw/master/docs/OwnersManual.pdf. Retrieved 2019-08-05.  [1] [2] (314 pages)
  23. ↑ WP 43S Reference Manual (draft ed.). 2019. pp. iii, 54, 97, 128, 144, 193, 195. ISBN 978-1-72950106-1. https://gitlab.com/wpcalculators/wp43/-/raw/master/docs/ReferenceManual.pdf. Retrieved 2019-08-05.  [3] [4] (271 pages)
  24. ↑ Sequence OEIS: A019692
  25. ↑ Euler, L. (1746). Nova theoria lucis et colorum. Opuscula varii argumenti, p. 169–244.
  26. ↑ 26.0 26.1 "Pi is Wrong". The Mathematical Intelligencer (New York, USA: Springer-Verlag) 23 (3): 7–8. 2001. doi:10.1007/bf03026846. http://www.math.utah.edu/%7Epalais/pi.pdf. Retrieved 2019-08-05. 
  27. ↑ Colignatus, Th., "Trig rerigged. Trigonometry reconsidered. Measuring angles in 'unit meter around' and using the unit radius functions Xur and Yur". 2008-04-08, Legacy:COTP.
  28. ↑ Mann, S., Janzen, R., Ali, M. A., Scourboutakos, P., & Guleria, N. (October 2014). Integral kinematics (time-integrals of distance, energy, etc.) and integral kinesiology. In Proceedings of the 2014 IEEE GEM, Toronto, ON, Canada (pp. 22–24)
  29. ↑ Mann, S., Defaz, D., Pierce, C., Lam, D., Stairs, J., Hermandez, J., ... & Mann, C. (June 2019). Keynote-Eye Itself as a Camera: Sensors, Integrity, and Trust. In The 5th ACM Workshop on Wearable Systems and Applications (pp. 1–2).
  30. ↑ "The Tau Manifesto". 2019-03-14. http://tauday.com/tau-manifesto. 
  31. ↑ "The Tau Manifesto". 2010-03-14. https://hexnet.org/files/documents/tau-manifesto.pdf. 
  32. ↑ "Michael Hartl: It's time to kill off pi". New Scientist. Interview 209 (2794): 23. 2011-01-08. doi:10.1016/S0262-4079(11)60036-5. Bibcode: 2011NewSc.209...23A. 
  33. ↑ "On Pi Day, is 'pi' under attack?". cnn.com. CNN. 2011-03-14. http://edition.cnn.com/2011/TECH/innovation/03/14/pi.tau.math/index.html. 
  34. ↑ "Let's Use Tau--It's Easier Than Pi - A growing movement argues that killing pi would make mathematics simpler, easier and even more beautiful". Scientific American. 2014-06-25. http://www.scientificamerican.com/article/let-s-use-tau-it-s-easier-than-pi/. 
  35. ↑ "Life of pi in no danger – Experts cold-shoulder campaign to replace with tau". Telegraph India. 2011-06-30. http://www.telegraphindia.com/1110630/jsp/nation/story_14178997.jsp. Retrieved 2019-08-05. 
  36. ↑ "For Math Fans, Nothing Can Spoil Pi Day—Except Maybe Tau Day" (in en-US). Wall Street Journal. 2020-03-13. ISSN 0099-9660. https://www.wsj.com/articles/for-math-fans-nothing-can-spoil-pi-dayexcept-maybe-tau-day-11584123031. 
  37. ↑ "Happy Tau Day!" (in en-US). 28 June 2012. https://blog.khanacademy.org/happy-tau-day/. 
  38. ↑ "Supported Functions". https://help.desmos.com/hc/en-us/articles/212235786-Supported-Functions. 
  39. ↑ "PEP 628 -- Add math.tau". Python.org. 2017-02-25. https://www.python.org/dev/peps/pep-0628/. 
  40. ↑ "math — Mathematical functions". Python 3.7.0 documentation. https://docs.python.org/3/library/math.html#math.tau. 
  41. ↑ "Perl 6 terms". https://docs.perl6.org/language/terms. 
  42. ↑ "TAU". Processing. https://processing.org/reference/TAU.html. 
  43. ↑ "math". Nim. https://nim-lang.org/docs/math.html. 
  44. ↑ "std::f64::consts::TAU - Rust". https://doc.rust-lang.org/stable/std/f64/consts/constant.TAU.html. 
  45. ↑ "JDK-8283136: Add constant for tau to Math and StrictMath". https://bugs.openjdk.org/browse/JDK-8283136. 
  46. ↑ John-H-K. "Add Math.Tau Pull Request #37517 · dotnet/Runtime". https://github.com/dotnet/runtime/pull/37517. 
  47. ↑ "tau: Tau, the ratio between any circle's circumference and radius.". https://hackage.haskell.org/package/tau. 
  48. ↑ "Bounds on tail probabilities for negative binomial distributions". Kybernetika 52 (6): 943–966. 2017. doi:10.14736/kyb-2016-6-0943. 
  49. ↑ "Al-Kashi's constant τ". 2018-11-17. http://www.harremoes.dk/Peter/Undervis/Turnpage/Turnpage1.pdf. 
  50. ↑ "My Conversion to Tauism". Math Horizons 19 (4): 34. April 2012. doi:10.4169/mathhorizons.19.4.34. http://www.maa.org/sites/default/files/pdf/Mathhorizons/apr12_aftermath.pdf. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Turn_(angle)&oldid=3010473"
Licensed under CC BY-SA 3.0 | Source: https://handwiki.org/wiki/Turn_(angle)
7 views | Status: cached on September 14 2024 08:40:15
↧ Download this article as ZWI file
Encyclosphere.org EncycloReader is supported by the EncyclosphereKSF