Unification (computer science)

In logic and computer science, unification is an algorithmic process of solving equations between symbolic expressions. For example, using x,y,z as variables, the singleton equation set { cons(x,cons(x,nil)) = cons(2,y) } is a syntactic first-order unification problem that has the substitution { x ↦ 2, y ↦ cons(2,nil) } as its only solution. A unification algorithm was first discovered by Jacques Herbrand,^[1][2][3] while a first formal investigation can be attributed to John Alan Robinson,^[4][5] who used first-order syntactical unification as a basic building block of his resolution procedure for first-order logic, a great step forward in automated reasoning technology, as it eliminated one source of combinatorial explosion: searching for instantiation of terms. Today, automated reasoning is still the main application area of unification. Syntactical first-order unification is used in logic programming and programming language type system implementation, especially in Hindley–Milner based type inference algorithms. Semantic unification is used in SMT solvers, term rewriting algorithms and cryptographic protocol analysis. Higher-order unification is used in proof assistants, for example Isabelle and Twelf, and restricted forms of higher-order unification (higher-order pattern unification) are used in some programming language implementations, such as lambdaProlog, as higher-order patterns are expressive, yet their associated unification procedure retains theoretical properties closer to first-order unification.

Formal definition

A unification problem is a finite set E={ l₁ ≐ r₁, ..., l_n ≐ r_n } of equations to solve, where l_i, r_i are in the set [math]\displaystyle{ T }[/math] of terms or expressions. Depending on which expressions or terms are allowed to occur in an equation set or unification problem, and which expressions are considered equal, several frameworks of unification are distinguished. If higher-order variables, that is, variables representing functions, are allowed in an expression, the process is called higher-order unification, otherwise first-order unification. If a solution is required to make both sides of each equation literally equal, the process is called syntactic or free unification, otherwise semantic or equational unification, or E-unification, or unification modulo theory.

If the right side of each equation is closed (no free variables), the problem is called (pattern) matching. The left side (with variables) of each equation is called the pattern.^[6]

Prerequisites

Formally, a unification approach presupposes

• An infinite set [math]\displaystyle{ V }[/math] of variables. For higher-order unification, it is convenient to choose [math]\displaystyle{ V }[/math] disjoint from the set of lambda-term bound variables.
• A set [math]\displaystyle{ T }[/math] of terms such that [math]\displaystyle{ V \subseteq T }[/math]. For first-order unification, [math]\displaystyle{ T }[/math] is usually the set of first-order terms (terms built from variable and function symbols). For higher-order unification [math]\displaystyle{ T }[/math] consists of first-order terms and lambda terms (terms containing some higher-order variables).
• A mapping vars: [math]\displaystyle{ T \rightarrow }[/math] [math]\displaystyle{ \mathbb{P} }[/math][math]\displaystyle{ (V) }[/math], assigning to each term [math]\displaystyle{ t }[/math] the set [math]\displaystyle{ \text{vars}(t) \subsetneq V }[/math] of free variables occurring in [math]\displaystyle{ t }[/math].
• A theory or equivalence relation [math]\displaystyle{ \equiv }[/math] on [math]\displaystyle{ T }[/math], indicating which terms are considered equal. For first-order E-unification, [math]\displaystyle{ \equiv }[/math] reflects the background knowledge about certain function symbols; for example, if [math]\displaystyle{ \oplus }[/math] is considered commutative, [math]\displaystyle{ t\equiv u }[/math] if [math]\displaystyle{ u }[/math] results from [math]\displaystyle{ t }[/math] by swapping the arguments of [math]\displaystyle{ \oplus }[/math] at some (possibly all) occurrences. ^{[note 1]} In the most typical case that there is no background knowledge at all, then only literally, or syntactically, identical terms are considered equal. In this case, ≡ is called the free theory (because it is a free object), the empty theory (because the set of equational sentences, or the background knowledge, is empty), the theory of uninterpreted functions (because unification is done on uninterpreted terms), or the theory of constructors (because all function symbols just build up data terms, rather than operating on them). For higher-order unification, usually [math]\displaystyle{ t\equiv u }[/math] if [math]\displaystyle{ t }[/math] and [math]\displaystyle{ u }[/math] are alpha equivalent.

As an example of how the set of terms and theory affects the set of solutions, the syntactic first-order unification problem { y = cons(2,y) } has no solution over the set of finite terms. However, it has the single solution { y ↦ cons(2,cons(2,cons(2,...))) } over the set of infinite tree terms. Similarly, the semantic first-order unification problem { a⋅x = x⋅a } has each substitution of the form { x ↦ a⋅...⋅a } as a solution in a semigroup, i.e. if (⋅) is considered associative. But the same problem, viewed in an abelian group, where (⋅) is considered also commutative, has any substitution at all as a solution.

As an example of higher-order unification, the singleton set { a = y(x) } is a syntactic second-order unification problem, since y is a function variable. One solution is { x ↦ a, y ↦ (identity function) }; another one is { y ↦ (constant function mapping each value to a), x ↦ (any value) }.

Substitution

Main page: Philosophy:Substitution (logic)

A substitution is a mapping [math]\displaystyle{ \sigma: V\rightarrow T }[/math] from variables to terms; the notation [math]\displaystyle{ \{x_1\mapsto t_1, ..., x_k \mapsto t_k\} }[/math] refers to a substitution mapping each variable [math]\displaystyle{ x_i }[/math] to the term [math]\displaystyle{ t_i }[/math], for [math]\displaystyle{ i=1,...,k }[/math], and every other variable to itself; the [math]\displaystyle{ x_i }[/math] must be pairwise distinct. Applying that substitution to a term [math]\displaystyle{ t }[/math] is written in postfix notation as [math]\displaystyle{ t \{x_1 \mapsto t_1, ..., x_k \mapsto t_k\} }[/math]; it means to (simultaneously) replace every occurrence of each variable [math]\displaystyle{ x_i }[/math] in the term [math]\displaystyle{ t }[/math] by [math]\displaystyle{ t_i }[/math]. The result [math]\displaystyle{ t\tau }[/math] of applying a substitution [math]\displaystyle{ \tau }[/math] to a term [math]\displaystyle{ t }[/math] is called an instance of that term [math]\displaystyle{ t }[/math]. As a first-order example, applying the substitution { x ↦ h(a,y), z ↦ b } to the term

Generalization, specialization

If a term [math]\displaystyle{ t }[/math] has an instance equivalent to a term [math]\displaystyle{ u }[/math], that is, if [math]\displaystyle{ t\sigma \equiv u }[/math] for some substitution [math]\displaystyle{ \sigma }[/math], then [math]\displaystyle{ t }[/math] is called more general than [math]\displaystyle{ u }[/math], and [math]\displaystyle{ u }[/math] is called more special than, or subsumed by, [math]\displaystyle{ t }[/math]. For example, [math]\displaystyle{ x\oplus a }[/math] is more general than [math]\displaystyle{ a\oplus b }[/math] if ⊕ is commutative, since then [math]\displaystyle{ (x\oplus a) \{x\mapsto b\} = b\oplus a\equiv a\oplus b }[/math].

If ≡ is literal (syntactic) identity of terms, a term may be both more general and more special than another one only if both terms differ just in their variable names, not in their syntactic structure; such terms are called variants, or renamings of each other. For example, [math]\displaystyle{ f(x_1, a, g(z_1), y_1) }[/math] is a variant of [math]\displaystyle{ f(x_2, a, g(z_2), y_2) }[/math], since [math]\displaystyle{ f(x_1, a, g(z_1), y_1) \{x_1 \mapsto x_2, y_1 \mapsto y_2, z_1 \mapsto z_2\} = f(x_2, a, g(z_2), y_2) }[/math] and [math]\displaystyle{ f(x_2, a, g(z_2), y_2) \{x_2 \mapsto x_1, y_2 \mapsto y_1, z_2 \mapsto z_1\} = f(x_1, a, g(z_1), y_1). }[/math] However, [math]\displaystyle{ f(x_1, a, g(z_1), y_1) }[/math] is not a variant of [math]\displaystyle{ f(x_2, a, g(x_2), x_2) }[/math], since no substitution can transform the latter term into the former one. The latter term is therefore properly more special than the former one.

For arbitrary [math]\displaystyle{ \equiv }[/math], a term may be both more general and more special than a structurally different term. For example, if ⊕ is idempotent, that is, if always [math]\displaystyle{ x \oplus x \equiv x }[/math], then the term [math]\displaystyle{ x\oplus y }[/math] is more general than [math]\displaystyle{ z }[/math],^{[note 2]} and vice versa,^{[note 3]} although [math]\displaystyle{ x\oplus y }[/math] and [math]\displaystyle{ z }[/math] are of different structure.

A substitution [math]\displaystyle{ \sigma }[/math] is more special than, or subsumed by, a substitution [math]\displaystyle{ \tau }[/math] if [math]\displaystyle{ t\sigma }[/math] is subsumed by [math]\displaystyle{ t\tau }[/math] for each term [math]\displaystyle{ t }[/math]. We also say that [math]\displaystyle{ \tau }[/math] is more general than [math]\displaystyle{ \sigma }[/math]. More formally, take a nonempty infinite set [math]\displaystyle{ V }[/math] of auxiliary variables such that no equation [math]\displaystyle{ l_i \doteq r_i }[/math] in the unification problem contains variables from [math]\displaystyle{ V }[/math]. Then a substitution [math]\displaystyle{ \sigma }[/math] is subsumed by another substitution [math]\displaystyle{ \tau }[/math] if there is a substitution [math]\displaystyle{ \theta }[/math] such that for all terms [math]\displaystyle{ X\notin V }[/math], [math]\displaystyle{ X\sigma \equiv X\tau\theta }[/math].^[7] For instance [math]\displaystyle{ \{x \mapsto a, y \mapsto a \} }[/math] is subsumed by [math]\displaystyle{ \tau = \{x\mapsto y\} }[/math], using [math]\displaystyle{ \theta=\{y\mapsto a\} }[/math], but [math]\displaystyle{ \sigma = \{x\mapsto a\} }[/math] is not subsumed by [math]\displaystyle{ \tau = \{x\mapsto y\} }[/math], as [math]\displaystyle{ f(x, y)\sigma = f(a, y) }[/math] is not an instance of [math]\displaystyle{ f(x, y) \tau = f(y, y) }[/math].^[8]

Solution set

A substitution σ is a solution of the unification problem E if l_iσ ≡ r_iσ for [math]\displaystyle{ i = 1, ..., n }[/math]. Such a substitution is also called a unifier of E. For example, if ⊕ is associative, the unification problem { x ⊕ a ≐ a ⊕ x } has the solutions {x ↦ a}, {x ↦ a ⊕ a}, {x ↦ a ⊕ a ⊕ a}, etc., while the problem { x ⊕ a ≐ a } has no solution.

For a given unification problem E, a set S of unifiers is called complete if each solution substitution is subsumed by some substitution in S. A complete substitution set always exists (e.g. the set of all solutions), but in some frameworks (such as unrestricted higher-order unification) the problem of determining whether any solution exists (i.e., whether the complete substitution set is nonempty) is undecidable.

The set S is called minimal if none of its members subsumes another one. Depending on the framework, a complete and minimal substitution set may have zero, one, finitely many, or infinitely many members, or may not exist at all due to an infinite chain of redundant members.^[9] Thus, in general, unification algorithms compute a finite approximation of the complete set, which may or may not be minimal, although most algorithms avoid redundant unifiers when possible.^[7] For first-order syntactical unification, Martelli and Montanari^[10] gave an algorithm that reports unsolvability or computes a single unifier that by itself forms a complete and minimal substitution set, called the most general unifier.

Syntactic unification of first-order terms

Schematic triangle diagram of syntactically unifying terms t₁ and t₂ by a substitution σ

Syntactic unification of first-order terms is the most widely used unification framework. It is based on T being the set of first-order terms (over some given set V of variables, C of constants and F_n of n-ary function symbols) and on ≡ being syntactic equality. In this framework, each solvable unification problem {l₁ ≐ r₁, ..., l_n ≐ r_n} has a complete, and obviously minimal, singleton solution set {σ}. Its member σ is called the most general unifier (mgu) of the problem. The terms on the left and the right hand side of each potential equation become syntactically equal when the mgu is applied i.e. l₁σ = r₁σ ∧ ... ∧ l_nσ = r_nσ. Any unifier of the problem is subsumed^{[note 4]} by the mgu σ. The mgu is unique up to variants: if S₁ and S₂ are both complete and minimal solution sets of the same syntactical unification problem, then S₁ = { σ₁ } and S₂ = { σ₂ } for some substitutions σ₁ and σ₂, and xσ₁ is a variant of xσ₂ for each variable x occurring in the problem.

For example, the unification problem { x ≐ z, y ≐ f(x) } has a unifier { x ↦ z, y ↦ f(z) }, because

x	{ x ↦ z, y ↦ f(z) }	=	z	=	z	{ x ↦ z, y ↦ f(z) }	, and
y	{ x ↦ z, y ↦ f(z) }	=	f(z)	=	f(x)	{ x ↦ z, y ↦ f(z) }	.

This is also the most general unifier. Other unifiers for the same problem are e.g. { x ↦ f(x₁), y ↦ f(f(x₁)), z ↦ f(x₁) }, { x ↦ f(f(x₁)), y ↦ f(f(f(x₁))), z ↦ f(f(x₁)) }, and so on; there are infinitely many similar unifiers.

As another example, the problem g(x,x) ≐ f(y) has no solution with respect to ≡ being literal identity, since any substitution applied to the left and right hand side will keep the outermost g and f, respectively, and terms with different outermost function symbols are syntactically different.

A unification algorithm

The first algorithm given by Robinson (1965) was rather inefficient; cf. box. The following faster algorithm originated from Martelli, Montanari (1982).^{[note 5]} This paper also lists preceding attempts to find an efficient syntactical unification algorithm,^{[14][15][16][17][18][19]} and states that linear-time algorithms were discovered independently by Martelli, Montanari (1976)^[16] and Paterson, Wegman (1976,^[20] 1978^[17]).^{[note 6]}

Given a finite set [math]\displaystyle{ G = \{ s_1 \doteq t_1, ..., s_n \doteq t_n \} }[/math] of potential equations, the algorithm applies rules to transform it to an equivalent set of equations of the form { x₁ ≐ u₁, ..., x_m ≐ u_m } where x₁, ..., x_m are distinct variables and u₁, ..., u_m are terms containing none of the x_i. A set of this form can be read as a substitution. If there is no solution the algorithm terminates with ⊥; other authors use "Ω", or "fail" in that case. The operation of substituting all occurrences of variable x in problem G with term t is denoted G {x ↦ t}. For simplicity, constant symbols are regarded as function symbols having zero arguments.

[math]\displaystyle{ G \cup \{ t \doteq t \} }[/math]	[math]\displaystyle{ \Rightarrow }[/math]	[math]\displaystyle{ G }[/math]		delete
[math]\displaystyle{ G \cup \{ f(s_0, ..., s_k) \doteq f(t_0, ..., t_k) \} }[/math]	[math]\displaystyle{ \Rightarrow }[/math]	[math]\displaystyle{ G \cup \{ s_0 \doteq t_0, ..., s_k \doteq t_k \} }[/math]		decompose
[math]\displaystyle{ G \cup \{ f(s_0, \ldots,s_k) \doteq g(t_0,...,t_m) \} }[/math]	[math]\displaystyle{ \Rightarrow }[/math]	[math]\displaystyle{ \bot }[/math]	if [math]\displaystyle{ f \neq g }[/math] or [math]\displaystyle{ k \neq m }[/math]	conflict
[math]\displaystyle{ G \cup \{ f(s_0,...,s_k) \doteq x \} }[/math]	[math]\displaystyle{ \Rightarrow }[/math]	[math]\displaystyle{ G \cup \{ x \doteq f(s_0,...,s_k) \} }[/math]		swap
[math]\displaystyle{ G \cup \{ x \doteq t \} }[/math]	[math]\displaystyle{ \Rightarrow }[/math]	[math]\displaystyle{ G\{x \mapsto t\} \cup \{ x \doteq t \} }[/math]	if [math]\displaystyle{ x \not\in \text{vars}(t) }[/math] and [math]\displaystyle{ x \in \text{vars}(G) }[/math]	eliminate[note 7]
[math]\displaystyle{ G \cup \{ x \doteq f(s_0,...,s_k) \} }[/math]	[math]\displaystyle{ \Rightarrow }[/math]	[math]\displaystyle{ \bot }[/math]	if [math]\displaystyle{ x \in \text{vars}(f(s_0,...,s_k)) }[/math]	check

Occurs check

Main page: Occurs check

An attempt to unify a variable x with a term containing x as a strict subterm x ≐ f(..., x, ...) would lead to an infinite term as solution for x, since x would occur as a subterm of itself. In the set of (finite) first-order terms as defined above, the equation x ≐ f(..., x, ...) has no solution; hence the eliminate rule may only be applied if x ∉ vars(t). Since that additional check, called occurs check, slows down the algorithm, it is omitted e.g. in most Prolog systems. From a theoretical point of view, omitting the check amounts to solving equations over infinite trees, see #Unification of infinite terms below.

Proof of termination

For the proof of termination of the algorithm consider a triple [math]\displaystyle{ \langle n_{var}, n_{lhs}, n_{eqn}\rangle }[/math] where n_var is the number of variables that occur more than once in the equation set, n_lhs is the number of function symbols and constants on the left hand sides of potential equations, and n_eqn is the number of equations. When rule eliminate is applied, n_var decreases, since x is eliminated from G and kept only in { x ≐ t }. Applying any other rule can never increase n_var again. When rule decompose, conflict, or swap is applied, n_lhs decreases, since at least the left hand side's outermost f disappears. Applying any of the remaining rules delete or check can't increase n_lhs, but decreases n_eqn. Hence, any rule application decreases the triple [math]\displaystyle{ \langle n_{var}, n_{lhs}, n_{eqn}\rangle }[/math] with respect to the lexicographical order, which is possible only a finite number of times.

Conor McBride observes^[21] that "by expressing the structure which unification exploits" in a dependently typed language such as Epigram, Robinson's unification algorithm can be made recursive on the number of variables, in which case a separate termination proof becomes unnecessary.

Examples of syntactic unification of first-order terms

In the Prolog syntactical convention a symbol starting with an upper case letter is a variable name; a symbol that starts with a lowercase letter is a function symbol; the comma is used as the logical and operator. For mathematical notation, x,y,z are used as variables, f,g as function symbols, and a,b as constants.

Two terms with an exponentially larger tree for their least common instance. Its dag representation (rightmost, orange part) is still of linear size.

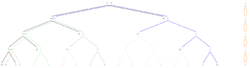
The most general unifier of a syntactic first-order unification problem of size n may have a size of 2ⁿ. For example, the problem [math]\displaystyle{ (((a*z)*y)*x)*w \doteq w*(x*(y*(z*a))) }[/math] has the most general unifier [math]\displaystyle{ \{ z \mapsto a, y \mapsto a*a, x \mapsto (a*a)*(a*a), w \mapsto ((a*a)*(a*a))*((a*a)*(a*a)) \} }[/math], cf. picture. In order to avoid exponential time complexity caused by such blow-up, advanced unification algorithms work on directed acyclic graphs (dags) rather than trees.^[22]

Application: unification in logic programming

The concept of unification is one of the main ideas behind logic programming, best known through the language Prolog. It represents the mechanism of binding the contents of variables and can be viewed as a kind of one-time assignment. In Prolog, this operation is denoted by the equality symbol =, but is also done when instantiating variables (see below). It is also used in other languages by the use of the equality symbol =, but also in conjunction with many operations including +, -, *, /. Type inference algorithms are typically based on unification.

In Prolog:

1. A variable can be unified with a constant, a term, or another variable, thus effectively becoming its alias. In many modern Prolog dialects and in first-order logic, a variable cannot be unified with a term that contains it; this is the so-called occurs check.
2. Two constants can be unified only if they are identical.
3. Similarly, a term can be unified with another term if the top function symbols and arities of the terms are identical and if the parameters can be unified simultaneously. Note that this is a recursive behavior.

Application: type inference

Unification is used during type inference for languages with type systems based on Hindley-Milner, including the functional languages Haskell and ML. On one hand, the programmer does not need to provide type information for every function, on the other hand it is used to detect typing errors. The Haskell expression True : ['x', 'y', 'z'] is not correctly typed. The list construction function (:) is of type a -> [a] -> [a], and for the first argument True the polymorphic type variable a has to be unified with True's type, Bool. The second argument, ['x', 'y', 'z'], is of type [Char], but a cannot be both Bool and Char at the same time.

Like for Prolog, an algorithm for type inference can be given:

1. Any type variable unifies with any type expression, and is instantiated to that expression. A specific theory might restrict this rule with an occurs check.
2. Two type constants unify only if they are the same type.
3. Two type constructions unify only if they are applications of the same type constructor and all of their component types recursively unify.

Application: Feature Structure Unification

Unification has been used in different research areas of computational linguistics.^[23][24]

Order-sorted unification

Order-sorted logic allows one to assign a sort, or type, to each term, and to declare a sort s₁ a subsort of another sort s₂, commonly written as s₁ ⊆ s₂. For example, when reаsoning about biological creatures, it is useful to declare a sort dog to be a subsort of a sort animal. Wherever a term of some sort s is required, a term of any subsort of s may be supplied instead. For example, assuming a function declaration mother: animal → animal, and a constant declaration lassie: dog, the term mother(lassie) is perfectly valid and has the sort animal. In order to supply the information that the mother of a dog is a dog in turn, another declaration mother: dog → dog may be issued; this is called function overloading, similar to overloading in programming languages.

Walther gave a unification algorithm for terms in order-sorted logic, requiring for any two declared sorts s₁, s₂ their intersection s₁ ∩ s₂ to be declared, too: if x₁ and x₂ is a variable of sort s₁ and s₂, respectively, the equation x₁ ≐ x₂ has the solution { x₁ = x, x₂ = x }, where x: s₁ ∩ s₂. ^[25] After incorporating this algorithm into a clause-based automated theorem prover, he could solve a benchmark problem by translating it into order-sorted logic, thereby boiling it down an order of magnitude, as many unary predicates turned into sorts.

Smolka generalized order-sorted logic to allow for parametric polymorphism. ^[26] In his framework, subsort declarations are propagated to complex type expressions. As a programming example, a parametric sort list(X) may be declared (with X being a type parameter as in a C++ template), and from a subsort declaration int ⊆ float the relation list(int) ⊆ list(float) is automatically inferred, meaning that each list of integers is also a list of floats.

Schmidt-Schauß generalized order-sorted logic to allow for term declarations. ^[27] As an example, assuming subsort declarations even ⊆ int and odd ⊆ int, a term declaration like ∀ i : int. (i + i) : even allows to declare a property of integer addition that could not be expressed by ordinary overloading.

Unification of infinite terms

Background on infinite trees:

• B. Courcelle (1983). "Fundamental Properties of Infinite Trees". Theoret. Comput. Sci. 25 (2): 95–169. doi:10.1016/0304-3975(83)90059-2. 
• Michael J. Maher (Jul 1988). "Complete Axiomatizations of the Algebras of Finite, Rational and Infinite Trees". Proc. IEEE 3rd Annual Symp. on Logic in Computer Science, Edinburgh. pp. 348–357. 
• Joxan Jaffar; Peter J. Stuckey (1986). "Semantics of Infinite Tree Logic Programming". Theoretical Computer Science 46: 141–158. doi:10.1016/0304-3975(86)90027-7. 

Unification algorithm, Prolog II:

• A. Colmerauer (1982). Prolog and Infinite Trees. Academic Press. 
• Alain Colmerauer (1984). "Equations and Inequations on Finite and Infinite Trees". in ICOT. Proc. Int. Conf. on Fifth Generation Computer Systems. pp. 85–99. 

Applications:

• Francis Giannesini; Jacques Cohen (1984). "Parser Generation and Grammar Manipulation using Prolog's Infinite Trees". Journal of Logic Programming 1 (3): 253–265. doi:10.1016/0743-1066(84)90013-X. 

E-unification

E-unification is the problem of finding solutions to a given set of equations, taking into account some equational background knowledge E. The latter is given as a set of universal equalities. For some particular sets E, equation solving algorithms (a.k.a. E-unification algorithms) have been devised; for others it has been proven that no such algorithms can exist.

For example, if a and b are distinct constants, the equation [math]\displaystyle{ x * a \doteq y * b }[/math] has no solution with respect to purely syntactic unification, where nothing is known about the operator [math]\displaystyle{ * }[/math]. However, if the [math]\displaystyle{ * }[/math] is known to be commutative, then the substitution {x ↦ b, y ↦ a} solves the above equation, since

	[math]\displaystyle{ x * a }[/math]	{x ↦ b, y ↦ a}
=	[math]\displaystyle{ b * a }[/math]		by substitution application
=	[math]\displaystyle{ a * b }[/math]		by commutativity of [math]\displaystyle{ * }[/math]
=	[math]\displaystyle{ y * b }[/math]	{x ↦ b, y ↦ a}	by (converse) substitution application

The background knowledge E could state the commutativity of [math]\displaystyle{ * }[/math] by the universal equality "[math]\displaystyle{ u * v = v * u }[/math] for all u, v".

Particular background knowledge sets E

It is said that unification is decidable for a theory, if a unification algorithm has been devised for it that terminates for any input problem. It is said that unification is semi-decidable for a theory, if a unification algorithm has been devised for it that terminates for any solvable input problem, but may keep searching forever for solutions of an unsolvable input problem.

Unification is decidable for the following theories:

• A^[28]
• A,C^[29]
• A,C,I^[30]
• A,C,N_l^{[note 8][30]}
• A,I^[31]
• A,N_l,N_r (monoid)^[32]
• C^[33]
• Boolean rings^[34][35]
• Abelian groups, even if the signature is expanded by arbitrary additional symbols (but not axioms)^[36]
• K4 modal algebras^[37]

Unification is semi-decidable for the following theories:

• A,D_l,D_r^[38]
• A,C,D_l^{[note 8][39]}
• Commutative rings^[36]

One-sided paramodulation

If there is a convergent term rewriting system R available for E, the one-sided paramodulation algorithm^[40] can be used to enumerate all solutions of given equations.

Starting with G being the unification problem to be solved and S being the identity substitution, rules are applied nondeterministically until the empty set appears as the actual G, in which case the actual S is a unifying substitution. Depending on the order the paramodulation rules are applied, on the choice of the actual equation from G, and on the choice of R's rules in mutate, different computations paths are possible. Only some lead to a solution, while others end at a G ≠ {} where no further rule is applicable (e.g. G = { f(...) ≐ g(...) }).

For an example, a term rewrite system R is used defining the append operator of lists built from cons and nil; where cons(x,y) is written in infix notation as x.y for brevity; e.g. app(a.b.nil,c.d.nil) → a.app(b.nil,c.d.nil) → a.b.app(nil,c.d.nil) → a.b.c.d.nil demonstrates the concatenation of the lists a.b.nil and c.d.nil, employing the rewrite rule 2,2, and 1. The equational theory E corresponding to R is the congruence closure of R, both viewed as binary relations on terms. For example, app(a.b.nil,c.d.nil) ≡ a.b.c.d.nil ≡ app(a.b.c.d.nil,nil). The paramodulation algorithm enumerates solutions to equations with respect to that E when fed with the example R.

A successful example computation path for the unification problem { app(x,app(y,x)) ≐ a.a.nil } is shown below. To avoid variable name clashes, rewrite rules are consistently renamed each time before their use by rule mutate; v₂, v₃, ... are computer-generated variable names for this purpose. In each line, the chosen equation from G is highlighted in red. Each time the mutate rule is applied, the chosen rewrite rule (1 or 2) is indicated in parentheses. From the last line, the unifying substitution S = { y ↦ nil, x ↦ a.nil } can be obtained. In fact, app(x,app(y,x)) {y↦nil, x↦ a.nil } = app(a.nil,app(nil,a.nil)) ≡ app(a.nil,a.nil) ≡ a.app(nil,a.nil) ≡ a.a.nil solves the given problem. A second successful computation path, obtainable by choosing "mutate(1), mutate(2), mutate(2), mutate(1)" leads to the substitution S = { y ↦ a.a.nil, x ↦ nil }; it is not shown here. No other path leads to a success.

Narrowing

Triangle diagram of narrowing step s ↝ t at position p in term s, with unifying substitution σ (bottom row), using a rewrite rule l → r (top row)

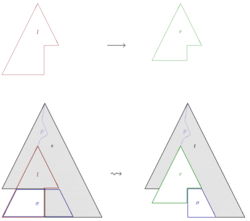
If R is a convergent term rewriting system for E, an approach alternative to the previous section consists in successive application of "narrowing steps"; this will eventually enumerate all solutions of a given equation. A narrowing step (cf. picture) consists in

• choosing a nonvariable subterm of the current term,
• syntactically unifying it with the left hand side of a rule from R, and
• replacing the instantiated rule's right hand side into the instantiated term.

Formally, if l → r is a renamed copy of a rewrite rule from R, having no variables in common with a term s, and the subterm s|_p is not a variable and is unifiable with l via the mgu σ, then s can be narrowed to the term t = sσ[rσ]_p, i.e. to the term sσ, with the subterm at p replaced by rσ. The situation that s can be narrowed to t is commonly denoted as s ↝ t. Intuitively, a sequence of narrowing steps t₁ ↝ t₂ ↝ ... ↝ t_n can be thought of as a sequence of rewrite steps t₁ → t₂ → ... → t_n, but with the initial term t₁ being further and further instantiated, as necessary to make each of the used rules applicable.

The above example paramodulation computation corresponds to the following narrowing sequence ("↓" indicating instantiation here):

The last term, v₂.v₂.nil can be syntactically unified with the original right hand side term a.a.nil.

The narrowing lemma^[41] ensures that whenever an instance of a term s can be rewritten to a term t by a convergent term rewriting system, then s and t can be narrowed and rewritten to a term s′ and t′, respectively, such that t′ is an instance of s′.

Formally: whenever sσ →∗ t holds for some substitution σ, then there exist terms s′, t′ such that s ↝∗ s′ and t →∗ t′ and s′ τ = t′ for some substitution τ.

Higher-order unification

In Goldfarb's^[42] reduction of Hilbert's 10th problem to second-order unifiability, the equation [math]\displaystyle{ X_1 * X_2 = X_3 }[/math] corresponds to the depicted unification problem, with function variables [math]\displaystyle{ F_i }[/math] corresponding to [math]\displaystyle{ X_i }[/math] and [math]\displaystyle{ G }[/math] fresh.

Many applications require one to consider the unification of typed lambda-terms instead of first-order terms. Such unification is often called higher-order unification. Higher-order unification is undecidable,^[42][43][44] and such unification problems do not have most general unifiers. For example, the unification problem { f(a,b,a) ≐ d(b,a,c) }, where the only variable is f, has the solutions {f ↦ λx.λy.λz. d(y,x,c) }, {f ↦ λx.λy.λz. d(y,z,c) }, {f ↦ λx.λy.λz. d(y,a,c) }, {f ↦ λx.λy.λz. d(b,x,c) }, {f ↦ λx.λy.λz. d(b,z,c) } and {f ↦ λx.λy.λz. d(b,a,c) }. A well studied branch of higher-order unification is the problem of unifying simply typed lambda terms modulo the equality determined by αβη conversions. Gérard Huet gave a semi-decidable (pre-)unification algorithm^[45] that allows a systematic search of the space of unifiers (generalizing the unification algorithm of Martelli-Montanari^[10] with rules for terms containing higher-order variables) that seems to work sufficiently well in practice. Huet^[46] and Gilles Dowek^[47] have written articles surveying this topic.

Several subsets of higher-order unification are well-behaved, in that they are decidable and have a most-general unifier for solvable problems. One such subset is the previously described first-order terms. Higher-order pattern unification, due to Dale Miller,^[48] is another such subset. The higher-order logic programming languages λProlog and Twelf have switched from full higher-order unification to implementing only the pattern fragment; surprisingly pattern unification is sufficient for almost all programs, if each non-pattern unification problem is suspended until a subsequent substitution puts the unification into the pattern fragment. A superset of pattern unification called functions-as-constructors unification is also well-behaved.^[49] The Zipperposition theorem prover has an algorithm integrating these well-behaved subsets into a full higher-order unification algorithm.^[7]

In computational linguistics, one of the most influential theories of elliptical construction is that ellipses are represented by free variables whose values are then determined using Higher-Order Unification. For instance, the semantic representation of "Jon likes Mary and Peter does too" is like(j, m) ∧ R(p) and the value of R (the semantic representation of the ellipsis) is determined by the equation like(j, m) = R(j) . The process of solving such equations is called Higher-Order Unification.^[50]

Wayne Snyder gave a generalization of both higher-order unification and E-unification, i.e. an algorithm to unify lambda-terms modulo an equational theory.^[51]

See also

• Rewriting
• Admissible rule
• Explicit substitution in lambda calculus
• Mathematical equation solving
• Dis-unification: solving inequations between symbolic expression
• Anti-unification: computing a least general generalization (lgg) of two terms, dual to computing a most general instance (mgu)
• Subsumption lattice, a lattice having unification as meet and anti-unification as join
• Ontology alignment (use unification with semantic equivalence)

Notes

References

Further reading

• Franz Baader and Wayne Snyder (2001). "Unification Theory" . In John Alan Robinson and Andrei Voronkov, editors, Handbook of Automated Reasoning, volume I, pages 447–533. Elsevier Science Publishers.^{[|permanent dead link|dead link}}]}
• Gilles Dowek (2001). "Higher-order Unification and Matching" . In Handbook of Automated Reasoning.
• Franz Baader and Tobias Nipkow (1998). Term Rewriting and All That. Cambridge University Press.
• Franz Baader and Jörg H. Siekmann (de) (1993). "Unification Theory". In Handbook of Logic in Artificial Intelligence and Logic Programming.
• Jean-Pierre Jouannaud and Claude Kirchner (1991). "Solving Equations in Abstract Algebras: A Rule-Based Survey of Unification". In Computational Logic: Essays in Honor of Alan Robinson.
• Nachum Dershowitz and Jean-Pierre Jouannaud, Rewrite Systems, in: Jan van Leeuwen (ed.), Handbook of Theoretical Computer Science, volume B Formal Models and Semantics, Elsevier, 1990, pp. 243–320
• Jörg H. Siekmann (1990). "Unification Theory". In Claude Kirchner (editor) Unification. Academic Press.
• Kevin Knight (Mar 1989). "Unification: A Multidisciplinary Survey". ACM Computing Surveys 21 (1): 93–124. doi:10.1145/62029.62030. http://www.isi.edu/natural-language/people/unification-knight.pdf. 
• Gérard Huet and Derek C. Oppen (1980). "Equations and Rewrite Rules: A Survey". Technical report. Stanford University.
• Raulefs, Peter; Siekmann, Jörg; Szabó, P.; Unvericht, E. (1979). "A short survey on the state of the art in matching and unification problems". ACM SIGSAM Bulletin 13 (2): 14–20. doi:10.1145/1089208.1089210. 
• Claude Kirchner and Hélène Kirchner. Rewriting, Solving, Proving. In preparation.

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Unification (computer science). Read more