Variation of information

In probability theory and information theory, the variation of information or shared information distance is a measure of the distance between two clusterings (partitions of elements). It is closely related to mutual information; indeed, it is a simple linear expression involving the mutual information. Unlike the mutual information, however, the variation of information is a true metric, in that it obeys the triangle inequality.^[1][2][3]

Information diagram illustrating the relation between information entropies, mutual information and variation of information.

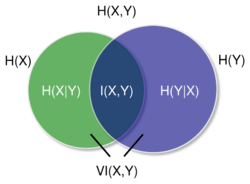
Definition

Suppose we have two partitions ${\displaystyle X}$ and ${\displaystyle Y}$ of a set ${\displaystyle A}$ into disjoint subsets, namely ${\displaystyle X=\{X_1,X_2,\dots ,X_k\}}$ and ${\displaystyle Y=\{Y_1,Y_2,\dots ,Y_l\}}$.

Let:

${\displaystyle n=\sum _i|X_i|=\sum _j|Y_j|=|A|}$

${\displaystyle p_i=|X_i|/n}$ and ${\displaystyle q_j=|Y_j|/n}$

${\displaystyle r_{ij}=|X_i\cap Y_j|/n}$

Then the variation of information between the two partitions is:

${\displaystyle \mathrm{VI}(X;Y)=-\sum _{i,j}{r}_{ij}[\log (r_{ij}/p_i)+\log (r_{ij}/q_j)]}$.

This is equivalent to the shared information distance between the random variables i and j with respect to the uniform probability measure on ${\displaystyle A}$ defined by ${\displaystyle \mu (B):=|B|/n}$ for ${\displaystyle B\subseteq A}$.

Explicit information content

We can rewrite this definition in terms that explicitly highlight the information content of this metric.

The set of all partitions of a set form a compact Lattice where the partial order induces two operations, the meet ${\displaystyle \wedge }$ and the join ${\displaystyle \vee }$, where the maximum ${\displaystyle \bar{1}}$ is the partition with only one block, i.e., all elements grouped together, and the minimum is ${\displaystyle \bar{0}}$, the partition consisting of all elements as singletons. The meet of two partitions ${\displaystyle X}$ and ${\displaystyle Y}$ is easy to understand as that partition formed by all pair intersections of one block of, ${\displaystyle X_i}$, of ${\displaystyle X}$ and one, ${\displaystyle Y_i}$, of ${\displaystyle Y}$. It then follows that ${\displaystyle X\wedge Y\subseteq X}$ and ${\displaystyle X\wedge Y\subseteq Y}$.

Let's define the entropy of a partition ${\displaystyle X}$ as

where ${\displaystyle p_i=|X_i|/n}$. Clearly, ${\displaystyle H(\bar{1})=0}$ and ${\displaystyle H(\bar{0})=\log n}$. The entropy of a partition is a monotonous function on the lattice of partitions in the sense that ${\displaystyle X\subseteq Y\Rightarrow H(X)\ge H(Y)}$.

Then the VI distance between ${\displaystyle X}$ and ${\displaystyle Y}$ is given by

The difference ${\displaystyle d(X,Y)\equiv |H\left(X\right)-H\left(Y\right)|}$ is a pseudo-metric as ${\displaystyle d(X,Y)=0}$ doesn't necessarily imply that ${\displaystyle X=Y}$. From the definition of ${\displaystyle \bar{1}}$, it is ${\displaystyle \mathrm{VI}(X,1)=H\left(X\right)}$.

If in the Hasse diagram we draw an edge from every partition to the maximum ${\displaystyle \bar{1}}$ and assign it a weight equal to the VI distance between the given partition and ${\displaystyle \bar{1}}$, we can interpret the VI distance as basically an average of differences of edge weights to the maximum

For ${\displaystyle H(X)}$ as defined above, it holds that the joint information of two partitions coincides with the entropy of the meet

and we also have that ${\displaystyle d(X,X\wedge Y)=H(X\wedge Y|X)}$ coincides with the conditional entropy of the meet (intersection) ${\displaystyle X\wedge Y}$ relative to ${\displaystyle X}$.

Identities

The variation of information satisfies

${\displaystyle \mathrm{VI}(X;Y)=H(X)+H(Y)-2I(X,Y)}$,

where ${\displaystyle H(X)}$ is the entropy of ${\displaystyle X}$, and ${\displaystyle I(X,Y)}$ is mutual information between ${\displaystyle X}$ and ${\displaystyle Y}$ with respect to the uniform probability measure on ${\displaystyle A}$. This can be rewritten as

${\displaystyle \mathrm{VI}(X;Y)=H(X,Y)-I(X,Y)}$,

where ${\displaystyle H(X,Y)}$ is the joint entropy of ${\displaystyle X}$ and ${\displaystyle Y}$, or

${\displaystyle \mathrm{VI}(X;Y)=H(X|Y)+H(Y|X)}$,

where ${\displaystyle H(X|Y)}$ and ${\displaystyle H(Y|X)}$ are the respective conditional entropies.

The variation of information can also be bounded, either in terms of the number of elements:

${\displaystyle \mathrm{VI}(X;Y)\le \log (n)}$,

Or with respect to a maximum number of clusters, ${\displaystyle K^{\ast }}$:

${\displaystyle \mathrm{VI}(X;Y)\le 2\log (K^{\ast })}$

Triangle inequality

To verify the triangle inequality ${\displaystyle \mathrm{VI}(X;Z)\le \mathrm{VI}(X;Y)+\mathrm{VI}(Y;Z)}$, expand using the identity ${\displaystyle \mathrm{VI}(X;Y)=H(X|Y)+H(Y|X)}$. It simplifies to ${\displaystyle H(X|Z)\le H(X|Y)+H(Y|Z)}$The right side equals ${\displaystyle H(X,Y|Z)}$, which is no less than the left side. This is intuitive, as ${\displaystyle X,Y|Z}$ contains no less randomness than ${\displaystyle X|Z}$.

References

Further reading

• Arabie, P.; Boorman, S. A. (1973). "Multidimensional scaling of measures of distance between partitions". Journal of Mathematical Psychology 10 (2): 148–203. doi:10.1016/0022-2496(73)90012-6. 
• Meila, Marina (2003). "Comparing Clusterings by the Variation of Information". Learning Theory and Kernel Machines. Lecture Notes in Computer Science 2777: 173–187. doi:10.1007/978-3-540-45167-9_14. ISBN 978-3-540-40720-1. 
• Meila, M. (2007). "Comparing clusterings—an information based distance". Journal of Multivariate Analysis 98 (5): 873–895. doi:10.1016/j.jmva.2006.11.013. 
• Kingsford, Carl (2009). "Information Theory Notes". http://www.cs.umd.edu/class/spring2009/cmsc858l/InfoTheoryHints.pdf. 
• Kraskov, Alexander; Harald Stögbauer; Ralph G. Andrzejak; Peter Grassberger (2003). "Hierarchical Clustering Based on Mutual Information". arXiv:q-bio/0311039.

External links

• Partanalyzer includes a C++ implementation of VI and other metrics and indices for analyzing partitions and clusterings
• C++ implementation with MATLAB mex files

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Variation of information. Read more