Wu–Yang dictionary

In topology and high energy physics, the Wu–Yang dictionary refers to the mathematical identification that allows back-and-forth translation between the concepts of gauge theory and those of differential geometry. It was devised by Tai Tsun Wu and C. N. Yang in 1975 when studying the relation between electromagnetism and fiber bundle theory.^[1] This dictionary has been credited as bringing mathematics and theoretical physics closer together.^[2]

A crucial example of the success of the dictionary is that it allowed the understanding of monopole quantization in terms of Hopf fibrations.^[3][4]

History

In 1931, Paul Dirac published his quantization conditions for magnetic monopoles. Unaware of any connection, the same year, mathematician Heinz Hopf independently proposed his epynomous fibration of a 3-sphere.^[4]

Equivalences between fiber bundle theory and gauge theory were hinted at the end of the 1960s. In 1967, mathematician Andrzej Trautman started a series of lectures aimed at physicists and mathematicians at King's College London regarding these connections.^[4]

Theoretical physicists Tsun Wu and C. N. Yang working in Stony Brook University, published a paper in 1975 on the mathematical framework of electromagnetism and the Aharonov–Bohm effect in terms of fiber bundles. A year later, mathematician Isadore Singer came to visit and brought a copy back to the University of Oxford.^[2][5][6] Singer showed the paper to Michael Atiyah and other mathematicians, sparking a close collaboration between physicists and mathematicians.^[2]

Yang also recounts a conversation that he had with one of the mathematicians that founded fiber bundle theory, Shiing-Shen Chern:^[2]

In 1975, impressed with the fact that gauge fields are connections on fiber bundles, I drove to the house of Shiing-Shen Chern in El Cerrito, near Berkeley. (I had taken courses with him in the early 1940s when he was a young professor and I an undergraduate student at the National Southwest Associated University in Kunming, China . That was before fiber bundles had become important in differential geometry and before Chern had made history with his contributions to the generalized Gauss–Bonnet theorem and the Chern classes.) We had much to talk about: friends, relatives, China. When our conversation turned to fiber bundles, I told him that I had finally learned from Jim Simons the beauty of fiber-bundle theory and the profound Chern-Weil theorem. I said I found it amazing that gauge fields are exactly connections on fiber bundles, which the mathematicians developed without reference to the physical world. I added ‘this is both thrilling and puzzling, since you mathematicians dreamed up these concepts out of nowhere.’ He immediately protested, ‘No, no. These concepts were not dreamed up. They were natural and real.'

Using these equivalences, Trautman demonstrated an equivalence between Dirac quantization condition and Hopf fibration in 1977.^[4] Mathematician Jim Simons discussing this equivalence with Yang expressed that “Dirac had discovered trivial and nontrivial bundles before mathematicians.”^[4]

Description

Summarized version

The Wu-Yang dictionary relates terms in particle physics with terms in mathematics, specifically fiber bundle theory. Many versions and generalization of the dictionary exist. Here is an example of a dictionary, which puts each physics term next to its mathematical analogue:^[7]

Original version for electromagnetism

Aharonov-Bohm experiment: electrons pass around a cylinder where there is a non-zero magnetic field. Outside the cylinder the field strength is 0.

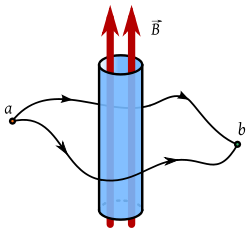
Wu and Yang considered the description of an electron traveling around a cylinder in the presence of a magnetic field inside the cylinder (outside the cylinder the field vanishes i.e. [math]\displaystyle{ f_{\mu\nu}=0 }[/math]). According to the Aharonov–Bohm effect, the interference patterns shift by a factor [math]\displaystyle{ \exp(-i \Omega/\Omega_0) }[/math], where [math]\displaystyle{ \Omega }[/math] is the magnetic flux and [math]\displaystyle{ \Omega_0 }[/math] is the magnetic flux quantum. For two different fluxes a and b, the results are identical if [math]\displaystyle{ \Omega_a-\Omega_b=N\Omega_0 }[/math], where [math]\displaystyle{ N }[/math] is an integer. We define the operator [math]\displaystyle{ S_{ab} }[/math] as the operator that brings the electron wave function from one configuration to the other [math]\displaystyle{ \psi_b=S_{ba}\psi_a }[/math]. For an electron that takes a path from point P to point Q, we define the phase factor as

[math]\displaystyle{ \Phi_{PQ} =\exp \left(-\frac{i}{\Omega_0} \int_P^Q A_\mu \mathrm{d} x^{\mu}\right) }[/math],

where [math]\displaystyle{ A_\mu }[/math] is the electromagnetic four-potential. For the case of a SU₂ gauge field, we can make the substitution

[math]\displaystyle{ A_\mu=ib_\mu^kX_k }[/math],

where [math]\displaystyle{ X_k=-i\sigma_k/2 }[/math] are the generators of SU₂, [math]\displaystyle{ \sigma_k }[/math] are the Pauli matrices. Under these concepts, Wu and Yang showed the relation between the language of gauge theory and fiber bundles, was codified in following dictionary:^[2][8][9]

See also

• 't Hooft–Polyakov monopole
• Wu–Yang monopole

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Wu–Yang dictionary. Read more