Applications of quantum mechanics

Quantum physics is a branch of modern physics in which energy and matter are described at their most fundamental level, that of energy quanta, elementary particles, and quantum fields. Quantum physics encompasses any discipline concerned with systems that exhibit notable quantum-mechanical effects, where waves have properties of particles, and particles behave like waves. Applications of quantum mechanics include explaining phenomena found in nature as well as developing technologies that rely upon quantum effects, like integrated circuits and lasers.^{[note 1]}

Quantum mechanics is also critically important for understanding how individual atoms are joined by covalent bonds to form molecules. The application of quantum mechanics to chemistry is known as quantum chemistry. Quantum mechanics can also provide quantitative insight into ionic and covalent bonding processes by explicitly showing which molecules are energetically favorable to which others and the magnitudes of the energies involved.^[1]

Historically, the first applications of quantum mechanics to physical systems were the algebraic determination of the hydrogen spectrum by Wolfgang Pauli^[2] and the treatment of diatomic molecules by Lucy Mensing.^[3]

In many aspects modern technology operates at a scale where quantum effects are significant. Important applications of quantum theory include quantum chemistry, quantum optics, quantum computing, superconducting magnets, light-emitting diodes, the optical amplifier and the laser, the transistor and semiconductors such as the microprocessor, medical and research imaging such as magnetic resonance imaging and electron microscopy.^[4] Explanations for many biological and physical phenomena are rooted in the nature of the chemical bond, most notably the macro-molecule DNA.

Many modern electronic devices are designed using quantum mechanics. Examples include lasers, electron microscopes, magnetic resonance imaging (MRI) devices and the components used in computing hardware. The study of semiconductors led to the invention of the diode and the transistor, which are indispensable parts of modern electronics systems, computer and telecommunications devices. Another application is for making laser diodes and light-emitting diodes, which are a high-efficiency source of light. The global positioning system (GPS) makes use of atomic clocks to measure precise time differences and therefore determine a user's location.

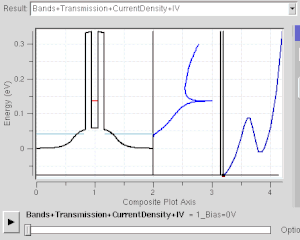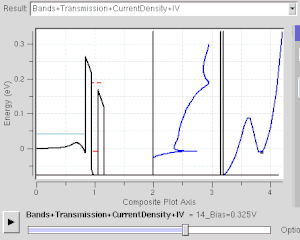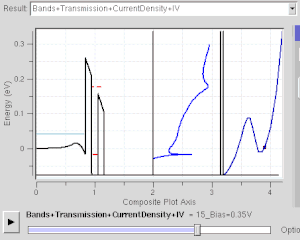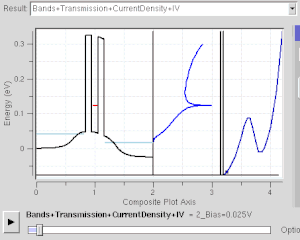
Many electronic devices operate using the effect of quantum tunneling. Flash memory chips found in USB drives use quantum tunneling to erase their memory cells. Some negative differential resistance devices also utilize the quantum tunneling effect, such as resonant tunneling diodes. Unlike classical diodes, its current is carried by resonant tunneling through two or more potential barriers (see figure at right). Its negative resistance behavior can only be understood with quantum mechanics: As the confined state moves close to Fermi level, tunnel current increases. As it moves away, the current decreases. Quantum mechanics is necessary to understand and design such electronic devices.

Many scientists are currently seeking robust methods of directly manipulating quantum states. Efforts are being made to more fully develop quantum cryptography, which will theoretically allow guaranteed secure transmission of information.

An inherent advantage yielded by quantum cryptography when compared to classical cryptography is the detection of passive eavesdropping. This is a natural result of the behavior of quantum bits; due to the observer effect, if a bit in a superposition state were to be observed, the superposition state would collapse into an eigenstate. Because the intended recipient was expecting to receive the bit in a superposition state, the intended recipient would know there was an attack, because the bit's state would no longer be in a superposition.^[5]

Another goal is the development of quantum computers, which are expected to perform certain computational tasks exponentially faster than classical computers. Instead of using classical bits, quantum computers use qubits, which can be in superpositions of states. Quantum programmers are able to manipulate the superposition of qubits in order to solve problems that classical computing cannot do effectively, such as searching unsorted databases or integer factorization. IBM claims that the advent of quantum computing may progress the fields of medicine, logistics, financial services, artificial intelligence and cloud security.^[6]

Another active research topic is quantum teleportation, which deals with techniques to transmit quantum information over arbitrary distances.

While quantum mechanics primarily applies to the smaller atomic regimes of matter and energy, some systems exhibit quantum mechanical effects on a large scale. Superfluidity, the frictionless flow of a liquid at temperatures near absolute zero, is one well-known example. So is the closely related phenomenon of superconductivity, the frictionless flow of an electron gas in a conducting material (an electric current) at sufficiently low temperatures. The fractional quantum Hall effect is a topological ordered state which corresponds to patterns of long-range quantum entanglement.^[7] States with different topological orders (or different patterns of long range entanglements) cannot change into each other without a phase transition.

Quantum theory also provides accurate descriptions for many previously unexplained phenomena, such as black-body radiation and the stability of the orbitals of electrons in atoms. It has also given insight into the workings of many different biological systems, including smell receptors and protein structures.^[8] Recent work on photosynthesis has provided evidence that quantum correlations play an essential role in this fundamental process of plants and many other organisms.^[9] Even so, classical physics can often provide good approximations to results otherwise obtained by quantum physics, typically in circumstances with large numbers of particles or large quantum numbers. Since classical formulas are much simpler and easier to compute than quantum formulas, classical approximations are used and preferred when the system is large enough to render the effects of quantum mechanics insignificant.