Arithmetic rope
 From Wikipedia - Reading time: 6 min
From Wikipedia - Reading time: 6 min
This article may meet Wikipedia's criteria for speedy deletion as a copyright infringement(Copyvios report) of https://turba-delirantium.skyrocket.de/wissenschaft/rechenseil.htm (Copyvios report). This criterion applies only in unequivocal cases, where there is no free-content material on the page worth saving and no later edits requiring attribution – for more complicated situations, see Wikipedia:Copyright violations. See CSD G12.
If this article does not meet the criteria for speedy deletion, or you intend to fix it, please remove this notice, but do not remove this notice from pages that you have created yourself. If you created this page and you disagree with the given reason for deletion, you can click the button below and leave a message explaining why you believe it should not be deleted. You can also visit the talk page to check if you have received a response to your message. Note that this article may be deleted at any time if it unquestionably meets the speedy deletion criteria, or if an explanation posted to the talk page is found to be insufficient.
Note to administrators: this article has content on its talk page which should be checked before deletion. Note to administrators: If declining the request due to not meeting the criteria please consider whether there are still copyright problems with the page and if so, see these instructions for cleanup, or list it at Wikipedia:Copyright problems. Please be sure that the source of the alleged copyright violation is not itself a Wikipedia mirror. Also, ensure the submitter of this page has been notified about our copyright policy.Administrators: check links, talk, history (last), and logs before deletion. Consider checking Google. This page was last edited by 35.139.154.158 (contribs | logs) at 00:16, 9 January 2025 (UTC) (0 seconds ago) |
You can help expand this article with text translated from the corresponding article in French. Click [show] for important translation instructions.
|
This article relies largely or entirely on a single source. (January 2025) |

The arithmetic rope, knotted rope, thirteen-knot-rope, or thirteen-knot-cord, is an arithmetic tool made of rope which was widely used in the Middle Ages in Europe, where skilled professionals such as architects and shipbuilders used these ropes to solve various mathematical and geometrical problems.
An arithmetic rope generally has at least 13 knots[a] which are placed at equal intervals. Additional knots can be beneficial, especially for multiplication and division.[1]
In medieval architecture, the knotted rope was indispensable for architects, because it allowed the construction of equilateral and right triangles as well as circles.[1]
In the depiction of the liberal arts in Hortus deliciarum, the allegory of arithmetics is a female figure holding a knotted rope.[1]
Common applications
[edit]| Arithmetics[1] | |||
| Addition | X + Y = Z | X knots are counted, then another Y. The total number of counted knots is Z. | e.g.: 5 + 4 = 9
|
| Subtraction | X - Y = Z | X knots are counted, then Y knots are 'uncounted'. The total number of knots remaining counted is Z. | e.g.: 9 - 4 = 5
|
| Multiplication | X * Y = Z | X knots are counted, and the resulting distance is put together Y times. The total number of counted knots is Z. | e.g.: 4 * 3 = 12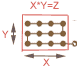
|
| Division | X / Y = Z (remainder Q) | X knots are counted. From these knots, Y knots are taken and grouped together until all are used up. The number of groups is Z; the number of remaining knots represents the remainder, Q. | e.g.: 12 / 4 = 3
|
| Geometrics[1] | |||
| Right angle | The two ends of the knotted rope are nailed together, and 5 knots are counted for the base. For the perpendicular side, 4 knots are required. The right-angled triangle is generated by pulling the sides taut. | ||
| Equilateral triangle | The two ends of the knotted rope are nailed together, and 5 knots are counted for each side. The sides are tautened to create an equilateral triangle. | 
| |
| Circle | One end is nailed down, and a stylus is attached at the desired distance. With the rope pulled taut, the stylus is moved around, forming a circle. | ||
See also
[edit]- Abacus
- Ad Quadratum: The Practical Application of Geometry in Medieval Architecture
- Knot theory
- Knotted cord
- Pythagorean theorem
- Quipu
- Rope stretcher
Notes
[edit]- ^ Hence the alternate name "13-knot-rope"
 KSF
KSF