Conceptual graph

Information mapping
Topics and fields
Business decision mapping Data visualization Graphic communication Infographics Information design Knowledge visualization Mental model Morphological analysis Ontology (information science) Schema (psychology) Visual analytics Visual language
Node–link approaches
Argument map Cladistics Cognitive map Concept lattice Concept map Conceptual graph Decision tree Dendrogram Graph drawing Hyperbolic tree Hypertext Issue map Issue tree Layered graph drawing Mind map Object-role modeling Organizational chart Pathfinder network Radial tree Semantic network Sociogram Timeline Topic map Tree structure ZigZag
See also
Design rationale Diagrammatic reasoning Entity–relationship model Geovisualization List of concept- and mind-mapping software Olog Ontology (philosophy) Problem structuring methods Semantic Web Treemapping Wicked problem
v t e

A conceptual graph (CG) is a formalism for knowledge representation. In the first published paper on CGs, John F. Sowa used them to represent the conceptual schemas used in database systems.^[1] The first book on CGs applied them to a wide range of topics in artificial intelligence, computer science, and cognitive science.^[2]

Since 1984, the model has been developed along three main directions: a graphical interface for first-order logic, a diagrammatic calculus of logics, and a graph-based knowledge representation and reasoning model.^[2]

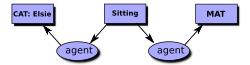
In this approach, a formula in first-order logic (predicate calculus) is represented by a labeled graph.

A linear notation, called the Conceptual Graph Interchange Format (CGIF), has been standardized in the ISO standard for common logic.

The diagram above is an example of the display form for a conceptual graph. Each box is called a concept node, and each oval is called a relation node. In CGIF, this CG would be represented by the following statement:

[Cat Elsie] [Sitting *x] [Mat *y] (agent ?x Elsie) (location ?x ?y)

In CGIF, brackets enclose the information inside the concept nodes, and parentheses enclose the information inside the relation nodes. The letters x and y, which are called coreference labels, show how the concept and relation nodes are connected. In CLIF, those letters are mapped to variables, as in the following statement:

(exists ((x Sitting) (y Mat)) (and (Cat Elsie) (agent x Elsie) (location x y)))

As this example shows, the asterisks on the coreference labels *x and *y in CGIF map to existentially quantified variables in CLIF, and the question marks on ?x and ?y map to bound variables in CLIF. A universal quantifier, represented @every*z in CGIF, would be represented forall (z) in CLIF.

Reasoning can be done by translating graphs into logical formulas, then applying a logical inference engine.

Another research branch continues the work on existential graphs of Charles Sanders Peirce, which were one of the origins of conceptual graphs as proposed by Sowa. In this approach, developed in particular by Dau (Dau 2003), conceptual graphs are conceptual diagrams rather than graphs in the sense of graph theory, and reasoning operations are performed by operations on these diagrams.

Key features of GBKR, the graph-based knowledge representation and reasoning model developed by Chein and Mugnier and the Montpellier group, can be summarized as follows:^[3]

• All kinds of knowledge (ontology, rules, constraints and facts) are labeled graphs, which provide an intuitive and easily understandable means to represent knowledge.
• Reasoning mechanisms are based on graph notions, basically the classical notion of graph homomorphism; this allows, in particular, to link basic reasoning problems to other fundamental problems in computer science (e.g., problems concerning conjunctive queries in relational databases, or constraint satisfaction problems).
• The formalism is logically founded, i.e., it has a semantics in first-order logic and the inference mechanisms are sound and complete with respect to deduction in first-order logic.
• From a computational viewpoint, the graph homomorphism notion was recognized in the 1990s as a central notion, and complexity results and efficient algorithms have been obtained in several domains.

COGITANT and COGUI are tools that implement the GBKR model. COGITANT is a library of C++ classes that implement most of the GBKR notions and reasoning mechanisms. COGUI is a graphical user interface dedicated to the construction of a GBKR knowledge base (it integrates COGITANT and, among numerous functionalities, it contains a translator from GBKR to RDF/S and conversely).

• Alphabet of human thought
• Chunking (psychology)
• Resource Description Framework (RDF)
• SPARQL (Graph Query Language)
• Semantic network

• Chein, Michel; Mugnier, Marie-Laure (2009). Graph-based Knowledge Representation: Computational Foundations of Conceptual Graphs. Springer. doi:10.1007/978-1-84800-286-9. ISBN 978-1-84800-285-2.
• Dau, F. (2003). The Logic System of Concept Graphs with Negation and Its Relationship to Predicate Logic. Lecture Notes in Computer Science. Vol. 2892. Springer.
• Sowa, John F. (July 1976). "Conceptual Graphs for a Data Base Interface" (PDF). IBM Journal of Research and Development. 20 (4): 336–357. doi:10.1147/rd.204.0336.
• Sowa, John F. (1984). Conceptual Structures: Information Processing in Mind and Machine. Reading, MA: Addison-Wesley. ISBN 978-0-201-14472-7.
• Velardi, Paola; Pazienza, Maria Teresa; De' Giovanetti, Mario (March 1988). "Conceptual graphs for the analysis and generation of sentences". IBM Journal of Research and Development. 32 (2). IBM Corp. Riverton, NJ, USA: 251–267. doi:10.1147/rd.322.0251.

• Conceptual Graphs Home Page
• Annual international conferences (ICCS) at DBLP
• Conceptual Graphs on John F. Sowa's Website