Coordinate descent
 From Wikipedia - Reading time: 9 min
From Wikipedia - Reading time: 9 min
Coordinate descent is an optimization algorithm that successively minimizes along coordinate directions to find the minimum of a function. At each iteration, the algorithm determines a coordinate or coordinate block via a coordinate selection rule, then exactly or inexactly minimizes over the corresponding coordinate hyperplane while fixing all other coordinates or coordinate blocks. A line search along the coordinate direction can be performed at the current iterate to determine the appropriate step size. Coordinate descent is applicable in both differentiable and derivative-free contexts.
Description
[edit]Coordinate descent is based on the idea that the minimization of a multivariable function can be achieved by minimizing it along one direction at a time, i.e., solving univariate (or at least much simpler) optimization problems in a loop.[1] In the simplest case of cyclic coordinate descent, one cyclically iterates through the directions, one at a time, minimizing the objective function with respect to each coordinate direction at a time. That is, starting with initial variable values
- ,
round defines from by iteratively solving the single variable optimization problems
for each variable of , for from 1 to .
Thus, one begins with an initial guess for a local minimum of , and gets a sequence iteratively.
By doing line search in each iteration, one automatically has
It can be shown that this sequence has similar convergence properties as steepest descent. No improvement after one cycle of line search along coordinate directions implies a stationary point is reached.
This process is illustrated below.
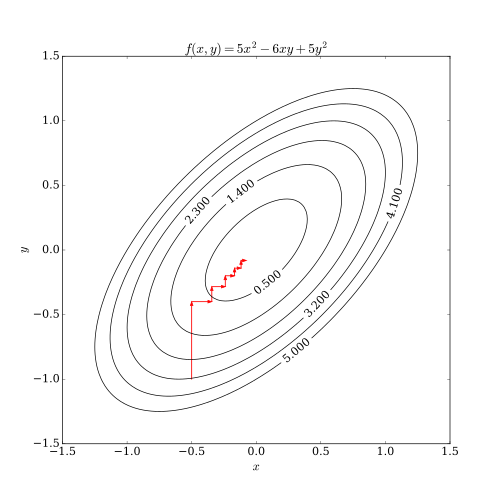
Differentiable case
[edit]In the case of a continuously differentiable function F, a coordinate descent algorithm can be sketched as:[1]
- Choose an initial parameter vector x.
- Until convergence is reached, or for some fixed number of iterations:
- Choose an index i from 1 to n.
- Choose a step size α.
- Update xi to xi − α∂F/∂xi(x).
The step size can be chosen in various ways, e.g., by solving for the exact minimizer of f(xi) = F(x) (i.e., F with all variables but xi fixed), or by traditional line search criteria.[1]
Limitations
[edit]Coordinate descent has two problems. One of them is the case of a non-smooth objective function. The following picture shows that coordinate descent iteration may get stuck at a non-stationary point if the level curves of the function are not smooth. Suppose that the algorithm is at the point (−2, −2); then there are two axis-aligned directions it can consider for taking a step, indicated by the red arrows. However, every step along these two directions will increase the objective function's value (assuming a minimization problem), so the algorithm will not take any step, even though both steps together would bring the algorithm closer to the optimum. While this example shows that coordinate descent does not necessarily converge to the optimum, it is possible to show formal convergence under reasonable conditions.[3]

The other problem is difficulty in parallelism. Since the nature of coordinate descent is to cycle through the directions and minimize the objective function with respect to each coordinate direction, coordinate descent is not an obvious candidate for massive parallelism. Recent research works have shown that massive parallelism is applicable to coordinate descent by relaxing the change of the objective function with respect to each coordinate direction.[4][5][6]
Applications
[edit]Coordinate descent algorithms are popular with practitioners owing to their simplicity, but the same property has led optimization researchers to largely ignore them in favor of more interesting (complicated) methods.[1] An early application of coordinate descent optimization was in the area of computed tomography[7] where it has been found to have rapid convergence[8] and was subsequently used for clinical multi-slice helical scan CT reconstruction.[9] A cyclic coordinate descent algorithm (CCD) has been applied in protein structure prediction.[10] Moreover, there has been increased interest in the use of coordinate descent with the advent of large-scale problems in machine learning, where coordinate descent has been shown competitive to other methods when applied to such problems as training linear support vector machines[11] (see LIBLINEAR) and non-negative matrix factorization.[12] They are attractive for problems where computing gradients is infeasible, perhaps because the data required to do so are distributed across computer networks.[13]
See also
[edit]- Adaptive coordinate descent – Improvement of the coordinate descent algorithm
- Conjugate gradient – Mathematical optimization algorithm
- Gradient descent – Optimization algorithm
- Line search – Optimization algorithm
- Mathematical optimization – Study of mathematical algorithms for optimization problems
- Newton's method – Method for finding stationary points of a function
- Stochastic gradient descent – Optimization algorithm – uses one example at a time, rather than one coordinate
References
[edit]- ^ a b c d Wright, Stephen J. (2015). "Coordinate descent algorithms". Mathematical Programming. 151 (1): 3–34. arXiv:1502.04759. doi:10.1007/s10107-015-0892-3. S2CID 15284973.
- ^ Gordon, Geoff; Tibshirani, Ryan (Fall 2012). "Coordinate descent" (PDF). Optimization 10-725 / 36-725. Carnegie Mellon University.
- ^ Spall, J. C. (2012). "Cyclic Seesaw Process for Optimization and Identification". Journal of Optimization Theory and Applications. 154 (1): 187–208. doi:10.1007/s10957-012-0001-1. S2CID 7795605.
- ^ Zheng, J.; Saquib, S. S.; Sauer, K.; Bouman, C. A. (2000-10-01). "Parallelizable Bayesian tomography algorithms with rapid, guaranteed convergence". IEEE Transactions on Image Processing. 9 (10): 1745–1759. Bibcode:2000ITIP....9.1745Z. CiteSeerX 10.1.1.34.4282. doi:10.1109/83.869186. ISSN 1057-7149. PMID 18262913.
- ^ Fessler, J. A.; Ficaro, E. P.; Clinthorne, N. H.; Lange, K. (1997-04-01). "Grouped-coordinate ascent algorithms for penalized-likelihood transmission image reconstruction". IEEE Transactions on Medical Imaging. 16 (2): 166–175. doi:10.1109/42.563662. hdl:2027.42/86021. ISSN 0278-0062. PMID 9101326. S2CID 1523517.
- ^ Wang, Xiao; Sabne, Amit; Kisner, Sherman; Raghunathan, Anand; Bouman, Charles; Midkiff, Samuel (2016-01-01). "High performance model based image reconstruction". Proceedings of the 21st ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming. PPoPP '16. New York, NY, USA: ACM. pp. 2:1–2:12. doi:10.1145/2851141.2851163. ISBN 9781450340922. S2CID 16569156.
- ^ Sauer, Ken; Bouman, Charles (February 1993). "A Local Update Strategy for Iterative Reconstruction from Projections" (PDF). IEEE Transactions on Signal Processing. 41 (2): 534–548. Bibcode:1993ITSP...41..534S. CiteSeerX 10.1.1.135.6045. doi:10.1109/78.193196.
- ^ Yu, Zhou; Thibault, Jean-Baptiste; Bouman, Charles; Sauer, Ken; Hsieh, Jiang (January 2011). "Fast Model-Based X-ray CT Reconstruction Using Spatially Non-Homogeneous ICD Optimization" (PDF). IEEE Transactions on Image Processing. 20 (1): 161–175. Bibcode:2011ITIP...20..161Y. doi:10.1109/TIP.2010.2058811. PMID 20643609. S2CID 9315957.
- ^ Thibault, Jean-Baptiste; Sauer, Ken; Bouman, Charles; Hsieh, Jiang (November 2007). "A Three-Dimensional Statistical Approach to Improved Image Quality for Multi-Slice Helical CT" (PDF). Medical Physics. 34 (11): 4526–4544. Bibcode:2007MedPh..34.4526T. doi:10.1118/1.2789499. PMID 18072519.
- ^ Canutescu, AA; Dunbrack, RL (2003). "Cyclic coordinate descent: A robotics algorithm for protein loop closure". Protein Science. 12 (5): 963–72. doi:10.1110/ps.0242703. PMC 2323867. PMID 12717019.
- ^ Hsieh, C. J.; Chang, K. W.; Lin, C. J.; Keerthi, S. S.; Sundararajan, S. (2008). "A dual coordinate descent method for large-scale linear SVM" (PDF). Proceedings of the 25th international conference on Machine learning - ICML '08. p. 408. doi:10.1145/1390156.1390208. ISBN 9781605582054. S2CID 7880266.
- ^ Hsieh, C. J.; Dhillon, I. S. (2011). Fast coordinate descent methods with variable selection for non-negative matrix factorization (PDF). Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining - KDD '11. p. 1064. doi:10.1145/2020408.2020577. ISBN 9781450308137.
- ^ Nesterov, Yurii (2012). "Efficiency of coordinate descent methods on huge-scale optimization problems" (PDF). SIAM J. Optim. 22 (2): 341–362. CiteSeerX 10.1.1.332.3336. doi:10.1137/100802001.
- Bezdek, J. C.; Hathaway, R. J.; Howard, R. E.; Wilson, C. A.; Windham, M. P. (1987), "Local convergence analysis of a grouped variable version of coordinate descent", Journal of Optimization Theory and Applications, vol. 54, no. 3, Kluwer Academic/Plenum Publishers, pp. 471–477, doi:10.1007/BF00940196, S2CID 120052975
- Bertsekas, Dimitri P. (1999). Nonlinear Programming, Second Edition Athena Scientific, Belmont, Massachusetts. ISBN 1-886529-00-0.
- Luo, Zhiquan; Tseng, P. (1992), "On the convergence of the coordinate descent method for convex differentiable minimization", Journal of Optimization Theory and Applications, vol. 72, no. 1, Kluwer Academic/Plenum Publishers, pp. 7–35, doi:10.1007/BF00939948, hdl:1721.1/3164, S2CID 121091844.
- Wu, TongTong; Lange, Kenneth (2008), "Coordinate descent algorithms for Lasso penalized regression", The Annals of Applied Statistics, vol. 2, no. 1, Institute of Mathematical Statistics, pp. 224–244, arXiv:0803.3876, doi:10.1214/07-AOAS147, S2CID 16350311.
- Richtarik, Peter; Takac, Martin (April 2011), "Iteration complexity of randomized block-coordinate descent methods for minimizing a composite function", Mathematical Programming, vol. 144, no. 1–2, Springer, pp. 1–38, arXiv:1107.2848, doi:10.1007/s10107-012-0614-z, S2CID 16816638.
- Richtarik, Peter; Takac, Martin (December 2012), "Parallel coordinate descent methods for big data optimization", ArXiv:1212.0873, arXiv:1212.0873.
 KSF
KSF













