Covering relation
 From Wikipedia - Reading time: 6 min
From Wikipedia - Reading time: 6 min
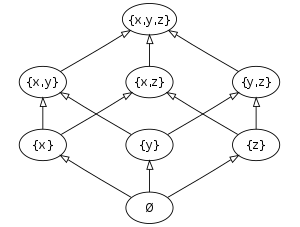
In mathematics, especially order theory, the covering relation of a partially ordered set is the binary relation which holds between comparable elements that are immediate neighbours. The covering relation is commonly used to graphically express the partial order by means of the Hasse diagram.
Definition
[edit]Let be a set with a partial order . As usual, let be the relation on such that if and only if and .
Let and be elements of .
Then covers , written , if and there is no element such that . Equivalently, covers if the interval is the two-element set .
When , it is said that is a cover of . Some authors also use the term cover to denote any such pair in the covering relation.
Examples
[edit]- In a finite linearly ordered set {1, 2, ..., n}, i + 1 covers i for all i between 1 and n − 1 (and there are no other covering relations).
- In the Boolean algebra of the power set of a set S, a subset B of S covers a subset A of S if and only if B is obtained from A by adding one element not in A.
- In Young's lattice, formed by the partitions of all nonnegative integers, a partition λ covers a partition μ if and only if the Young diagram of λ is obtained from the Young diagram of μ by adding an extra cell.
- The Hasse diagram depicting the covering relation of a Tamari lattice is the skeleton of an associahedron.
- The covering relation of any finite distributive lattice forms a median graph.
- On the real numbers with the usual total order ≤, the cover set is empty: no number covers another.
Properties
[edit]- If a partially ordered set is finite, its covering relation is the transitive reduction of the partial order relation. Such partially ordered sets are therefore completely described by their Hasse diagrams. On the other hand, in a dense order, such as the rational numbers with the standard order, no element covers another.
References
[edit]- Knuth, Donald E. (2006), The Art of Computer Programming, Volume 4, Fascicle 4, Addison-Wesley, ISBN 0-321-33570-8.
- Stanley, Richard P. (1997), Enumerative Combinatorics, vol. 1 (2nd ed.), Cambridge University Press, ISBN 0-521-55309-1.
- Brian A. Davey; Hilary Ann Priestley (2002), Introduction to Lattices and Order (2nd ed.), Cambridge University Press, ISBN 0-521-78451-4, LCCN 2001043910.
Licensed under CC BY-SA 3.0 | Source: https://en.wikipedia.org/wiki/Covering_relation22 views | ↧ Download as ZWI file
 KSF
KSF










![{\displaystyle [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663)

