Categories
  Encyclosphere.org ENCYCLOREADER
  supported by EncyclosphereKSF

Cubic crystal system

From Wikipedia - Reading time: 18 min
A rock containing three crystals of pyrite (FeS2). The crystal structure of pyrite is primitive cubic, and this is reflected in the cubic symmetry of its natural crystal facets.
A network model of a primitive cubic system
The primitive and cubic close-packed (also known as face-centered cubic) unit cells

In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals.

There are three main varieties of these crystals:

  • Primitive cubic (abbreviated cP and alternatively called simple cubic)
  • Body-centered cubic (abbreviated cI or bcc)
  • Face-centered cubic (abbreviated cF or fcc)

Note: the term fcc is often used in synonym for the cubic close-packed or ccp structure occurring in metals. However, fcc stands for a face-centered-cubic Bravais lattice, which is not necessarily close-packed when a motif is set onto the lattice points. E.g. the diamond and the zincblende lattices are fcc but not close-packed. Each is subdivided into other variants listed below. Although the unit cells in these crystals are conventionally taken to be cubes, the primitive unit cells often are not.

Bravais lattices

[edit]
Further information: Bravais lattice

The three Bravais latices in the cubic crystal system are:

Bravais lattice Primitive
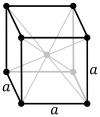
cubic 		Body-centered
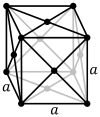
cubic 		Face-centered
cubic
Pearson symbol cP cI cF
Unit cell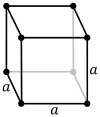

The primitive cubic lattice (cP) consists of one lattice point on each corner of the cube; this means each simple cubic unit cell has in total one lattice point. Each atom at a lattice point is then shared equally between eight adjacent cubes, and the unit cell therefore contains in total one atom (1⁄8 × 8).[1]

The body-centered cubic lattice (cI) has one lattice point in the center of the unit cell in addition to the eight corner points. It has a net total of two lattice points per unit cell (1⁄8 × 8 + 1).[1]

The face-centered cubic lattice (cF) has lattice points on the faces of the cube, that each gives exactly one half contribution, in addition to the corner lattice points, giving a total of four lattice points per unit cell (1⁄8 × 8 from the corners plus 1⁄2 × 6 from the faces).

The face-centered cubic lattice is closely related to the hexagonal close packed (hcp) system, where two systems differ only in the relative placements of their hexagonal layers. The [111] plane of a face-centered cubic lattice is a hexagonal grid.

Attempting to create a base-centered cubic lattice (i.e., putting an extra lattice point in the center of each horizontal face) results in a simple tetragonal Bravais lattice.

Coordination number (CN) is the number of nearest neighbors of a central atom in the structure.[1] Each sphere in a cP lattice has coordination number 6, in a cI lattice 8, and in a cF lattice 12.

Atomic packing factor (APF) is the fraction of volume that is occupied by atoms. The cP lattice has an APF of about 0.524, the cI lattice an APF of about 0.680, and the cF lattice an APF of about 0.740.

Crystal classes

[edit]
Further information: Crystallographic point group

The isometric crystal system class names, point groups (in Schönflies notation, Hermann–Mauguin notation, orbifold, and Coxeter notation), type, examples, international tables for crystallography space group number,[2] and space groups are listed in the table below. There are a total 36 cubic space groups.

No. Point group Type Example Space groups
Name[3] Schön. Intl Orb. Cox. Primitive Face-centered Body-centered
195–197 Tetartoidal T 23 332 [3,3]+ enantiomorphic Ullmannite, Sodium chlorate P23 F23 I23
198–199 P213 I213
200–204 Diploidal Th 2/m3
(m3) 		3*2 [3+,4] centrosymmetric Pyrite Pm3, Pn3 Fm3, Fd3 I3
205–206 Pa3 Ia3
207–211 Gyroidal O 432 432 [3,4]+ enantiomorphic Petzite P432, P4232 F432, F4132 I432
212–214 P4332, P4132 I4132
215–217 Hextetrahedral Td 43m *332 [3,3] Sphalerite P43m F43m I43m
218–220 P43n F43c I43d
221–230 Hexoctahedral Oh 4/m32/m
(m3m) 		*432 [3,4] centrosymmetric Galena, Halite Pm3m, Pn3n, Pm3n, Pn3m Fm3m, Fm3c, Fd3m, Fd3c Im3m, Ia3d

Other terms for hexoctahedral are: normal class, holohedral, ditesseral central class, galena type.

Single element structures

[edit]
Visualisation of a diamond cubic unit cell: 1. Components of a unit cell, 2. One unit cell, 3. A lattice of 3 x 3 x 3 unit cells
See also: Periodic table (crystal structure)

As a rule, since atoms in a solid attract each other, the more tightly packed arrangements of atoms tend to be more common. (Loosely packed arrangements do occur, though, for example if the orbital hybridization demands certain bond angles.) Accordingly, the primitive cubic structure, with especially low atomic packing factor, is rare in nature, but is found in polonium.[4][5] The bcc and fcc, with their higher densities, are both quite common in nature. Examples of bcc include iron, chromium, tungsten, and niobium. Examples of fcc include aluminium, copper, gold and silver.

Another important cubic crystal structure is the diamond cubic structure, which can appear in carbon, silicon, germanium, and tin. Unlike fcc and bcc, this structure is not a lattice, since it contains multiple atoms in its primitive cell. Other cubic elemental structures include the A15 structure found in tungsten, and the extremely complicated structure of manganese.

Multi-element structures

[edit]

Compounds that consist of more than one element (e.g. binary compounds) often have crystal structures based on the cubic crystal system. Some of the more common ones are listed here. These structures can be viewed as two or more interpenetrating sublattices where each sublattice occupies the interstitial sites of the others.

Caesium chloride structure

[edit]
See also: Category:Caesium chloride crystal structure
A caesium chloride unit cell. The two colors of spheres represent the two types of atoms.

One structure is the "interpenetrating primitive cubic" structure, also called a "caesium chloride" or B2 structure. This structure is often confused for a body-centered cubic structure because the arrangement of atoms is the same. However, the caesium chloride structure has a basis composed of two different atomic species. In a body-centered cubic structure, there would be translational symmetry along the [111] direction. In the caesium chloride structure, translation along the [111] direction results in a change of species. The structure can also be thought of as two separate simple cubic structures, one of each species, that are superimposed within each other. The corner of the chloride cube is the center of the caesium cube, and vice versa.[6]

This graphic shows the interlocking simple cubic lattices of cesium and chlorine. You can see them separately and as they are interlocked in what looks like a body-centered cubic arrangement

It works the same way for the NaCl structure described in the next section.  If you take out the Cl atoms, the leftover Na atoms still form an FCC structure, not a simple cubic structure.

In the unit cell of CsCl, each ion is at the center of a cube of ions of the opposite kind, so the coordination number is eight. The central cation is coordinated to 8 anions on the corners of a cube as shown, and similarly, the central anion is coordinated to 8 cations on the corners of a cube. Alternately, one could view this lattice as a simple cubic structure with a secondary atom in its cubic void.

In addition to caesium chloride itself, the structure also appears in certain other alkali halides when prepared at low temperatures or high pressures.[7] Generally, this structure is more likely to be formed from two elements whose ions are of roughly the same size (for example, ionic radius of Cs+ = 167 pm, and Cl− = 181 pm).

The space group of the caesium chloride (CsCl) structure is called Pm3m (in Hermann–Mauguin notation), or "221" (in the International Tables for Crystallography). The Strukturbericht designation is "B2".[8]

There are nearly a hundred rare earth intermetallic compounds that crystallize in the CsCl structure, including many binary compounds of rare earths with magnesium,[9] and with elements in groups 11, 12,[10][11] and 13. Other compounds showing caesium chloride like structure are CsBr, CsI, high-temperature RbCl, AlCo, AgZn, BeCu, MgCe, RuAl and SrTl.[citation needed]

Rock-salt structure

[edit]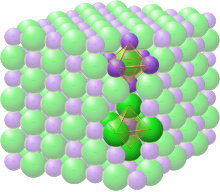
See also: Category:Rock salt crystal structure
The rock-salt crystal structure. Each atom has six nearest neighbours, with octahedral geometry.

The space group of the rock-salt or halite (sodium chloride) structure is denoted as Fm3m (in Hermann–Mauguin notation), or "225" (in the International Tables for Crystallography). The Strukturbericht designation is "B1".[12]

In the rock-salt structure, each of the two atom types forms a separate face-centered cubic lattice, with the two lattices interpenetrating so as to form a 3D checkerboard pattern. The rock-salt structure has octahedral coordination: Each atom's nearest neighbors consist of six atoms of the opposite type, positioned like the six vertices of a regular octahedron. In sodium chloride there is a 1:1 ratio of sodium to chlorine atoms.  The structure can also be described as an FCC lattice of sodium with chlorine occupying each octahedral void or vice versa.[6]

Examples of compounds with this structure include sodium chloride itself, along with almost all other alkali halides, and "many divalent metal oxides, sulfides, selenides, and tellurides".[7] According to the radius ratio rule, this structure is more likely to be formed if the cation is somewhat smaller than the anion (a cation/anion radius ratio of 0.414 to 0.732).

The interatomic distance (distance between cation and anion, or half the unit cell length a) in some rock-salt-structure crystals are: 2.3 Å (2.3 × 10−10 m) for NaF,[13] 2.8 Å for NaCl,[14] and 3.2 Å for SnTe.[15] Most of the alkali metal hydrides and halides have the rock salt structure, though a few have the caesium chloride structure instead.

Alkali metal hydrides and halides with the rock salt structure
Hydrides Fluorides Chlorides Bromides Iodides
Lithium Lithium hydride Lithium fluoride[16] Lithium chloride Lithium bromide Lithium iodide
Sodium Sodium hydride Sodium fluoride[16] Sodium chloride Sodium bromide Sodium iodide
Potassium Potassium hydride Potassium fluoride[16] Potassium chloride Potassium bromide Potassium iodide
Rubidium Rubidium hydride Rubidium fluoride Rubidium chloride Rubidium bromide Rubidium iodide
Caesium Caesium hydride Caesium fluoride (CsCl structure)
Alkaline earth metal chalcogenides with the rock salt structure
Oxides Sulfides Selenides Tellurides Polonides
Magnesium Magnesium oxide Magnesium sulfide Magnesium selenide[17] Magnesium telluride[18] (NiAs structure)
Calcium Calcium oxide Calcium sulfide Calcium selenide[19] Calcium telluride Calcium polonide[20]
Strontium Strontium oxide Strontium sulfide Strontium selenide Strontium telluride Strontium polonide[20]
Barium Barium oxide Barium sulfide Barium selenide Barium telluride Barium polonide[20]
Rare-earth[21] and actinoid pnictides with the rock salt structure
Nitrides Phosphides Arsenides Antimonides Bismuthides
Scandium Scandium nitride Scandium phosphide Scandium arsenide[22] Scandium antimonide[23] Scandium bismuthide[24]
Yttrium Yttrium nitride Yttrium phosphide Yttrium arsenide[25] Yttrium antimonide Yttrium bismuthide[26]
Lanthanum Lanthanum nitride[27] Lanthanum phosphide[28] Lanthanum arsenide[25] Lanthanum antimonide Lanthanum bismuthide[29]
Cerium Cerium nitride[27] Cerium phosphide[28] Cerium arsenide[25] Cerium antimonide Cerium bismuthide[29]
Praseodymium Praseodymium nitride[27] Praseodymium phosphide[28] Praseodymium arsenide[25] Praseodymium antimonide[30] Praseodymium bismuthide[29]
Neodymium Neodymium nitride[27] Neodymium phosphide[28] Neodymium arsenide[25] Neodymium antimonide[30] Neodymium bismuthide[29]
Promethium ? ? ? ? ?
Samarium Samarium nitride[27] Samarium phosphide[28] Samarium arsenide[25] Samarium antimonide[30] Samarium bismuthide[29]
Europium Europium nitride[27] Europium phosphide (Na2O2 structure)[31] (unstable)[32]
Gadolinium Gadolinium nitride[27] Gadolinium phosphide Gadolinium arsenide[25] Gadolinium antimonide[30] Gadolinium bismuthide[29]
Terbium Terbium nitride[27] Terbium phosphide Terbium arsenide[25] Terbium antimonide[30] Terbium bismuthide[29]
Dysprosium Dysprosium nitride[27] Dysprosium phosphide Dysprosium arsenide Dysprosium antimonide Dysprosium bismuthide[29]
Holmium Holmium nitride[27] Holmium phosphide Holmium arsenide[25] Holmium antimonide Holmium bismuthide[29]
Erbium Erbium nitride[27] Erbium phosphide Erbium arsenide[25] Erbium antimonide Erbium bismuthide[29]
Thulium Thulium nitride[27] Thulium phosphide Thulium arsenide Thulium antimonide Thulium bismuthide[29]
Ytterbium Ytterbium nitride[27] Ytterbium phosphide Ytterbium arsenide[25] Ytterbium antimonide (unstable)[33][34]
Lutetium Lutetium nitride[27] Lutetium phosphide Lutetium arsenide Lutetium antimonide Lutetium bismuthide
Actinium ? ? ? ? ?
Thorium Thorium nitride[35] Thorium phosphide[35] Thorium arsenide[35] Thorium antimonide[35] (CsCl structure)
Protactinium ? ? ? ? ?
Uranium Uranium nitride[35] Uranium monophosphide[35] Uranium arsenide[35] Uranium antimonide[35] Uranium bismuthide[36]
Neptunium Neptunium nitride Neptunium phosphide Neptunium arsenide Neptunium antimonide Neptunium bismuthide[36]
Plutonium Plutonium nitride[35] Plutonium phosphide[35] Plutonium arsenide[35] Plutonium antimonide[35] Plutonium bismuthide[36]
Americium Americium nitride[36] Americium phosphide[36] Americium arsenide[36] Americium antimonide[36] Americium bismuthide[36]
Curium Curium nitride[37] Curium phosphide[37] Curium arsenide[37] Curium antimonide[37] Curium bismuthide[37]
Berkelium Berkelium nitride[37] Berkelium phosphide[37] Berkelium arsenide[37] ? Berkelium bismuthide[37]
Californium ? ? Californium arsenide[37] ? Californium bismuthide[37]
Rare-earth and actinoid chalcogenides with the rock salt structure
Oxides Sulfides Selenides Tellurides Polonides
Scandium (unstable)[38] Scandium monosulfide
Yttrium Yttrium monosulfide[39]
Lanthanum Lanthanum monosulfide[40]
Cerium Cerium monosulfide[40] Cerium monoselenide[41] Cerium monotelluride[41]
Praseodymium Praseodymium monosulfide[40] Praseodymium monoselenide[41] Praseodymium monotelluride[41]
Neodymium Neodymium monosulfide[40] Neodymium monoselenide[41] Neodymium monotelluride[41]
Promethium ? ? ? ?
Samarium Samarium monosulfide[40] Samarium monoselenide Samarium monotelluride Samarium monopolonide[42]
Europium Europium monoxide Europium monosulfide[40] Europium monoselenide[43] Europium monotelluride[43] Europium monopolonide[42]
Gadolinium (unstable)[38] Gadolinium monosulfide[40]
Terbium Terbium monosulfide[40] Terbium monopolonide[42]
Dysprosium Dysprosium monosulfide[40] Dysprosium monopolonide[42]
Holmium Holmium monosulfide[40] Holmium monopolonide[42]
Erbium Erbium monosulfide[40]
Thulium Thulium monosulfide[40] Thulium monopolonide[42]
Ytterbium Ytterbium monoxide Ytterbium monosulfide[40] Ytterbium monopolonide[42]
Lutetium (unstable)[38][44] Lutetium monosulfide[40] Lutetium monopolonide[42]
Actinium ? ? ? ?
Thorium Thorium monosulfide[35] Thorium monoselenide[35] (CsCl structure)[45]
Protactinium ? ? ? ?
Uranium Uranium monosulfide[35] Uranium monoselenide[35] Uranium monotelluride[35]
Neptunium Neptunium monosulfide Neptunium monoselenide Neptunium monotelluride
Plutonium Plutonium monosulfide[35] Plutonium monoselenide[35] Plutonium monotelluride[35]
Americium Americium monosulfide[36] Americium monoselenide[36] Americium monotelluride[36]
Curium Curium monosulfide[37] Curium monoselenide[37] Curium monotelluride[37]
Transition metal carbides and nitrides with the rock salt structure
Carbides Nitrides
Titanium Titanium carbide Titanium nitride
Zirconium Zirconium carbide Zirconium nitride
Hafnium Hafnium carbide Hafnium nitride[46]
Vanadium Vanadium carbide Vanadium nitride
Niobium Niobium carbide Niobium nitride
Tantalum Tantalum carbide (CoSn structure)
Chromium (unstable)[47] Chromium nitride

Many transition metal monoxides also have the rock salt structure (TiO, VO, CrO, MnO, FeO, CoO, NiO, CdO). The early actinoid monocarbides also have this structure (ThC, PaC, UC, NpC, PuC).[37]

Fluorite structure

[edit]
Main article: Fluorite structure
See also: Category:Fluorite crystal structure

Much like the rock salt structure, the fluorite structure (AB2) is also an Fm3m structure but has 1:2 ratio of ions. The anti-fluorite structure is nearly identical, except the positions of the anions and cations are switched in the structure. They are designated Wyckoff positions 4a and 8c whereas the rock-salt structure positions are 4a and 4b.[48][49]

Zincblende structure

[edit]
See also: Category:Zincblende crystal structure
A zincblende unit cell

The space group of the Zincblende structure is called F43m (in Hermann–Mauguin notation), or 216.[50][51] The Strukturbericht designation is "B3".[52]

The Zincblende structure (also written "zinc blende") is named after the mineral zincblende (sphalerite), one form of zinc sulfide (β-ZnS). As in the rock-salt structure, the two atom types form two interpenetrating face-centered cubic lattices. However, it differs from rock-salt structure in how the two lattices are positioned relative to one another. The zincblende structure has tetrahedral coordination: Each atom's nearest neighbors consist of four atoms of the opposite type, positioned like the four vertices of a regular tetrahedron. In zinc sulfide the ratio of zinc to sulfur is 1:1.[6] Altogether, the arrangement of atoms in zincblende structure is the same as diamond cubic structure, but with alternating types of atoms at the different lattice sites. The structure can also be described as an FCC lattice of zinc with sulfur atoms occupying half of the tetrahedral voids or vice versa.[6]

Examples of compounds with this structure include zincblende itself, lead(II) nitrate, many compound semiconductors (such as gallium arsenide and cadmium telluride), and a wide array of other binary compounds.[citation needed] The boron group pnictogenides usually have a zincblende structure, though the nitrides are more common in the wurtzite structure, and their zincblende forms are less well known polymorphs.[53][54]

Copper halides with the zincblende structure
Fluorides Chlorides Bromides Iodides
Copper Copper(I) fluoride Copper(I) chloride Copper(I) bromide Copper(I) iodide
Beryllium and Group 12 chalcogenides with the zincblende structure
Sulfides Selenides Tellurides Polonides
Beryllium Beryllium sulfide Beryllium selenide Beryllium telluride Beryllium polonide[55][56]
Zinc Zinc sulfide Zinc selenide Zinc telluride Zinc polonide
Cadmium Cadmium sulfide Cadmium selenide Cadmium telluride Cadmium polonide
Mercury Mercury sulfide Mercury selenide Mercury telluride –

This group is also known as the II-VI family of compounds, most of which can be made in both the zincblende (cubic) or wurtzite (hexagonal) form.

Group 13 pnictogenides with the zincblende structure
Nitrides Phosphides Arsenides Antimonides
Boron Boron nitride* Boron phosphide Boron arsenide Boron antimonide
Aluminium Aluminium nitride* Aluminium phosphide Aluminium arsenide Aluminium antimonide
Gallium Gallium nitride* Gallium phosphide Gallium arsenide Gallium antimonide
Indium Indium nitride* Indium phosphide Indium arsenide Indium antimonide

This group is also known as the III-V family of compounds.

The structure of the Heusler compounds with formula X2YZ (e. g., Co2MnSi).

Heusler structure

[edit]
Main article: Heusler compound

The Heusler structure, based on the structure of Cu2MnAl, is a common structure for ternary compounds involving transition metals. It has the space group Fm3m (No. 225), and the Strukturbericht designation is L21. Together with the closely related half-Heusler and inverse-Huesler compounds, there are hundreds of examples.

Iron monosilicide structure

[edit]
See also: Category:Iron monosilicide structure type
Diagram of the iron monosilicide structure.

The space group of the iron monosilicide structure is P213 (No. 198), and the Strukturbericht designation is B20. This is a chiral structure, and is sometimes associated with helimagnetic properties. There are four atoms of each element for a total of eight atoms in the unit cell.

Examples occur among the transition metal silicides and germanides, as well as a few other compounds such as gallium palladide.

Transition metal silicides and germanides with the FeSi structure
Silicides Germanides
Manganese Manganese monosilicide Manganese germanide
Iron Iron monosilicide Iron germanide
Cobalt Cobalt monosilicide Cobalt germanide
Chromium Chromium(IV) silicide Chromium(IV) germanide

Weaire–Phelan structure

[edit]
Weaire–Phelan structure

A Weaire–Phelan structure has Pm3n (223) symmetry.

It has three orientations of stacked tetradecahedrons with pyritohedral cells in the gaps. It is found as a crystal structure in chemistry where it is usually known as a "type I clathrate structure". Gas hydrates formed by methane, propane, and carbon dioxide at low temperatures have a structure in which water molecules lie at the nodes of the Weaire–Phelan structure and are hydrogen bonded together, and the larger gas molecules are trapped in the polyhedral cages.

See also

[edit]

References

[edit]
  1. ^ a b c De Wolff, P. M.; Belov, N. V.; Bertaut, E. F.; Buerger, M. J.; Donnay, J. D. H.; Fischer, W.; Hahn, Th.; Koptsik, V. A.; MacKay, A. L.; Wondratschek, H.; Wilson, A. J. C.; Abrahams, S. C. (1985). "Nomenclature for crystal families, Bravais-lattice types and arithmetic classes. Report of the International Union of Crystallography Ad-Hoc Committee on the Nomenclature of Symmetry". Acta Crystallographica Section A. 41 (3): 278. doi:10.1107/S0108767385000587.
  2. ^ Prince, E., ed. (2006). International Tables for Crystallography. doi:10.1107/97809553602060000001. ISBN 978-1-4020-4969-9. S2CID 146060934.
  3. ^ Crystallography and Minerals Arranged by Crystal Form, Webmineral
  4. ^ Greenwood, Norman N.; Earnshaw, Alan (1997). Chemistry of the Elements (2nd ed.). Butterworth-Heinemann. ISBN 978-0-08-037941-8.
  5. ^ The original discovery was in J. Chem. Phys. 14, 569 (1946).
  6. ^ a b c d "Cubic Lattices and Close Packing". 3 October 2013. Archived from the original on 2020-11-01.
  7. ^ a b Seitz, Modern Theory of Solids (1940), p.49
  8. ^ The CsCl (B2) Structure Archived 2008-09-15 at the Wayback Machine
  9. ^ Saccone, A.; Delfino, S.; Macció, D.; Ferro, R. (1993). "Magnesium-rare earth phase diagrams: Experimental investigation of the Ho-Mg system". Journal of Phase Equilibria. 14 (3): 280–287. doi:10.1007/bf02668225. S2CID 95011597.
  10. ^ Kanematu, K; T. Alfieri, G.; Banks, E. (1969). "Magnetic Studies of Rare Earth Zinc Compounds with CsCl Structure". Journal of the Physical Society of Japan. 26 (2): 244–248. Bibcode:1969JPSJ...26..244K. doi:10.1143/jpsj.26.244.
  11. ^ Buschow, K. H. J. (1974). "Magnetic properties of CsCl‐type rare‐earth cadmium compounds". The Journal of Chemical Physics. 61 (11): 4666–4670. Bibcode:1974JChPh..61.4666B. doi:10.1063/1.1681788.
  12. ^ The NaCl (B1) Structure Archived 2008-10-19 at the Wayback Machine
  13. ^ Sundquist, J. J.; Lin, C. C. (1981). "Electronic structure of the F centre in a sodium fluoride crystal". Journal of Physics C: Solid State Physics. 14 (32): 4797–4805. Bibcode:1981JPhC...14.4797S. doi:10.1088/0022-3719/14/32/016.
  14. ^ Abrahams, S. C.; Bernstein, J. L. (1965). "Accuracy of an automatic diffractometer. Measurement of the sodium chloride structure factors". Acta Crystallogr. 18 (5): 926–932. doi:10.1107/S0365110X65002244.
  15. ^ Kao, W.; Peretti, E. (1970). "The ternary subsystem Sn4As3-SnAs-SnTe". Journal of the Less Common Metals. 22: 39–50. doi:10.1016/0022-5088(70)90174-8.
  16. ^ a b c J. Aigueperse, P. Mollard, D. Devilliers, M. Chemla, R. Faron, R. Romano, J. P. Cuer, "Fluorine Compounds, Inorganic" (section 4) in Ullmann’s Encyclopedia of Industrial Chemistry, Wiley-VCH, Weinheim, 2005. doi:10.1002/14356007.a11_307.
  17. ^ Broch, Einar (1927-06-01). "Präzisionsbestimmungen der Gitterkonstanten der Verbindungen MgO, MgS, MgSe, MnO und MnSe". Zeitschrift für Physikalische Chemie (in German). 127U (1): 446–454. doi:10.1515/zpch-1927-12724. S2CID 100227546.
  18. ^ Mir, Showkat H.; Jha, Prakash C.; Dabhi, Shweta; Jha, Prafulla K. (2016). "Ab initio study of phase stability, lattice dynamics and thermodynamic properties of magnesium chalcogenides". Materials Chemistry and Physics. 175: 54–61. doi:10.1016/j.matchemphys.2016.02.066.
  19. ^ Louail, L.; Haddadi, K.; Maouche, D.; Ali Sahraoui, F.; Hachemi, A. (2008). "Electronic band structure of calcium selenide under pressure". Physica B: Condensed Matter. 403 (18): 3022–3026. Bibcode:2008PhyB..403.3022L. doi:10.1016/j.physb.2008.03.009.
  20. ^ a b c Brown, S.A.; Brown, P.L. (2019). The Aqueous Chemistry of Polonium and the Practical Application of its Thermochemistry. Elsevier Science. p. 25. ISBN 978-0-12-819309-9.
  21. ^ Hulliger, F. (1979). "Chapter 33 Rare earth pnictides". Handbook on the Physics and Chemistry of Rare Earths. Vol. 4. Elsevier. pp. 153–236. doi:10.1016/s0168-1273(79)04006-x. ISBN 9780444852168.
  22. ^ Gschneidner, K. A.; Calderwood, F. W. (1986). "The As−Sc (Arsenic-Scandium) system". Bulletin of Alloy Phase Diagrams. 7 (4): 348–349. doi:10.1007/bf02873011.
  23. ^ Hayashi, J; Shirotani, I; Hirano, K; Ishimatsu, N; Shimomura, O; Kikegawa, T (2003). "Structural phase transition of ScSb and YSb with a NaCl-type structure at high pressures". Solid State Communications. 125 (10): 543–546. Bibcode:2003SSCom.125..543H. doi:10.1016/s0038-1098(02)00889-x.
  24. ^ Horovitz, C.T. (2012). Scandium Its Occurrence, Chemistry Physics, Metallurgy, Biology and Technology. Elsevier Science. p. 273. ISBN 978-0-323-14451-3.
  25. ^ a b c d e f g h i j k Ono, S.; Despault, J.G.; Calvert, L.D.; Taylor, J.B. (1970). "Rare-earth arsenides". Journal of the Less Common Metals. 22 (1): 51–59. doi:10.1016/0022-5088(70)90175-x.
  26. ^ Schmidt, F.A.; McMasters, O.D.; Lichtenberg, R.R. (1969). "The yttrium-bismuth alloy system". Journal of the Less Common Metals. 18 (3): 215–220. doi:10.1016/0022-5088(69)90159-3.
  27. ^ a b c d e f g h i j k l m n Natali, F.; Ruck, B.J.; Plank, N.O.V.; Trodahl, H.J.; Granville, S.; Meyer, C.; Lambrecht, W.R.L. (2013). "Rare-earth mononitrides". Progress in Materials Science. 58 (8): 1316–1360. arXiv:1208.2410. doi:10.1016/j.pmatsci.2013.06.002. S2CID 118566136.
  28. ^ a b c d e Ono, S.; Nomura, K.; Hayakawa, H. (1974). "Syntheses of new rare-earth phosphides". Journal of the Less Common Metals. 38 (2–3): 119–130. doi:10.1016/0022-5088(74)90055-1.
  29. ^ a b c d e f g h i j k Yoshihara, K.; Taylor, J.B.; Calvert, L.D.; Despault, J.G. (1975). "Rare-earth bismuthides". Journal of the Less Common Metals. 41 (2): 329–337. doi:10.1016/0022-5088(75)90038-7.
  30. ^ a b c d e Hayashi, J.; Shirotani, I.; Tanaka, Y.; Adachi, T.; Shimomura, O.; Kikegawa, T. (2000). "Phase transitions of LnSb (Ln=lanthanide) with NaCl-type structure at high pressures". Solid State Communications. 114 (11): 561–565. Bibcode:2000SSCom.114..561H. doi:10.1016/s0038-1098(00)00113-7.
  31. ^ Gschneidner, K. A.; Calderwood, F. W. (1986). "The As−Eu (Arsenic-Europium) system". Bulletin of Alloy Phase Diagrams. 7 (3): 279–283. doi:10.1007/bf02869009.
  32. ^ Taylor, J. B.; Calvert, L. D.; Wang, Y. (1979). "Powder data for some new europium antimonides and bismuthides". Journal of Applied Crystallography. 12 (2): 249–251. doi:10.1107/s0021889879012309.
  33. ^ Okamoto, H. (1999). "Bi-Yb (bismuth-ytterbium)". Journal of Phase Equilibria. 20 (4): 453. doi:10.1361/105497199770335640.
  34. ^ Duan, Xu; Wu, Fan; Chen, Jia; Zhang, Peiran; Liu, Yang; Yuan, Huiqiu; Cao, Chao (2018). "Tunable electronic structure and topological properties of LnPn (Ln=Ce, Pr, Sm, Gd, Yb; Pn=Sb, Bi)". Communications Physics. 1 (1): 71. arXiv:1802.04554. Bibcode:2018CmPhy...1...71D. doi:10.1038/s42005-018-0074-8.
  35. ^ a b c d e f g h i j k l m n o p q r s t Kruger, O.L.; Moser, J.B. (1967). "Lattice constants and melting points of actinide-group IVA-VIA compounds with NaCl-type structures". Journal of Physics and Chemistry of Solids. 28 (11): 2321–2325. Bibcode:1967JPCS...28.2321K. doi:10.1016/0022-3697(67)90257-0.
  36. ^ a b c d e f g h i j k Vogt, O.; Mattenberger, K. (1995). "The magnetism of localized or nearly localized 4f and 5f shells". Journal of Alloys and Compounds. 223 (2): 226–236. doi:10.1016/0925-8388(94)09005-x.
  37. ^ a b c d e f g h i j k l m n o Benedict, U.; Holzapfel, W.B. (1993). "Chapter 113 High-pressure studies — Structural aspects". Lanthanides/Actinides: Physics I. Handbook on the Physics and Chemistry of Rare Earths. Vol. 17. Elsevier. pp. 245–300. doi:10.1016/s0168-1273(05)80030-3. ISBN 9780444815026.
  38. ^ a b c Leger, J.M.; Yacoubi, N.; Loriers, J. (1981). "Synthesis of rare earth monoxides". Journal of Solid State Chemistry. 36 (3): 261–270. Bibcode:1981JSSCh..36..261L. doi:10.1016/0022-4596(81)90436-9.
  39. ^ Roedhammer, P.; Reichardt, W.; Holtzberg, F. (1978). "Soft-Mode Behavior in the Phonon Dispersion of YS". Physical Review Letters. 40 (7): 465–468. Bibcode:1978PhRvL..40..465R. doi:10.1103/physrevlett.40.465.
  40. ^ a b c d e f g h i j k l m n Didchenko, R.; Gortsema, F.P. (1963). "Some electric and magnetic properties of rare earth monosulfides and nitrides". Journal of Physics and Chemistry of Solids. 24 (7): 863–870. Bibcode:1963JPCS...24..863D. doi:10.1016/0022-3697(63)90062-3.
  41. ^ a b c d e f Smolensky, G. A.; Adamjan, V. E.; Loginov, G. M. (1968). "Antiferromagnetic Properties of Light Rare Earth Monochalcogenides". Journal of Applied Physics. 39 (2): 786–790. Bibcode:1968JAP....39..786S. doi:10.1063/1.2163619.
  42. ^ a b c d e f g h Kershner, C.J.; DeSando, R.J.; Heidelberg, R.F.; Steinmeyer, R.H. (1966). "Rare earth polonides". Journal of Inorganic and Nuclear Chemistry. 28 (8): 1581–1588. doi:10.1016/0022-1902(66)80054-4.
  43. ^ a b Wachter, P. (1972). "The optical electrical and magnetic properties of the europium chalcogenides and the rare earth pnictides". C R C Critical Reviews in Solid State Sciences. 3 (2): 189–241. doi:10.1080/10408437208244865.
  44. ^ Meyer, G (1991). Synthesis of Lanthanide and Actinide Compounds. Dordrecht: Springer Netherlands. p. 237. ISBN 978-94-011-3758-4. OCLC 840310000.
  45. ^ D'Eye, R. W. M.; Sellman, P. G. (1954). "The thorium–tellurium system". J. Chem. Soc.: 3760–3766. doi:10.1039/jr9540003760.
  46. ^ Friedrich, Alexandra; Winkler, Björn; Juarez-Arellano, Erick A.; Bayarjargal, Lkhamsuren (2011). "Synthesis of Binary Transition Metal Nitrides, Carbides and Borides from the Elements in the Laser-Heated Diamond Anvil Cell and Their Structure-Property Relations". Materials. 4 (10): 1648–1692. Bibcode:2011Mate....4.1648F. doi:10.3390/ma4101648. PMC 5448873. PMID 28824101.
  47. ^ Venkatraman, M.; Neumann, J. P. (1990). "The C-Cr (Carbon-Chromium) System". Bulletin of Alloy Phase Diagrams. 11 (2): 152–159. doi:10.1007/bf02841701.
  48. ^ "Fluorite". aflow.org. Retrieved 2020-05-22.
  49. ^ "Rock Salt". aflow.org. Retrieved 2020-05-22.
  50. ^ Kantorovich, L. (2004). Quantum Theory of the Solid State. Springer. p. 32. ISBN 1-4020-2153-4.
  51. ^ Birkbeck College, University of London
  52. ^ The Zincblende (B3) Structure. Naval Research Laboratory, U.S. Archived October 19, 2008, at the Wayback Machine
  53. ^ Wang, L.D.; Kwok, H.S. (2000). "Cubic aluminum nitride and gallium nitride thin films prepared by pulsed laser deposition". Applied Surface Science. 154–155 (1–4): 439–443. Bibcode:2000ApSS..154..439W. doi:10.1016/s0169-4332(99)00372-4.
  54. ^ Oseki, Masaaki; Okubo, Kana; Kobayashi, Atsushi; Ohta, Jitsuo; Fujioka, Hiroshi (2014). "Field-effect transistors based on cubic indium nitride". Scientific Reports. 4 (1): 3951. Bibcode:2014NatSR...4E3951O. doi:10.1038/srep03951. PMC 3912472. PMID 24492240.
  55. ^ Greenwood, Norman N.; Earnshaw, Alan (1984). Chemistry of the Elements. Oxford: Pergamon Press. p. 899. ISBN 978-0-08-022057-4..
  56. ^ Moyer, Harvey V. (1956). "Chemical Properties of Polonium". In Moyer, Harvey V. (ed.). Polonium (Report). Oak Ridge, Tenn.: United States Atomic Energy Commission. pp. 33–96. doi:10.2172/4367751. TID-5221..

Further reading

[edit]
  • Hurlbut, Cornelius S.; Klein, Cornelis, 1985, Manual of Mineralogy, 20th ed., Wiley, ISBN 0-471-80580-7
[edit]
Licensed under CC BY-SA 3.0 | Source: https://en.wikipedia.org/wiki/Cubic_crystal_system
3 views |
↧ Download as ZWI file
Encyclosphere.org EncycloReader is supported by the EncyclosphereKSF