Geographical distance
 From Wikipedia - Reading time: 17 min
From Wikipedia - Reading time: 17 min
| Geodesy |
|---|
 |

Geographical distance or geodetic distance is the distance measured along the surface of the Earth, or the shortest arch length.
The formulae in this article calculate distances between points which are defined by geographical coordinates in terms of latitude and longitude. This distance is an element in solving the second (inverse) geodetic problem.
Introduction
[edit]Calculating the distance between geographical coordinates is based on some level of abstraction; it does not provide an exact distance, which is unattainable if one attempted to account for every irregularity in the surface of the Earth.[1] Common abstractions for the surface between two geographic points are:
- Flat surface;
- Spherical surface;
- Ellipsoidal surface.
All abstractions above ignore changes in elevation. Calculation of distances which account for changes in elevation relative to the idealized surface are not discussed in this article.
Classification of Formulae based on Approximation
[edit]- Tunnel-distance based approximations: Flat surface, Gauss-mid-latitude;
- 0-th-order approximation: Spherical surface;
- higher-order approximations based on Ellipsoid: : Andoyer(1932); Andoyer-Lambert(1942), : Andoyer-Lambert-Thomas(1970), : Vincenty(1975), : Kaney(2011); on the hemisphere
The theoretical estimations of error are added in above and is the flattening of the Earth.
Nomenclature
[edit]Arc distance, is the minimum distance along the surface of sphere/ellipsoid calculated between two points, and . Whereas, the tunnel distance, or chord length, , is measured along Cartesian straight line. The geographical coordinates of the two points, as (latitude, longitude) pairs, are and respectively. Which of the two points is designated as is not important for the calculation of distance.
Latitude and longitude coordinates on maps are usually expressed in degrees. In the given forms of the formulae below, one or more values must be expressed in the specified units to obtain the correct result. Where geographic coordinates are used as the argument of a trigonometric function, the values may be expressed in any angular units compatible with the method used to determine the value of the trigonometric function. Many electronic calculators allow calculations of trigonometric functions in either degrees or radians. The calculator mode must be compatible with the units used for geometric coordinates.
Differences in latitude and longitude are labeled and calculated as follows:
It is not important whether the result is positive or negative when used in the formulae below.
"Mean latitude" is labeled and calculated as follows:
Unless specified otherwise, the radius of the Earth for the calculations below is:
- = 6,371.009 kilometers = 3,958.761 statute miles = 3,440.069 nautical miles.
= Distance between the two points, as measured along the surface of the Earth and in the same units as the value used for radius unless specified otherwise.
Singularities and discontinuity of latitude/longitude
[edit]The approximation of sinusoidal functions of , appearing in some flat-surface formulae below, may induce singularity and discontinuity. It may also degrade the accuracy in the case of higher latitude.
Longitude has singularities at the Poles (longitude is undefined) and a discontinuity at the ±180° meridian. Also, planar projections of the circles of constant latitude are highly curved near the Poles. Hence, the above equations for delta latitude/longitude (, ) and mean latitude () may not give the expected answer for positions near the Poles or the ±180° meridian. Consider e.g. the value of ("east displacement") when and are on either side of the ±180° meridian, or the value of ("mean latitude") for the two positions (=89°, =45°) and (=89°, =−135°).
If a calculation based on latitude/longitude should be valid for all Earth positions, it should be verified that the discontinuity and the Poles are handled correctly. Another solution is to use n-vector instead of latitude/longitude, since this representation does not have discontinuities or singularities.
Flat-surface approximation formulae for very short distance
[edit]A planar approximation for the surface of the Earth may be useful over very small distances. It approximates the arc length, , to the tunnel distance, , or omits the conversion between arc and chord lengths shown below.
The shortest distance between two points in plane is a Cartesian straight line. The Pythagorean theorem is used to calculate the distance between points in a plane.
Even over short distances, the accuracy of geographic distance calculations which assume a flat Earth depend on the method by which the latitude and longitude coordinates have been projected onto the plane. The projection of latitude and longitude coordinates onto a plane is the realm of cartography.
The formulae presented in this section provide varying degrees of accuracy.
Spherical Earth approximation formulae
[edit]This formula takes into account the variation in distance between meridians with latitude:
The square root appearing above can be eliminated for such application as ordering locations by distance in a database query.
In the case of medium or low latitude
[edit]The above is furthermore simplified by approximating sinusoidal functions of , justified except for high latitude:
- .
Ellipsoidal Earth approximation formulae
[edit]The above formula is extended for ellipsoidal Earth:
- ,
where and are the meridional and its perpendicular, or "normal", radii of curvature of Earth (See also "Geographic coordinate conversion" for their formulas).
It is derived by the approximation of in the square root.
In the case of medium or low latitude
[edit]The above is furthermore simplified by approximating sinusoidal functions of , justified except for high latitude as above:[2][3]
FCC's formula
[edit]The FCC prescribes the following formulae for distances not exceeding 475 kilometres (295 mi):[4]
- where
- = Distance in kilometers;
- and are in degrees;
- must be in units compatible with the method used for determining
- Where and are in units of kilometers per arc degree. They are derived from radii of curvature of Earth as follows:
- = kilometers per arc degree of latitude difference;
- = kilometers per arc degree of longitude difference;
- Note that the expressions in the FCC formula are derived from the truncation of the binomial series expansion form of and , set to the Clarke 1866 reference ellipsoid. For a more computationally efficient implementation of the formula above, multiple applications of cosine can be replaced with a single application and use of recurrence relation for Chebyshev polynomials.
Polar coordinate flat-Earth formula
[edit]
- where the colatitude values are in radians:
- For a latitude measured in degrees, the colatitude in radians may be calculated as follows:
Spherical-surface formulae
[edit]If one is willing to accept a possible error of 0.5%, one can use formulas of spherical trigonometry on the sphere that best approximates the surface of the Earth.
The shortest distance along the surface of a sphere between two points on the surface is along the great-circle which contains the two points.
The great-circle distance article gives the formula for calculating the shortest arch length on a sphere about the size of the Earth. That article includes an example of the calculation. For example, from tunnel distance ,
For short distances (),
Tunnel distance
[edit]A tunnel between points on Earth is defined by a Cartesian line through three-dimensional space between the points of interest. The tunnel distance is the great-circle chord length and may be calculated as follows for the corresponding unit sphere:
Ellipsoidal-surface formulae
[edit]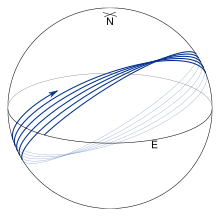
An ellipsoid approximates the surface of the Earth much better than a sphere or a flat surface does. The shortest distance along the surface of an ellipsoid between two points on the surface is along the geodesic. Geodesics follow more complicated paths than great circles and in particular, they usually don't return to their starting positions after one circuit of the Earth. This is illustrated in the figure on the right where f is taken to be 1/50 to accentuate the effect. Finding the geodesic between two points on the Earth, the so-called inverse geodetic problem, was the focus of many mathematicians and geodesists over the course of the 18th and 19th centuries with major contributions by Clairaut,[5] Legendre,[6] Bessel,[7] and Helmert English translation of Astron. Nachr. 4, 241–254 (1825). Errata.[8] Rapp[9] provides a good summary of this work.
Methods for computing the geodesic distance are widely available in geographical information systems, software libraries, standalone utilities, and online tools. The most widely used algorithm is by Vincenty,[10] who uses a series which is accurate to third order in the flattening of the ellipsoid, i.e., about 0.5 mm; however, the algorithm fails to converge for points that are nearly antipodal. (For details, see Vincenty's formulae.) This defect is cured in the algorithm given by Karney,[11] who employs series which are accurate to sixth order in the flattening. This results in an algorithm which is accurate to full double precision and which converges for arbitrary pairs of points on the Earth. This algorithm is implemented in GeographicLib.[12]
The exact methods above are feasible when carrying out calculations on a computer. They are intended to give millimeter accuracy on lines of any length; one can use simpler formulas if one doesn't need millimeter accuracy, or if one does need millimeter accuracy but the line is short.
The short-line methods have been studied by several researchers. Rapp,[13] Chap. 6, describes the Puissant method, the Gauss mid-latitude method, and the Bowring method.[14] Karl Hubeny[15] got the expanded series of Gauss mid-latitude one represented as the correction to flat-surface one.
Lambert's formula for long lines
[edit]Historically, the long-line formulae were derived in the form of expansion series with regard to flattening .[16][17]
Lambert's formulae[18] use the first-order correction and reduced latitude, , for better accuracy. They give accuracy on the order of 10 meters over thousands of kilometers.
First convert the latitudes , of the two points to reduced latitudes , . Then calculate the central angle in radians between two points and on a sphere using the Great-circle distance method (haversine formula), with longitudes and being the same on the sphere as on the spheroid.
- ,
where is the equatorial radius of the chosen spheroid.
On the GRS 80 spheroid Lambert's formula is off by
- 0 North 0 West to 40 North 120 West, 12.6 meters
- 0N 0W to 40N 60W, 6.6 meters
- 40N 0W to 40N 60W, 0.85 meter
Gauss mid-latitude method for short lines
[edit]It has the similar form of the arc length converted from tunnel distance. Detailed formulas are given by Rapp,[13] §6.4. It is consistent with the above-mentioned flat-surface formulae apparently.
Bowring's method for short lines
[edit]Bowring maps the points to a sphere of radius R′, with latitude and longitude represented as φ′ and λ′. Define
where the second eccentricity squared is
The spherical radius is
(The Gaussian curvature of the ellipsoid at φ1 is 1/R′2.) The spherical coordinates are given by
where , , , . The resulting problem on the sphere may be solved using the techniques for great-circle navigation to give approximations for the spheroidal distance and bearing. Detailed formulas are given by Rapp[13] §6.5, Bowring,[14] and Karney.[19]
Altitude correction
[edit]The variation in altitude from the topographical or ground level down to the sphere's or ellipsoid's surface, also changes the scale of distance measurements.[20] The slant distance s (chord length) between two points can be reduced to the arc length on the ellipsoid surface S as:[21]
where R is evaluated from Earth's azimuthal radius of curvature and h are ellipsoidal heights are each point. The first term on the right-hand side of the equation accounts for the mean elevation and the second term for the inclination. A further reduction of the above Earth normal section length to the ellipsoidal geodesic length is often negligible.[21]
See also
[edit]- Arc measurement
- Earth radius
- Spherical Earth
- Great-circle distance
- Great-circle navigation
- Ground sample distance
- Vincenty's formulae
- Meridian arc
- Scale (map)
References
[edit]- ^ "The British Cartographic Society > How long is the UK coastline?". Archived from the original on 2012-05-22. Retrieved 2008-12-06.
- ^ Williams, E. (2013). "Aviation Formulary". Retrieved 2024-06-23.
- ^ Williams, E. (2002). "Navigation on the spheroidal earth". Retrieved 2023-11-28.
- ^ "Reference points and distance computations" (PDF). Code of Federal Regulations (Annual Edition). Title 47: Telecommunication. 73 (208). October 1, 2016. Retrieved 8 November 2017.
- ^ Clairaut, A. C. (1735). "Détermination géometrique de la perpendiculaire à la méridienne tracée par M. Cassini" [Geometrical determination of the perpendicular to the meridian drawn by Jacques Cassini]. Mémoires de l'Académie Royale des Sciences de Paris 1733 (in French): 406–416.
- ^ Legendre, A. M. (1806). "Analyse des triangles tracées sur la surface d'un sphéroïde" [Analysis of spheroidal triangles]. Mémoires de l'Institut National de France (in French) (1st semester): 130–161.
- ^
Bessel, F. W. (2010) [1825]. "The calculation of longitude and latitude from geodesic measurements". Astronomische Nachrichten. 331 (8). . Translated by C. F. F. Karney & R. E. Deakin: 852–861. arXiv:0908.1824. Bibcode:2010AN....331..852K. doi:10.1002/asna.201011352. S2CID 118760590.
{{cite journal}}: CS1 maint: postscript (link) - ^
Helmert, F. R. (1964) [1880]. Mathematical and Physical Theories of Higher Geodesy. Vol. 1. St. Louis: Aeronautical Chart and Information Center.
{{cite book}}: CS1 maint: postscript (link) English translation of Die Mathematischen und Physikalischen Theorieen der Höheren Geodäsie, Vol. 1 (Teubner, Leipzig, 1880). - ^ Rapp, R. H. (March 1993). Geometric Geodesy, Part II (Technical report). Ohio State University. Retrieved 2011-08-01.
- ^
Vincenty, T. (April 1975). "Direct and Inverse Solutions of Geodesics on the Ellipsoid with application of nested equations" (PDF). Survey Review. 23 (176): 88–93. doi:10.1179/sre.1975.23.176.88. Retrieved 2009-07-11. Addendum: Survey Review 23 (180): 294 (1976).
{{cite journal}}: CS1 maint: postscript (link) - ^ Karney, C. F. F. (2013). "Algorithms for geodesics". Journal of Geodesy. 87 (1): 43–55. arXiv:1109.4448. Bibcode:2013JGeod..87...43K. doi:10.1007/s00190-012-0578-z. S2CID 119310141. – (open access). Addenda.
- ^ Karney, C. F. F. (2013). "GeographicLib". 1.32.
- ^ a b c
Rapp, R, H (1991). Geometric Geodesy, Part I (Report). Ohio Start Univ. hdl:1811/24333.
{{cite report}}: CS1 maint: multiple names: authors list (link) - ^ a b Bowring, B. R. (1981). "The direct and inverse problems for short geodesic lines on the ellipsoid". Surveying and Mapping. 41 (2): 135–141.
- ^ Hubeny, K. (1954). Entwicklung der Gauss'schen Mittelbreitenformeln, Österreichische Zeitschrift für Vermessungswesen.
- ^ Forsyth, A. R. (1927). Calculus of Variations. Cambridge Univ. Press. ISBN 978-1-107-64083-2. OCLC 250050479..
- ^ Henri Andoyer: Formule donnant la longueur de la géodésique joignant 2 points de l’ellipsoïde donnés par leurs coordonnées géographiques, Bulletin Géodésique, Volume 34, Number 1, April 1932, pages 77–81, https://doi.org/10.1007%2FBF03030136
- ^ Lambert, W. D (1942). "The distance between two widely separated points on the surface of the earth". J. Washington Academy of Sciences. 32 (5): 125–130.
- ^ "GeographicLib: Geodesics on an ellipsoid of revolution". geographiclib.sourceforge.io. Retrieved 2024-08-04.
- ^ "Archived copy" (PDF). Archived from the original (PDF) on 2014-08-27. Retrieved 2014-08-26.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ a b Torge & Müller (2012) Geodesy, De Gruyter, p.249
External links
[edit]- An online geodesic calculator (based on GeographicLib).
- An online geodesic bibliography.
 KSF
KSF









































































![{\displaystyle {\begin{aligned}\tan \phi _{1}'&={\frac {\tan \phi _{1}}{B}},\\\Delta \phi '&={\frac {\Delta \phi }{B}}{\biggl [}1+{\frac {3e'^{2}}{4B^{2}}}(\Delta \phi )\sin(2\phi _{1}+{\tfrac {2}{3}}\Delta \phi ){\biggr ]},\\\Delta \lambda '&=A\Delta \lambda ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acee78ead1818a6414b8442884ef1fc4f387b8cf)




