Superconducting quantum computing

Superconducting quantum computing is a branch of solid state physics and quantum computing that implements superconducting electronic circuits using superconducting qubits as artificial atoms, or quantum dots. For superconducting qubits, the two logic states are the ground state and the excited state, denoted ${\displaystyle |g\rangle {\text{ and }}|e\rangle }$respectively.^[1] Research in superconducting quantum computing is conducted by companies such as Google,^[2] IBM,^[3] IMEC,^[4] BBN Technologies,^[5] Rigetti,^[6] and Intel.^[7] Many recently developed QPUs (quantum processing units, or quantum chips) use superconducting architecture.

As of May 2016^[update], up to 9 fully controllable qubits are demonstrated in the 1D array,^[8] and up to 16 in 2D architecture.^[3] In October 2019, the Martinis group, partnered with Google, published an article demonstrating novel quantum supremacy, using a chip composed of 53 superconducting qubits.^[9]

Classical computation models rely on physical implementations consistent with the laws of classical mechanics.^[10] Classical descriptions are accurate only for specific systems consisting of a relatively large number of atoms. A more general description of nature is given by quantum mechanics. Quantum computation studies quantum phenomena applications beyond the scope of classical approximation, with the purpose of performing quantum information processing and communication. Various models of quantum computation exist, but the most popular models incorporate concepts of qubits and quantum gates (or gate-based superconducting quantum computing).

Superconductors are implemented due to the fact that at low temperatures they have infinite conductivity and zero resistance. Each qubit is built using semiconductor circuits with an LC circuit: a capacitor and an inductor.^{[citation needed]}

Superconducting capacitors and inductors are used to produce a resonant circuit that dissipates almost no energy, as heat can disrupt quantum information. The superconducting resonant circuits are a class of artificial atoms that can be used as qubits. Theoretical and physical implementations of quantum circuits are widely different. Implementing a quantum circuit had its own set of challenges and must abide by DiVincenzo's criteria, conditions proposed by theoretical physicist David P DiVincenzo,^[11] which is set of criteria for the physical implementation of superconducting quantum computing, where the initial five criteria ensure that the quantum computer is in line with the postulates of quantum mechanics and the remaining two pertaining to the relaying of this information over a network.^{[citation needed]}

We map the ground and excited states of these atoms to the 0 and 1 state as these are discrete and distinct energy values and therefore it is in line with the postulates of quantum mechanics. In such a construction however an electron can jump to multiple other energy states and not be confined to our excited state; therefore, it is imperative that the system be limited to be affected only by photons with energy difference required to jump from the ground state to the excited state.^[12] However, this leaves one major issue, we require uneven spacing between our energy levels to prevent photons with the same energy from causing transitions between neighboring pairs of states. Josephson junctions are superconducting elements with a nonlinear inductance, which is critically important for qubit implementation.^[12] The use of this nonlinear element in the resonant superconducting circuit produces uneven spacings between the energy levels.^{[citation needed]}

A qubit is a generalization of a bit (a system with two possible states) capable of occupying a quantum superposition of both states. A quantum gate, on the other hand, is a generalization of a logic gate describing the transformation of one or more qubits once a gate is applied given their initial state. Physical implementation of qubits and gates is challenging for the same reason that quantum phenomena are difficult to observe in everyday life given the minute scale on which they occur. One approach to achieving quantum computers is by implementing superconductors whereby quantum effects are macroscopically observable, though at the price of extremely low operation temperatures.

Unlike typical conductors, superconductors possess a critical temperature at which resistivity plummets to nearly zero and conductivity is drastically increased. In superconductors, the basic charge carriers are pairs of electrons (known as Cooper pairs), rather than single fermions as found in typical conductors.^[13] Cooper pairs are loosely bound and have an energy state lower than that of Fermi Energy. Electrons forming Cooper pairs possess equal and opposite momentum and spin so that the total spin of the Cooper pair is an integer spin. Hence, Cooper pairs are bosons. Two such superconductors which have been used in superconducting qubit models are niobium and tantalum, both d-band superconductors.^[14]

Once cooled to nearly absolute zero, a collection of bosons collapse into their lowest energy quantum state (the ground state) to form a state of matter known as Bose–Einstein condensate. Unlike fermions, bosons may occupy the same quantum energy level (or quantum state) and do not obey the Pauli exclusion principle. Classically, Bose-Einstein Condensate can be conceptualized as multiple particles occupying the same position in space and having equal momentum. Because interactive forces between bosons are minimized, Bose-Einstein Condensates effectively act as a superconductor. Thus, superconductors are implemented in quantum computing because they possess both near infinite conductivity and near zero resistance. The advantages of a superconductor over a typical conductor, then, are twofold in that superconductors can, in theory, transmit signals nearly instantaneously and run infinitely with no energy loss. The prospect of actualizing superconducting quantum computers becomes all the more promising considering NASA's recent development of the Cold Atom Lab in outer space where Bose-Einstein Condensates are more readily achieved and sustained (without rapid dissipation) for longer periods of time without the constraints of gravity.^[15]

At each point of a superconducting electronic circuit (a network of electrical elements), the condensate wave function describing charge flow is well-defined by some complex probability amplitude. In typical conductor electrical circuits, this same description is true for individual charge carriers except that the various wave functions are averaged in macroscopic analysis, making it impossible to observe quantum effects. The condensate wave function becomes useful in allowing design and measurement of macroscopic quantum effects. Similar to the discrete atomic energy levels in the Bohr model, only discrete numbers of magnetic flux quanta can penetrate a superconducting loop. In both cases, quantization results from complex amplitude continuity. Differing from microscopic implementations of quantum computers (such as atoms or photons), parameters of superconducting circuits are designed by setting (classical) values to the electrical elements composing them such as by adjusting capacitance or inductance.

To obtain a quantum mechanical description of an electrical circuit, a few steps are required. Firstly, all electrical elements must be described by the condensate wave function amplitude and phase rather than by closely related macroscopic current and voltage descriptions used for classical circuits. For instance, the square of the wave function amplitude at any arbitrary point in space corresponds to the probability of finding a charge carrier there. Therefore, the squared amplitude corresponds to a classical charge distribution. The second requirement to obtain a quantum mechanical description of an electrical circuit is that generalized Kirchhoff's circuit laws are applied at every node of the circuit network to obtain the system's equations of motion. Finally, these equations of motion must be reformulated to Lagrangian mechanics such that a quantum Hamiltonian is derived describing the total energy of the system.

Superconducting quantum computing devices are typically designed in the radio-frequency spectrum, cooled in dilution refrigerators below 15 mK and addressed with conventional electronic instruments, e.g. frequency synthesizers and spectrum analyzers. Typical dimensions fall on the range of micrometers, with sub-micrometer resolution, allowing for the convenient design of a Hamiltonian system with well-established integrated circuit technology. Manufacturing superconducting qubits follows a process involving lithography, depositing of metal, etching, and controlled oxidation as described in.^[16] Manufacturers continue to improve the lifetime of superconducting qubits and have made significant improvements since the early 2000s.^[16]: 4

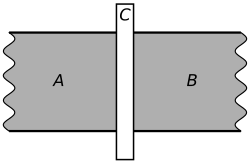
One distinguishable attribute of superconducting quantum circuits is the use of Josephson junctions. Josephson junctions are an electrical element which does not exist in normal conductors. Recall that a junction is a weak connection between two leads of wire (in this case a superconductive wire) on either side of a thin layer of insulator material only a few atoms thick, usually implemented using shadow evaporation technique. The resulting Josephson junction device exhibits the Josephson Effect whereby the junction produces a supercurrent. An image of a single Josephson junction is shown to the right. The condensate wave function on the two sides of the junction are weakly correlated, meaning that they are allowed to have different superconducting phases. This distinction of nonlinearity contrasts continuous superconducting wire for which the wave function across the junction must be continuous. Current flow through the junction occurs by quantum tunneling, seeming to instantaneously "tunnel" from one side of the junction to the other. This tunneling phenomenon is unique to quantum systems. Thus, quantum tunneling is used to create nonlinear inductance, essential for qubit design as it allows a design of anharmonic oscillators for which energy levels are discretized (or quantized) with nonuniform spacing between energy levels, denoted ${\displaystyle \Delta E}$.^[1] In contrast, the quantum harmonic oscillator cannot be used as a qubit as there is no way to address only two of its states, given that the spacing between every energy level and the next is exactly the same.

The three primary superconducting qubit archetypes are the phase, charge and flux qubit. Many hybridizations of these archetypes exist including the fluxonium,^[17] transmon,^[18] Xmon,^[19] and quantronium.^[20] For any qubit implementation the logical quantum states ${\displaystyle \{|0\rangle ,|1\rangle \}}$ are mapped to different states of the physical system (typically to discrete energy levels or their quantum superpositions). Each of the three archetypes possess a distinct range of Josephson energy to charging energy ratio. Josephson energy refers to the energy stored in Josephson junctions when current passes through, and charging energy is the energy required for one Cooper pair to charge the junction's total capacitance.^[21] Josephson energy can be written as

${\displaystyle U_{j}=-{\frac {I_{0}\Phi _{0}}{2\pi }}\cos \delta }$,

where ${\displaystyle I_{0}}$ is the critical current parameter of the Josephson junction, ${\displaystyle \textstyle \Phi _{0}={\frac {h}{2e}}}$ is (superconducting) flux quantum, and ${\displaystyle \delta }$ is the phase difference across the junction.^[21] Notice that the term ${\displaystyle cos\delta }$ indicates nonlinearity of the Josephson junction.^[21] Charge energy is written as

${\displaystyle E_{C}={\frac {e^{2}}{2C}}}$,

where ${\displaystyle C}$ is the junction's capacitance and ${\displaystyle e}$ is electron charge.^[21] Of the three archetypes, phase qubits allow the most of Cooper pairs to tunnel through the junction, followed by flux qubits, and charge qubits allow the fewest.

The phase qubit possesses a Josephson to charge energy ratio on the order of magnitude ${\displaystyle 10^{6}}$. For phase qubits, energy levels correspond to different quantum charge oscillation amplitudes across a Josephson junction, where charge and phase are analogous to momentum and position respectively as analogous to a quantum harmonic oscillator. Note that in this context phase is the complex argument of the superconducting wave function (also known as the superconducting order parameter), not the phase between the different states of the qubit.

The flux qubit (also known as a persistent-current qubit) possesses a Josephson to charging energy ratio on the order of magnitude ${\displaystyle 10}$. For flux qubits, the energy levels correspond to different integer numbers of magnetic flux quanta trapped in a superconducting ring.

Fluxonium qubits are a specific type of flux qubit whose Josephson junction is shunted by a linear inductor of ${\displaystyle E_{J}\gg E_{L}}$ where ${\displaystyle E_{L}=(\hbar /2e)^{2}/L}$.^[24] In practice, the linear inductor is usually implemented by a Josephson junction array that is composed of a large number (can be often ${\displaystyle N>100}$) of large-sized Josephson junctions connected in a series. Under this condition, the Hamiltonian of a fluxonium can be written as:

${\displaystyle {\hat {H}}=4E_{C}{\hat {n}}^{2}+{\frac {1}{2}}E_{L}({\hat {\phi }}-\phi _{\mathrm {ext} })^{2}-E_{J}\cos {\hat {\phi }}}$.

One important property of the fluxonium qubit is the longer qubit lifetime at the half flux sweet spot, which can exceed 1 millisecond.^[24][25] Another crucial advantage of the fluxonium qubit biased at the sweet spot is the large anharmonicity, which allows fast local microwave control and mitigates spectral crowding problems, leading to better scalability.^[26][27]

The charge qubit, also known as the Cooper pair box, possesses a Josephson to charging energy ratio on the order of magnitude ${\displaystyle <1}$. For charge qubits, different energy levels correspond to an integer number of Cooper pairs on a superconducting island (a small superconducting area with a controllable number of charge carriers).^[28] Indeed, the first experimentally realized qubit was the Cooper pair box, achieved in 1999.^[29]

Transmons are a special type of qubit with a shunted capacitor specifically designed to mitigate noise. The transmon qubit model was based on the Cooper pair box^[31] (illustrated in the table above in row one column one). It was also the first qubit to demonstrate quantum supremacy.^[32] The increased ratio of Josephson to charge energy mitigates noise. Two transmons can be coupled using a coupling capacitor.^[1] For this 2-qubit system the Hamiltonian is written

${\displaystyle {\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})}$,

where ${\displaystyle J}$ is current density and ${\displaystyle \sigma }$ is surface charge density.^[1]

The Xmon is very similar in design to a transmon in that it originated based on the planar transmon model.^[33] An Xmon is essentially a tunable transmon. The major distinguishing difference between transmon and Xmon qubits is the Xmon qubits is grounded with one of its capacitor pads.^[34]

Another variation of the transmon qubit is the Gatemon. Like the Xmon, the Gatemon is a tunable variation of the transmon. The Gatemon is tunable via gate voltage.

In 2022 researchers from IQM Quantum Computers, Aalto University, and VTT Technical Research Centre of Finland discovered a novel superconducting qubit known as the Unimon.^[36] A relatively simple qubit, the Unimon consists of a single Josephson junction shunted by a linear inductor (possessing an inductance not depending on current) inside a (superconducting) resonator.^[37] Unimons have increased anharmocity and display faster operation time resulting in lower susceptibility to noise errors.^[37] In addition to increased anharmocity, other advantages Unimon qubit include decreased susceptibility to flux noise and complete insensitivity to dc charge noise.^[22]

Superconducting Qubit Archetypes ^[38]

Type Aspect	Charge qubit	RF-SQUID qubit (prototype of the Flux Qubit)	Phase qubit
Circuit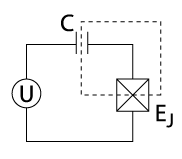
Hamiltonian	${\displaystyle H=E_{C}(N-N_{g})^{2}-E_{J}\cos \phi }$ In this case ${\displaystyle N}$ is the number of Cooper pairs to tunnel through the junction, ${\displaystyle N_{g}=CV_{0}/2e}$ is the charge on the capacitor in units of Cooper pairs number, ${\displaystyle E_{C}=(2e)^{2}/2(C_{J}+C)}$ is the charging energy associated with both capacitance ${\displaystyle C}$ and Josephson junction capacitance ${\displaystyle C_{J}}$.	${\displaystyle H={\frac {q^{2}}{2C_{J}}}+\left({\frac {\Phi _{0}}{2\pi }}\right)^{2}{\frac {\phi ^{2}}{2L}}-E_{J}\cos \left[\phi -\Phi {\frac {2\pi }{\Phi _{0}}}\right]}$ Note that ${\displaystyle \phi }$ is only allowed to take values greater than ${\displaystyle 2\pi }$ and is alternatively defined as the time integral of voltage along inductance ${\displaystyle L}$.	${\displaystyle H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi }$Here ${\displaystyle \Phi _{0}}$ is magnetic flux quantum.
Potential

In the table above, the three superconducting qubit archetypes are reviewed. In the first row, the qubit's electrical circuit diagram is presented. The second row depicts a quantum Hamiltonian derived from the circuit. Generally, the Hamiltonian is the sum of the system's kinetic and potential energy components (analogous to a particle in a potential well). For the Hamiltonians denoted, ${\displaystyle \phi }$ is the superconducting wave function phase difference across the junction, ${\displaystyle C_{J}}$ is the capacitance associated with the Josephson junction, and ${\displaystyle q}$ is the charge on the junction capacitance. For each potential depicted, only solid wave functions are used for computation. The qubit potential is indicated by a thick red line, and schematic wave function solutions are depicted by thin lines, lifted to their appropriate energy level for clarity.

Note that particle mass corresponds to an inverse function of the circuit capacitance and that the shape of the potential is governed by regular inductors and Josephson junctions. Schematic wave solutions in the third row of the table show the complex amplitude of the phase variable. Specifically, if a qubit's phase is measured while the qubit occupies a particular state, there is a non-zero probability of measuring a specific value only where the depicted wave function oscillates. All three rows are essentially different presentations of the same physical system.

The GHz energy gap between energy levels of a superconducting qubit is designed to be compatible with available electronic equipment, due to the terahertz gap (lack of equipment in the higher frequency band). The superconductor energy gap implies a top limit of operation below ~1THz beyond which Cooper pairs break, so energy level separation cannot be too high. On the other hand, energy level separation cannot be too small due to cooling considerations: a temperature of 1 K implies energy fluctuations of 20 GHz. Temperatures of tens of millikelvins are achieved in dilution refrigerators and allow qubit operation at a ~5 GHz energy level separation. Qubit energy level separation is frequently adjusted by controlling a dedicated bias current line, providing a "knob" to fine tune the qubit parameters.

A single qubit gate is achieved by rotation in the Bloch sphere. Rotations between different energy levels of a single qubit are induced by microwave pulses sent to an antenna or transmission line coupled to the qubit with a frequency resonant with the energy separation between levels. Individual qubits may be addressed by a dedicated transmission line or by a shared one if the other qubits are off resonance. The axis of rotation is set by quadrature amplitude modulation of microwave pulse, while pulse length determines the angle of rotation.^[39]

More formally (following the notation of ^[39]) for a driving signal

${\displaystyle {\mathcal {E}}(t)={\mathcal {E}}^{x}(t)\cos(\omega _{d}t)+{\mathcal {E}}^{y}(t)\sin(\omega _{d}t)}$

of frequency ${\displaystyle \omega _{d}}$, a driven qubit Hamiltonian in a rotating wave approximation is

${\displaystyle H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}}$,

where ${\displaystyle \omega }$ is the qubit resonance and ${\displaystyle \sigma _{x},\sigma _{y}}$ are Pauli matrices.

To implement a rotation about the ${\displaystyle X}$ axis, one can set ${\displaystyle {\mathcal {E}}^{y}(t)=0}$ and apply a microwave pulse at frequency ${\displaystyle \omega _{d}=\omega }$ for time ${\displaystyle t_{g}}$. The resulting transformation is

${\displaystyle U_{x}=\exp \left\{-{\frac {i}{\hbar }}\int _{0}^{t_{g}}H^{R}dt\right\}=\exp \left\{-i\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt\cdot \sigma _{x}/2\right\}}$.

This is exactly the rotation operator ${\displaystyle R_{X}(\theta )}$ by angle ${\displaystyle \theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt}$ about the ${\displaystyle X}$ axis in the Bloch sphere. A rotation about the ${\displaystyle Y}$ axis can be implemented in a similar way. Showing the two rotation operators is sufficient for satisfying universality as every single qubit unitary operator ${\displaystyle U}$ may be presented as ${\displaystyle U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})}$ (up to a global phase which is physically inconsequential) by a procedure known as the ${\displaystyle X-Y}$ decomposition.^[40] Setting ${\displaystyle \int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt=\pi }$ results in the transformation

${\displaystyle U_{x}=\exp \left\{-i\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt\cdot \sigma _{x}/2\right\}=e^{-i\pi \sigma _{x}/2}=-i\sigma _{x}}$

up to the global phase ${\displaystyle -i}$ and is known as the NOT gate.

The ability to couple qubits is essential for implementing 2-qubit gates. Coupling two qubits can be achieved by connecting both to an intermediate electrical coupling circuit. The circuit may be either a fixed element (such as a capacitor) or be controllable (like the DC-SQUID). In the first case, decoupling qubits during the time the gate is switched off is achieved by tuning qubits out of resonance one from another, making the energy gaps between their computational states different.^[41] This approach is inherently limited to nearest-neighbor coupling since a physical electrical circuit must be laid out between connected qubits. Notably, D-Wave Systems' nearest-neighbor coupling achieves a highly connected unit cell of 8 qubits in Chimera graph configuration. Quantum algorithms typically require coupling between arbitrary qubits. Consequently, multiple swap operations are necessary, limiting the length of quantum computation possible before processor decoherence.

Another method of coupling two or more qubits is by way of a quantum bus, by pairing qubits to this intermediate. A quantum bus is often implemented as a microwave cavity modeled by a quantum harmonic oscillator. Coupled qubits may be brought in and out of resonance with the bus and with each other, eliminating the nearest-neighbor limitation. Formalism describing coupling is cavity quantum electrodynamics. In cavity quantum electrodynamics, qubits are analogous to atoms interacting with an optical photon cavity with a difference of GHz (rather than the THz regime of electromagnetic radiation). Resonant excitation exchange among these artificial atoms is potentially useful for direct implementation of multi-qubit gates.^[42] Following the dark state manifold, the Khazali-Mølmer scheme^[42] performs complex multi-qubit operations in a single step, providing a substantial shortcut to the conventional circuit model.

One popular gating mechanism uses two qubits and a bus, each tuned to different energy level separations. Applying microwave excitation to the first qubit, with a frequency resonant with the second qubit, causes a ${\displaystyle \sigma _{x}}$ rotation of the second qubit. Rotation direction depends on the state of the first qubit, allowing a controlled phase gate construction.^[43]

Following the notation of,^[43] the drive Hamiltonian describing the excited system through the first qubit driving line is formally written

${\displaystyle H_{D}/\hbar =A(t)\cos({\tilde {\omega }}_{2}t)\left(\sigma _{x}\otimes I-{\frac {J}{\Delta _{12}}}\sigma _{z}\otimes \sigma _{x}+m_{12}I\otimes \sigma _{x}\right)}$,

where ${\displaystyle A(t)}$ is the shape of the microwave pulse in time, ${\displaystyle {\tilde {\omega }}_{2}}$ is resonance frequency of the second qubit, ${\displaystyle \{I,\sigma _{x},\sigma _{y},\sigma _{z}\}}$ are the Pauli matrices, ${\displaystyle J}$ is the coupling coefficient between the two qubits via the resonator, ${\displaystyle \Delta _{12}\equiv \omega _{1}-\omega _{2}}$ is qubit detuning, ${\displaystyle m_{12}}$ is stray (unwanted) coupling between qubits, and ${\displaystyle \hbar }$ is the reduced Planck constant. The time integral over ${\displaystyle A(t)}$ determines the angle of rotation. Unwanted rotations from the first and third terms of the Hamiltonian can be compensated for with single qubit operations. The remaining component, combined with single qubit rotations, forms a basis for the su(4) Lie algebra.

Higher levels (outside of the computational subspace) of a pair of coupled superconducting circuits can be used to induce a geometric phase on one of the computational states of the qubits. This leads to an entangling conditional phase shift of the relevant qubit states. This effect has been implemented by flux-tuning the qubit spectra ^[44] and by using selective microwave driving.^[45] Off-resonant driving can be used to induce differential ac-Stark shift, allowing the implementation of all-microwave controlled-phase gates.^[46]

The Heisenberg model of interactions, written as

${\displaystyle {\hat {\mathcal {H}}}_{\mathrm {XXZ} }/\hbar =\sum _{i,j}J_{\mathrm {XY} }({\hat {\sigma }}_{\text{x}}^{i}{\hat {\sigma }}_{\text{x}}^{j}+{\hat {\sigma }}_{\text{y}}^{i}{\hat {\sigma }}_{\text{y}}^{j})+J_{\mathrm {ZZ} }{\hat {\sigma }}_{\text{z}}^{i}{\hat {\sigma }}_{\text{z}}^{j}}$,

serves as the basis for analog quantum simulation of spin systems and the primitive for an expressive set of quantum gates, sometimes referred to as fermionic simulation (or fSim) gates. In superconducting circuits, this interaction model has been implemented using flux-tunable qubits with flux-tunable coupling,^[47] allowing the demonstration of quantum supremacy.^[48] In addition, it can also be realized in fixed-frequency qubits with fixed-coupling using microwave drives.^[49] The fSim gate family encompasses arbitrary XY and ZZ two-qubit unitaries, including the iSWAP, the CZ, and the SWAP gates (see Quantum logic gate).

Architecture-specific readout, or measurement, mechanisms exist. Readout of a phase qubit is explained in the qubit archetypes table above. A flux qubit state is often read using an adjustable DC-SQUID magnetometer. States may also be measured using an electrometer.^[1] A more general readout scheme includes a coupling to a microwave resonator, where resonance frequency of the resonator is dispersively shifted by the qubit state.^[50][51] Multi-level systems (qudits) can be readout using electron shelving.^[52]

DiVincenzo's criteria is a list describing the requirements for a physical system to be capable of implementing a logical qubit. DiVincenzo's criteria is satisfied by superconducting quantum computing implementation. Much of the current development effort in superconducting quantum computing aim to achieve interconnect, control, and readout in the 3rd dimension with additional lithography layers.The list of DiVincenzo's criteria for a physical system to implement a logical qubit is satisfied by the implementation of superconducting qubits. Although DiVincenzo's criteria as originally proposed consists of five criteria required for physically implementing a quantum computer, the more complete list consists of seven criteria as it takes into account communication over a computer network capable of transmitting quantum information between computers, known as the “quantum internet”. Therefore, the first five criteria ensure successful quantum computing, while the final two criteria allow for quantum communication.

1. A scalable physical system with well characterized qubits. "Well characterized implies that that Hamiltonian function must be well-defined i.e. the energy eigenstates of the qubit should be able to be quantified.. A scalable system is self-explanatory, it indicates that this ability to regulate a qubit should be augmentable for multiple more qubits. Herein lies the major issue Quantum Computers face, as more qubits are implemented it leads to an exponential increase in cost and other physical implementations which pale in comparison to the enhanced speed it may offer.^[11] As superconducting qubits are fabricated on a chip, the many-qubit system is readily scalable. Qubits are allocated on the 2D surface of the chip. The demand for well characterized qubits is fulfilled with (a) qubit non-linearity (accessing only two of the available energy levels) and (b) accessing a single qubit at a time (rather than the entire many-qubit system) by way of per-qubit dedicated control lines and/or frequency separation, or tuning out, of different qubits.
2. Ability to initialize the state of qubits to a simple fiducial state.^[53] A fiducial state is one that is easily and consistently replicable and is useful in quantum computing as it may be used to guarantee the initial state of qubits. One simple way to initialize a superconducting qubit is to wait long enough for the qubits to relax to the ground state. Controlling qubit potential with tuning knobs allows faster initialization mechanisms.
3. Long relevant decoherence times^[53]. Decoherence of superconducting qubits is affected by multiple factors. Most decoherence is attributed to the quality of the Josephson junction and imperfections in the chip substrate. Due to their mesoscopic scale, superconducting qubits are relatively short lived. Nevertheless, thousands of gate operations have been demonstrated in these many-qubit systems.^[54] Recent strategies to improve device coherence include purifying the circuit materials and designing qubits with decreased sensitivity to noise sources.^[24]
4. A "universal" set of quantum gates.^[53] Superconducting qubits allow arbitrary rotations in the Bloch sphere with pulsed microwave signals, implementing single qubit gates. ${\displaystyle \sigma _{z}\sigma _{z}}$ and ${\displaystyle \sigma _{x}\sigma _{x}}$ couplings are shown for most implementations and for complementing the universal gate set.^[55][56][49] This criterion may also be satisfied by coupling two transmons with a coupling capacitor.^[1]
5. Qubit-specific measurement ability.^[53] In general, single superconducting qubits are used for control or for measurement.
6. Interconvertibility of stationary and flying qubits.^[53] While stationary qubits are used to store information or perform calculations, flying qubits transmit information macroscopically. Qubits should be capable of converting from being a stationary qubit to being a flying qubit and vice versa.
7. Reliable transmission of flying qubits between specified locations.^[53]

The final two criteria have been experimentally proven by research performed by ETH with two superconducting qubits connected by a coaxial cable.^[57]

One of the primary challenges of superconducting quantum computing is the extremely low temperatures at which superconductors like Bose-Einstein Condensates exist. Other basic challenges in superconducting qubit design are shaping the potential well and choosing particle mass such that energy separation between two specific energy levels is unique, differing from all other interlevel energy separation in the system, since these two levels are used as logical states of the qubit.

Superconducting quantum computing must also mitigate quantum noise (disruptions of the system caused by its interaction with an environment) as well as leakage (information being lost to the surrounding environment). One way to reduce leakage is with parity measurements.^[16] Another strategy is to use qubits with large anharmonicity.^[26][27] Many current challenges faced by superconducting quantum computing lie in the field of microwave engineering.^[50] As superconducting quantum computing approaches larger scale devices, researchers face difficulties in qubit coherence, scalable calibration software, efficient determination of fidelity of quantum states across an entire chip, and qubit and gate fidelity.^[16] Moreover, superconducting quantum computing devices must be reliably reproducible at increasingly large scales such that they are compatible with these improvements.^[16]

Journey of superconducting quantum computing:

Although not the newest development, the focus began to shift onto superconducting qubits in the latter half of the 1990s when quantum tunneling across Josephson junctions became apparent which allowed for the realization that quantum computing could be achieved through these superconducting qubits.^[58]

At the end of the century in 1999, a paper^[59] was published by Yasunobu Nakamura, which exhibited the initial design of a superconducting qubit which is now known as the "charge qubit". This is the primary basis point on which later designs amended upon. These initial qubits had their limitations in respect to maintaining long coherence times and destructive measurements. The further amendment to this initial breakthrough lead to the invention of the phase and flux qubit and subsequently resulting in the transmon qubit which is now widely and primarily used in Superconducting Quantum Computing.The transmon qubit has enhanced original designs and has further cushioned charge noise from the qubit.^[58]

The journey has been long, arduous and full of breakthroughs but has seen significant advancements in the recent history and has massive potential for revolutionizing computing.

Future of superconducting quantum computing:

The sector's leading industry giants, like Google, IBM and Baidu, are using superconducting quantum computing and transmon qubits to make leaps and bounds in the area of quantum computing.

In August 2022, Baidu released its plans to build a fully integrated top to bottom quantum computer which incorporated superconducting qubits. This computer will be all encompassing with hardware, software and applications fully integrated. This is a first in the world of quantum computing and will lead to ground-breaking advancements.^[60]

IBM released the following roadmap publicly that they have set for their quantum computers which also incorporated superconducting qubits and the transmon qubit.

2021: In 2021, IBM came out with their 127-qubit processor.^[61]

2022: On November 9, IBM announced its 433 qubit processor called "Osprey".^[62]

2023: IBM plan on releasing their Condor quantum processor with 1,121 qubits.^[61]

2024: IBM plan on releasing their Flamingo quantum processor with 1,386+ qubits.^[61]

2025: IBM plan on releasing their Kookaburra quantum processor with 4,158+ qubits.^[61]

2026 and beyond: IBM plan on releasing a quantum processor that scaled beyond 10,000 qubits to a 100,000 qubits.^[61]

Google in 2016, implemented 16 qubits to convey a demonstration of the Fermi-Hubbard Model. In another recent experiment, Google used 17 qubits to optimize the Sherrington-Kirkpatrick model. Google produced the Sycamore quantum computer which performed a task in 200 seconds that would have taken 10,000 years on a classical computer.^[63]

• Stancil, Daniel D.; Byrd, Gregory T. (2022). Principles of Superconducting Quantum Computers (1st ed.). Hoboken, New Jersey: John Wiley & Sons. ISBN 978-1-119-75072-7. OCLC 1302334194. 978-1-119-75074-1 (ebook).
• Salari, Alan (2024). Microwave Techniques in Superconducting Quantum Computers (Unabridged edition). Boston: Artech House. ISBN 978-1-63081-987-3. OCLC 1405187817. 978-1-63081-988-0 (ebook).

• IBM Quantum offers access to over 20 quantum computer systems.
• The IBM Quantum Experience offers free access to writing quantum algorithms and executing them on 5 qubit quantum computers.
• IBM's roadmap for quantum computing shows 65 qubit systems available in 2020 and 127 qubits to be available sometime in 2021.