Logit
 From Wikipedia (De) - Reading time: 2 min
From Wikipedia (De) - Reading time: 2 min
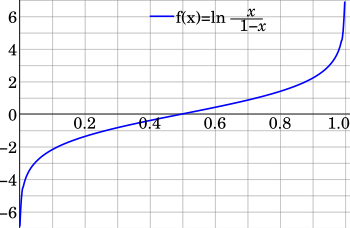
Ein Logit ist in der Statistik der natürliche Logarithmus einer Chance, d. h. der Wahrscheinlichkeit geteilt durch die Gegenwahrscheinlichkeit . Unter der Logit-Transformation versteht man die Transformation von Wahrscheinlichkeiten in Logits. Diese wird in der logistischen Regression zur Spezifikation der Kopplungsfunktion verwendet.
Definition
[Bearbeiten | Quelltext bearbeiten]Ein Logit ist der natürliche Logarithmus einer Chance (Wahrscheinlichkeit durch Gegenwahrscheinlichkeit , engl. odds) für eine Wahrscheinlichkeit [1], d. h.
Die Funktion heißt Logit-Funktion. Wenn Wahrscheinlichkeiten in transformiert werden, spricht man auch von einer Logit-Transformation.
Eigenschaften
[Bearbeiten | Quelltext bearbeiten]- Die Logit-Funktion kann auch mit dem Areatangens Hyperbolicus dargestellt werden,
- Es gilt
- Die Logit-Funktion besitzt die Symmetrieeigenschaft
- Die Logit-Funktion ist differenzierbar und hat die Ableitungsfunktion
- Die Logit-Funktion ist invertierbar. Die Umkehrfunktion der Logit-Funktion ist die logistische Funktion (manchmal auch Expit oder Sigmoid genannt):
- .
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Anwendung
[Bearbeiten | Quelltext bearbeiten]Die Logit-Funktion kann zur Linearisierung von sigmoiden Kurven verwendet werden und hat daher eine große Bedeutung für die Auswertung von ELISA-Kurven in der Biochemie erlangt.
Die Logit-Transformation ist von zentraler Bedeutung für die logistische Regression.
Weblinks
[Bearbeiten | Quelltext bearbeiten]Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Torsten Becker et al.: Stochastische Risikomodellierung und statistische Methoden. Springer Spektrum, 2016. S. 310.
 KSF
KSF










