Bicono
 From Wikipedia (Es) - Reading time: 2 min
From Wikipedia (Es) - Reading time: 2 min
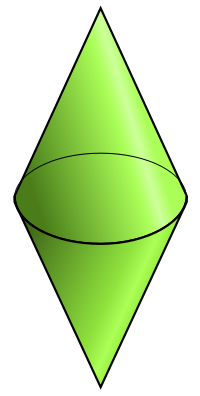
En geometría, un bicono[1] o dicono (de en latín: bi- y griego: di-, ambos significan "dos") es la superficie de revolución tridimensional formada por un rombo alrededor de uno de sus ejes de simetría especular. De manera equivalente, un bicono es la superficie creada al unir dos conos circulares rectos congruentes por sus bases.
Un bicono tiene simetría esférica y simetría bilateral ortogonal.
Geometría
[editar]Para un bicono circular con radio R y altura desde el centro hasta la parte superior H, la fórmula para el volumen se convierte en
Para un bicono circular recto, el área de la superficie es
- donde es la longitud de la generatriz del cono.
Ambas fórmulas se deducen directamente de duplicar las correspondientes al cono.[2]
Aplicaciones
[editar]Biconos y bipirámides se utilizan para asociar recintos convexos en tres dimensiones a circunferencias y polígonos respectivamente.[3]
Otros bi-poliedros
[editar]El bicono es el caso límite de una bipirámide cuando su número de lados tiende a infinito:
| Nombre de la bipirámide | Bipirámide digonal | Bipirámide triangular (véase: J12) |
Octaedro (véase: O) |
Bipirámide pentagonal (véase: J13) |
Bipirámide hexagonal | Bipirámide heptagonal | Bipirámide octogonal | Bipirámide | Bipirámide decagonal | ... | Bipirámide apeirogonal |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Imagen del poliedro | 
|

|

|

|

|

|
... | ||||
| Imagen del poliedro esférico | 
|

|

|

|

|

|

|

|

|
Imagen del teselado | |
| Configuración de vértices |
V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 | ... | V∞.4.4 |
| Diagrama de Coxeter-Dynkin | ... |
Véase también
[editar]Referencias
[editar]- ↑ A. Shubnikov, Aleksej Vasil'evič forme avant 2007 Šubnikov, Vladimir Aleksandrovich Kopt͡sik (1974). Symmetry in Science and Art. Plenum Press. p. 420. ISBN 9780306307591. Consultado el 10 de enero de 2022.
- ↑ Efraín Soto Apolinar (2019). Áreas y volúmenes. Efrain Soto Apolinar. pp. 32 de 41. Consultado el 10 de enero de 2022.
- ↑ Discrete Geometry and Optimization. Springer Science & Business Media. 2013. pp. 125 de 336. ISBN 9783319002002. Consultado el 10 de enero de 2022.
Enlaces externos
[editar]- Weisstein, Eric W. «Bicone». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
 KSF
KSF

