Binomio

En álgebra, un binomio consta únicamente de una suma o resta de dos monomios.

1. ${\displaystyle a+b}$.
2. ${\displaystyle a^{2}b^{5}c^{2}z-b^{3}c^{9}d^{2}}$.
3. ${\displaystyle 3\tan ^{2}\phi \,-\,{\frac {b^{2}}{e^{i\pi \theta }}}}$: es una diferencia de expresiones trigonométricas.

1. ${\displaystyle x^{2}+y^{2}}$. Suma de cuadrados.
2. ${\displaystyle x^{2}-y^{2}}$. Diferencia de cuadrados.
3. ${\displaystyle x^{3}+y^{3}}$. Suma de cubos.
4. ${\displaystyle x^{3}-y^{3}}$. Diferencia de cubos.
5. ${\displaystyle x^{n}+y^{n}}$. Suma de n-esimas potencias.^[1]​
6. ${\displaystyle x^{n}-y^{n}}$. Diferencia de n-ésimas potencias.^[2]​

El resultado de multiplicar un binomio a+b con un monomio c se obtiene aplicando la propiedad distributiva del producto respecto de la adición:

${\displaystyle c(a+b)=ca+cb}$

o realizando la operación:

${\displaystyle {\begin{array}{rrr}&a&+b\\\times &&c\\\hline &ca&+cb\end{array}}}$

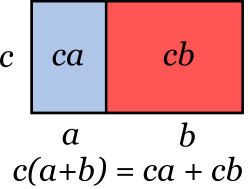
Esta operación tiene una interpretación geométrica ilustrada en la figura. El área del rectángulo es c(a+b) (el producto de la base por la altura), pero también puede obtenerse como la suma de las dos áreas(ca y cb).

Ejemplo:

${\displaystyle 3x(4x-6y)=(3x)(4x)+(3x)(-6y)=12x^{2}-18xy}$

O también:

${\displaystyle {\begin{array}{rrr}&4x&-6y\\\times &&3x\\\hline &12x^{2}&-18xy\end{array}}}$

El binomio ${\displaystyle a^{2}-b^{2}}$ puede factorizarse como el producto de dos binomios:

${\displaystyle a^{2}-b^{2}=(a-b)(a+b)}$.

Demostración:

${\displaystyle {\begin{array}{rrr}&a&+b\\\times &a&-b\\\hline &-ab&-b^{2}\\a^{2}&+ab&\\\hline a^{2}&&-b^{2}\end{array}}}$b²+a²

Esta disposición suele llamarse diferencia de cuadrados, y es un caso especial de la fórmula: ${\displaystyle a^{n+1}-b^{n+1}=(a-b)\sum _{k=0}^{n}a^{k}\,b^{n-k}}$.

El producto de un par de binomios lineales ${\displaystyle (ax+b)}$ ${\displaystyle (cx+d)}$ es:

${\displaystyle (ax+b)(cx+d)=acx^{2}+axd+bcx+bd=acx^{2}+(ad+bc)x+bd}$

${\displaystyle {\begin{array}{rrr}&ax&+b\\\times &cx&+d\\\hline &adx&+bd\\acx^{2}&+bcx&\\\hline acx^{2}&+(ad+bc)x&+bd\end{array}}}$

Un binomio elevado a la n-ésima potencia, se escribe:${\displaystyle (a+b)^{n}}$, y puede desarrollarse utilizando la fórmula de teorema de Newton o, equivalentemente, con ayuda del triángulo de Pascal. El ejemplo más sencillo es el cuadrado perfecto: ${\displaystyle (p+q)^{2}}$

Al elevar un binomio al cuadrado, se lo multiplica por sí mismo:

${\displaystyle (a+b)^{2}=(a+b)(a+b)=a^{2}+2ab+b^{2}}$.

La operación se efectúa del siguiente modo:

${\displaystyle {\begin{array}{rrr}&a&+b\\\times &a&+b\\\hline &+ab&+b^{2}\\a^{2}&+ab&\\\hline a^{2}&+2ab&+b^{2}\end{array}}}$

De aquí se puede derivar una regla para el cálculo directo: se suman los cuadrados de cada término con el doble producto de los mismos.

Un trinomio de la forma ${\displaystyle a^{2}+2ab+b^{2}}$, se conoce como trinomio cuadrado perfecto;

Cuando el segundo término es negativo:

${\displaystyle (a-b)^{2}=(a-b)(a-b)=a^{2}-2ab+b^{2}}$

La operación se efectúa del siguiente modo:

${\displaystyle {\begin{array}{rrr}&a&-b\\\times &a&-b\\\hline &-ab&+b^{2}\\a^{2}&-ab&\\\hline a^{2}&-2ab&+b^{2}\end{array}}}$

Ejemplo:

${\displaystyle (2x-3y)^{2}=(2x)^{2}+2(2x)(-3y)+(-3y)^{2}=4x^{2}-12xy+9y^{2}}$

Si se quiere hallar la derivada de la función cuadrática ${\displaystyle y=x^{2}}$, se desarrolla el binomio ${\displaystyle {(x+h)}^{2}=x^{2}+2xh+h^{2}}$. El coeficiente del término en ${\displaystyle h}$ que es ${\displaystyle 2x}$ es la derivada de ${\displaystyle x^{2}}$. Obsérvese que si consideramos el trinomio del desarrollo como dependiente de ${\displaystyle h}$, el término lineal es ${\displaystyle 2xh}$.

Igualmente, para ${\displaystyle y=x^{3}}$ se desarrolla ${\displaystyle (x+h)^{3}}$. En el cuatrinomio resultante, el coeficiente de ${\displaystyle h}$ es ${\displaystyle 3x^{2}}$, que es la derivada de ${\displaystyle x^{3}}$.

• Teorema del binomio
• Monomio
• Trinomio
• Polinomio
• Factorización
• Productos notables
• Completar el cuadrado

• Hazewinkel, Michiel, ed. (2001), «http://www.encyclopediaofmath.org/index.php?title=Binomial&oldid=13725», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .
• Weisstein, Eric W. «Binomial». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Wentworth, George; Smith, David Eugene (1917). Ginn & Co, ed. Elementos de Álgebra (2a edición). Boston, USA. p. 456. 
• Archivo gratuito para construir tridimensionalmente el cubo del binomio https://www.thingiverse.com/thing:2797705 Archivado el 19 de febrero de 2018 en Wayback Machine.

• Wikcionario tiene definiciones y otra información sobre binomio.