Chaflán (geometría)

Cubo sin achaflanar, ligeramente achaflanado y achaflanado

Modelos de cristal históricos de sólidos platónicos ligeramente achaflanados

En geometría, el chaflán, achaflanado, biselado o truncamiento de aristas es un operador topológico que modifica un poliedro en otro. Es similar a la expansión, separando las caras de una figura hacia afuera, pero mantiene los vértices originales. Para poliedros, esta operación agrega una nueva cara hexagonal que sustituye a cada arista original.

En la notación de poliedros de Conway se representa con la letra c. Un poliedro con e aristas tendrá una forma achaflanada que contiene 2e vértices nuevos, y 3e aristas nuevas y e caras hexagonales nuevas.

En los apartados siguientes se describen en detalle los chaflanes de los cinco sólidos platónicos. Cada uno se muestra en una versión con aristas de igual longitud y en una versión canónica donde todas las aristas tocan la misma interesfera (solo se aprecian como notablemente diferentes en el caso de los sólidos que contienen triángulos). Los poliedros conjugados que se muestran son duales a las versiones canónicas.

Original	{3,3}	{4,3}	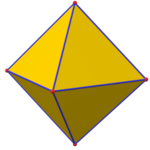{3,4}	{5,3}	{3,5}
Achaflanado

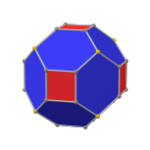
Tetraedro achaflanado
(Con todas las aristas de igual longitud)
Notación de Conway	cT
Poliedro de Goldberg	GPIII(2,0)= {3+,3}2,0
Caras	4 triángulos 6 hexágonos
Aristas	24 (2 tipos)
Vértices	16 (2 tipos)
Configuración de vértices	(12) 3.6.6 (4) 6.6.6
Grupo de simetría	Tetraédrico (Td)
Poliedro conjugado	Triaquis tetratetraedro alternado
Propiedades	Convexo, caras equiláteras
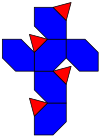Desarrollo

El tetraedro achaflanado (o cubo truncado alternado) es un poliedro convexo construido mediante una operación de alternado de un cubo truncado o como el achaflanado de un tetraedro, reemplazando sus 6 aristas por hexágonos.

Es el poliedro de Goldberg G_III(2,0), que contiene caras triangulares y hexagonales.

Tetraedros achaflanados y sólidos relacionados

Tetraedro achaflanado (canónico)	Dual del tetratetraedro	Tetraedro achaflanado (canónico)
Triaquis tetratetraedro alternado	Octaedro	Triaquis tetratetraedro alternado

Cubo achaflanado
(Con todas las aristas de igual longitud)
Notación de Conway	cC= t4daC
Poliedro de Goldberg	GPIV(2,0)= {4+,3}2,0
Caras	6 cuadrados 12 hexágonos
Aristas	48 (2 tipos)
Vértices	32 (2 tipos)
Configuración de vértices	(24) 4.6.6 (8) 6.6.6
Simetría	Oh, [4,3], (*432) Th, [4,3+], (3*2)
Poliedro conjugado	Tetraquis cuboctaedro
Propiedades	Convexo, caras equiláteras
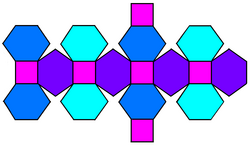Desarrollo

El cubo achaflanado es un poliedro convexo con 32 vértices, 48 ​​aristas y 18 caras (12 hexágonos y 6 cuadrados). Se construye mediante el achaflanado de un cubo. Los cuadrados se reducen de tamaño y se añaden nuevas caras hexagonales sustituyendo a las aristas originales. Su dual es el tetraquis cuboctaedro.

También se le llama incorrectamente dodecaedro rómbico truncado, aunque ese nombre sugiere más bien un rombicuboctaedro. Se puede llamar con más precisión dodecaedro rómbico tetratruncado porque solo los vértices de orden 4 están truncados.

Las caras hexagonales son equiláteras pero no regulares. Están formadas por un rombo truncado, tienen 2 ángulos internos de unos 109,47° ${\displaystyle \cos ^{-1}(-{\frac {1}{3}})}$ y 4 ángulos internos de unos 125,26°, mientras que un hexágono regular tendría todos los ángulos de 120°.

Como todas sus caras tienen un número par de lados con simetría de rotación de 180°, es un zonoedro. También es un poliedro de Goldberg GP_IV(2,0) o {4+,3}_2,0, que contiene caras cuadradas y hexagonales.

El cubo biselado es la suma de Minkowski de un dodecaedro rómbico y un cubo de lado 1 cuando ocho vértices del dodecaedro rómbico están en ${\displaystyle (\pm 1,\pm 1,\pm 1)}$ y sus seis vértices están en las permutaciones de ${\displaystyle (\pm {\sqrt {3}},0,0)}$.

Se puede construir un equivalente de topológico con simetría tetraédrica y caras rectangulares achaflanando los bordes axiales de un dodecaedro. Esta configuración es frecuente en los cristales de pirita.

Piritoedro original y con sus ejes auxiliares truncados

Modelos cristalográficos históricos

Octaedro achaflanado y sólidos relacionados

Cubo achaflanado (canónico)	Rombododecaedro	Octaedro achaflanado (canónico)
Tetraquis cuboctaedro	Cuboctaedro	Triaquis cuboctaedro

Octaedro achaflanado
(Con todas las aristas de igual longitud)
Notación de Conway	cO= t3daO
Caras	8 triángulos 12 hexágonos
Aristas	48 (2 tipos)
Vértices	30 (2 tipos)
Configuración de vértices	(24) 3.6.6 (6) 6.6.6
Simetría	Oh, [4,3], (*432)
Poliedro conjugado	Triaquis cuboctaedro
Propiedades	Convexo

En geometría, el octaedro achaflanado es un poliedro convexo que se puede construir a partir de un rombododecaedro por truncado de sus 8 vértices de orden 3.

También se le puede llamar dodecaedro rómbico tritruncado, en referencia al mencionado truncado de los vértices de orden 3 del rombododecaedro.

Los 8 vértices se truncan de manera que todas las aristas tienen la misma longitud. Las 12 caras rómbicas originales se convierten en hexágonos planos y los vértices truncados se convierten en triángulos.

Las caras hexagonales son equiláteras pero no regulares.

Modelos históricos de un triaquis cuboctaedro y de un octaedro achaflanado

Dodecaedro achaflanado
(Con todas las aristas de igual longitud)
Notación de Conway	cD]= t5daD= dk5aD
Goldberg polyhedron	GV(2,0)= {5+,3}2,0
Fullereno	C80[1]​
Caras	12 pentágonos 30 hexágonos
Aristas	120 (2 tipos)
Vértices	80 (2 tipos)
Configuración de vértices	(60) 5.6.6 (20) 6.6.6
Grupo de simetría	Icosaédrica (Ih)
Poliedro conjugado	Pentaquis icosidodecaedro
Propiedades	Convexo, caras equiláteras

El dodecaedro achaflanado es un poliedro convexo con 80 vértices, 120 aristas y 42 caras: 30 hexágonos y 12 pentágonos. Se construye como un achaflanado de un dodecaedro regular. Los pentágonos se reducen de tamaño y se añaden nuevas caras hexagonales en lugar de todas las aristas originales. Su dual es el pentaquis icosidodecaedro.

También se le llama incorrectamente triacontaedro rómbico truncado, aunque ese nombre sugiere más bien un rombicosidodecaedro. Se puede llamar con más precisión un triacontaedro rómbico pentatruncado porque solo los vértices de orden 5 están truncados.

Icosaedro achaflanado y sólidos relacionados

Dodecaedro achaflanado (canónico)	Triacontaedro rómbico	Icosaedro achaflanado (canónico)
Pentaquis icosidodecaedro	Icosidodecaedro	Triaquis icosidodecaedro

Icosaedro achaflanado
(Con todas las aristas de igual longitud)
Notación de Conway	cI= t3daI
Caras	20 triángulos 30 hexágonos
Aristas	120 (2 tipos)
Vértices	72 (2 tipos)
Configuración de vértices	(24) 3.6.6 (12) 6.6.6
Simetría	Ih, [5,3], (*532)
Poliedro conjugado	Triaquis icosidodecaedro
Propiedades	Convexo

En geometría, el icosaedro achaflanado es un poliedro convexo construido a partir del triacontaedro rómbico por truncado de los 20 vértices de orden 3. Las caras hexagonales pueden ser equiláteras pero no regulares.

También se le puede llamar triacontaedro rómbico tritruncado, en referencia a un truncamiento de los vértices de orden 3 del triacontaedro rómbico.

Teselados ​​regulares y cuasirregulares achaflanados

Teselado cuadrado, Q {4,4}	Teselado triangular, Δ {3,6}	Teselado hexagonal, H {6,3}	Teselado rómbico, daH dr{6,3}
cQ	cΔ	cH	cdaH

La operación de achaflanado aplicada en serie crea poliedros progresivamente más grandes con nuevas caras hexagonales que reemplazan las aristas de la figura original. El operador de achaflanado transforma GP(m,n) en GP(2m,2n).

Un poliedro regular, GP(1,0), crea una secuencia de poliedros de Goldberg: GP(1,0), GP(2,0), GP(4,0), GP(8,0), GP(16,0) ...

	GP(1,0)	GP(2,0)	GP(4,0)	GP(8,0)	GP(16,0)...
GPIV {4+,3}	C	cC	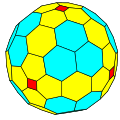ccC	cccC
GPV {5+,3}	D	cD	ccD	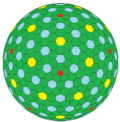cccD	ccccD
GPVI {6+,3}	H	cH	ccH	cccH	ccccH

El octaedro truncado o el icosaedro truncado, GP(1,1) crean una secuencia de Goldberg: GP(1,1), GP(2,2), GP(4,4), GP(8,8)....

	GP(1,1)	GP(2,2)	GP(4,4)...
GPIV {4+,3}	tO	ctO	cctO
GPV {5+,3}	tI	ctI	cctI
GPVI {6+,3}	tH	ctH	cctH

Un tetraquishexaedro o un pentaquisdodecaedro truncados, GP(3,0), crean una secuencia de Goldberg: GP(3,0), GP(6,0), GP(12,0)...

	GP(3,0)	GP(6,0)	GP(12,0)...
GPIV {4+,3}	tkC	ctkC	cctkC
GPV {5+,3}	tkD	ctkD	cctkD
GPVI {6+,3}	tkH	ctkH	cctkH

Al igual que la operación de expansión, el achaflanado se puede aplicar a cualquier dimensión. Para polígonos, triplica el número de vértices. Para policoros, se crean nuevas celdas alrededor de los bordes originales. Las celdas son prismas que contienen dos copias de la cara original, con pirámides aumentadas en los lados del prisma.

• Notación de poliedros de Conway
• Sólido casi coincidente de Johnson
• Canteado (geometría)

• Goldberg, Michael (1937). «A class of multi-symmetric polyhedra». Tohoku Mathematical Journal 43: 104-108. 
• Joseph D. Clinton, Conjetura del ángulo central igual de Clinton [1]
• Hart, George (2012). «Goldberg Polyhedra». En Senechal, Marjorie, ed. Shaping Space (2nd edición). Springer. pp. 125–138. ISBN 978-0-387-92713-8. doi:10.1007/978-0-387-92714-5_9. 
• Hart, George (18 de junio de 2013). «Mathematical Impressions: Goldberg Polyhedra». Simons Science News. 
• Antoine Deza, Michel Deza, Viatcheslav Grishukhin, Fullerenos y poliedros de coordinación versus incrustaciones de medio cubo, 1998 PDF [2] (p. 72 Fig. 26. Tetraedro biselado)
• Deza, A.; Deza, M.; Grishukhin, V. (1998), «Fullerenes and coordination polyhedra versus half-cube embeddings», Discrete Mathematics 192 (1): 41-80, doi:10.1016/S0012-365X(98)00065-X, archivado desde el original el 6 de febrero de 2007 ..

• Tetraedro achaflanado
• Sólidos biselados
• Truncación de vértices y bordes de los sólidos platónicos y de Arquímedes que conducen a poliedros transitivos de vértices Livio Zefiro
• generador poliédrico VRML (Notación de poliedros de Conway)
  • Modelo VRML Cubo biselado
• 3.2.7. Numeración sistemática para (C80-Ih) [5,6] fullerene
• Fullereno C80
  1. [3] (Número 7 -Ih)
  2. [4]
• Cómo hacer un cubo biselado