Estrella (figura geométrica)

Una estrella es cualquier objeto con rayos que parten de un centro común.^[1]​ Con carácter general, la estrella, como objeto matemático, no está definido de forma unívoca. Existen grafos estrellados, polígonos estrellados, estrellas o formas estrelladas y todos ellos tienen definiciones que a veces se solapan o se refieren indistintamente a uno u otro objeto. Así, por ejemplo, se encuentran definiciones que aceptan que las dos figuras de la derecha son polígonos estrellados,^[2]​ mientras que otras solo aceptan como tal a la primera.^[3]​

Además de estas figuras que, de uno u otro modo, pueden quedar bien definidas, se construyen formas estrelladas de otro tipo tomando como base polígonos estrellados o polígonos "normales" mediante la prolongación con distintos criterios de sus lados.

En la naturaleza, el arte, la técnica o la cultura, en general, las estrellas, con distinta precisión geométrica, aparecen con mucha frecuencia.

Dado un punto C en el plano y n puntos P_i, i = 0, 1, ..., n, entre los cuales no hay tres alineados, llamamos grafo estrellado de centro C y n vértices al conjunto de segmentos CP_i. Si los puntos P_i están en los vértices de un polígono regular y C en su centro, se obtienen grafos estrellados regulares.

Así, para n = 0, 1, 2, 3, 4 y 5, se pueden obtener las siguientes figuras:

Otra definición de grafo estrellado coincidiría con la de "haz de segmentos", esto es, un conjunto de segmentos cuyo centro es común en todos ellos.^[4]​ En el gráfico adyacente, solo la figura cuyo fondo es un cuadrado se atiene a esta definición, más estricta.

Si a partir de los vértices de un polígono regular de p lados se unen sus vértices alternadamente, es decir, cada q vértices(orden q) sucesivamente hasta alcanzar el vértice inicial, se obtiene un polígono regular estrellado, cuyos lados y ángulos son todos iguales. La figura que se obtiene puede representarse mediante la expresión {p/q}.

Por ejemplo, a partir de un pentágono regular (p = 5) puede trazarse una estrella de cinco puntas uniendo el primer vértice con el tercero (q = 2), el tercero con el quinto, el quinto con el segundo, el segundo con el cuarto y el cuarto con el primero. Se obtiene así el polígono estrellado {5/2}.

Para generar un polígono estrellado, la fracción p/q debe ser irreducible, esto es, p y q han de ser primos relativos, obteniéndose en tal caso el mismo polígono que en el caso ${\displaystyle {\frac {p}{p-q}}}$ por simple simetría.^[5]​

La notación {p/q} se debe a Ludwig Schläfli.

{5/2}	{7/2}	{7/3}	{8/3}	{9/2}	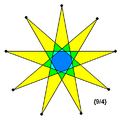{9/4}

Cuando la fracción p/q no es irreducible, los vértices del polígono inicial no quedan todos conectados. Pueden obtenerse entonces figuras denominadas estrellas dando una «segunda vuelta» con los mismos criterios, partiendo del primer vértice no conectado en la primera etapa. Así se obtiene finalmente una figura que también podría construirse mediante la superposición de polígonos girados. Un ejemplo típico sería el de la Estrella de David, construido a partir de un hexágono y de orden {6/2}.

Una definición más laxa admite a los polígonos estrellados y a las estrellas tal y como aquí se han definido dentro de la misma categoría.^[2]​

En el caso de polígonos simples, aquellos que dividen el plano en solo dos regiones (interior y exterior), se considera estrellado todo polígono de vértices P_i, i = 1, ..., n, que tiene al menos un punto en su interior, C, tal que el segmento CP_i está en el interior del polígono.

Esta definición es muy importante en Informática, por diversos motivos.

Consideramos en estos casos un polígono estrellado simple regular a todo aquel cuyos vértices están de forma alternativa sobre dos circunferencias concéntricas, de centro O, siendo los ángulos centrales (P_iOP_i+1, con i = 1, ..., n-1) todos iguales.

Las estrellas de mar y algunas flores son los ejemplos más claros de seres de la naturaleza con forma de estrella. Aunque tienen ese nombre, las estrellas del firmamento son, en realidad, esferas ofreciendo una imagen estrellada solo de forma aparente en determinadas circunstancias. La carambola es una fruta cuya sección es una estrella de cinco puntas. Las hojas de muchas plantas también tienen esta forma.

• 
  Estrellas de mar.
• 
• 
  Flores.
• 
• 
  Carambolo.
• 
  Hojas.

Desde varios siglos antes de Cristo, la secta de los pitagóricos, usaba el llamado "pentagrama" como su emblema. En él aparece la razón aúrea, entre otros conceptos y propiedades matemáticas. El emblema gozaba de un poderoso simbolismo.^[6]​

La estrella tartésica, de ocho puntas, resultado de la superposición de dos cuadrados, era el símbolo con que el pueblo tartésico representaba el sol. Esta estrella, también conocida como octagrama, aparecerá a lo largo de la historia en otros ámbitos (p.e., islam o hinduismo).

La estrella de David, símbolo del judaísmo, es una estrella de seis puntas que puede construirse mediante la superposición de dos triángulos equiláteros. En color amarillo la usaban los nazis para identificar a los judíos entre la población.

La media luna en cuarto creciente y la estrella son símbolos del islam que se han incorporado a diversas banderas nacionales.

La Fe baha'i tiene como símbolo una estrella de nueve puntas.

El satanismo, algunas religiones paganas y otras creencias mágicas y de brujería hacen uso del pentáculo, una estrella de cinco puntas dibujada de un solo trazo, la mayoría de las veces dentro de una circunferencia circunscrita.

• 
  Pitagóricos.
• 
  Estrella tartésica.
• 
  Estrella de David.
• 
  Símbolo del Islam.
• 
  Fe baha'i.
• 
  Pentáculo sagrado de religiones paganas.
• 
  Pentáculo del Sexto Libro de Moisés.
• 
  Pentáculo satánico.

En arquitectura las estrellas se han usado para rosetones de catedrales, edificios, motivos ornamentales, etc. En la Alhambra, por ejemplo, aparecen mosaicos con estrellas que reflejan un profundo conocimiento geométrico de sus autores.^[7]​

• 
  Rosetón
• 
  Mosaicos estrellados en la Alhambra.
• 
• 
  Tragaluces de los baños árabes.

La estrella de cinco puntas es una de las que aparecen con más frecuencia en todo tipo de manifestaciones artísticas y culturales.

• 
  Estrella roja, símbolo del comunismo.
• 
  Estrella en el Paseo de la Fama de Hollywood

En especial, tienen una gran presencia en los logotipos de muchas marcas comerciales. Sirvan los siguientes como ejemplos: Bancaja, Converse, Estrella Damm, Mercedes-Benz, Subaru, Telemadrid...

Hay muchas banderas que contienen estrellas. Las que se muestran a continuación son solo algunos ejemplos:

• 
  Alaska (5 puntas)
• 
  Antigua y Barbuda (media estrella de 16 puntas)
• 
  Aruba (4 puntas)
• 
  Australia (cinco estrellas de siete puntas y una de cinco)
• 
  Azerbaiyán (ocho puntas)
• 
  Bosnia y Herzegovina
• 
  República de Botonia (Micronación)
• 
  Brasil (cinco puntas)
• 
  Burundi (seis puntas)
• 
  Chile
• 
  China
• 
  Comunidad de Madrid
• 
  Corea del Norte
• 
  Cuba
• 
  Estados Unidos de América
• 
  Filipinas (una estrella de ocho puntas y tres de cinco)
• 
  India (24 puntas)
• 
  Islas Marshall (24 puntas)
• 
  Israel
• 
  Jordania (siete puntas)
• 
  Malasia (14 puntas)
• 
  Marruecos
• 
  Antigua bandera mapuche con un guñelve (estrella mapuche de ocho puntas) dentro de un guemil.
• 
  Bandera mapuche con un guñelve, posiblemente utilizada por las tropas mapuches c.siglo XVIII.
• 
  Nauru (12 puntas)
• 
  Nepal (12 puntas)
• 
  Nueva Zelanda
• 
  Ruanda (24 puntas)
• 
  Túnez
• 
  Turquía
• 
  Unión Europea
• 
  Venezuela
• 
  Vietnam

Otros lugares donde aparecen las estrellas son:

• Rangos militares.
• Rosa de los vientos, en la marina.
• Categorías de los hoteles.
• El tablero de las damas chinas.

• 
  Rangos militares
• 
  Rosa de los vientos
• 
  Damas chinas.

• Estrella de David
• Estrella mágica
• Estrella tartésica
• Pentagrama (geometría)
• Polígono simple

• Polígonos estrellados y estrellas
• Construcción de estrellas