Palanca

Este artículo o sección tiene referencias, pero necesita más para complementar su verificabilidad. Busca fuentes: «Palanca» – noticias · libros · académico · imágenes Este aviso fue puesto el 13 de junio de 2018.

La palanca^[1]​^[2]​ es una máquina simple^[3]​^[4]​ cuya función consiste en transmitir fuerza y desplazamiento. Está compuesta por una barra rígida que puede girar libremente alrededor de un punto de apoyo, llamado fulcro.^[5]​

Puede utilizarse para amplificar la fuerza mecánica aplicada a un objeto, para incrementar su velocidad o distancia recorrida, en respuesta a la aplicación de una fuerza.

En las palancas simples existen tres puntos de análisis que deben considerarse: la fuerza aplicada, la reacción (o resistencia) y el punto de apoyo.

El invento de la palanca y su empleo en la vida cotidiana proviene de la época prehistórica. Su empleo cotidiano, en forma de cigoñales, está documentado desde el tercer milenio a. C. —en sellos cilíndricos de Mesopotamia—. El manuscrito más antiguo que se conserva con una mención a la palanca forma parte de la colección matemática de Papo de Alejandría,^[6]​ una obra en ocho volúmenes que se estima fue escrita alrededor del año 340. Allí aparece la famosa cita de Arquímedes:

Dadme un punto de apoyo y moveré el mundo.^[7]​^[8]​^[9]​

La única nota histórica sobre su uso se debe a Plutarco, quien en su obra Vidas paralelas (c. 100 a. C.) relata que Arquímedes, en carta al rey Hierón de Siracusa, a quien le unía gran amistad, afirmó que con una fuerza dada podía mover cualquier peso e incluso se jactó de que si existiera otra Tierra, yendo a ella podría mover esta. Hierón, asombrado, solicitó a Arquímedes que realizara una demostración.

Acordaron que el objeto a mover fuera un barco de la armada del rey, ya que Hierón creía que este no podría sacarse de la dársena y llevarse a dique seco sin el empleo de un gran esfuerzo y numerosos hombres. Según relata Plutarco, tras cargar el barco con muchos pasajeros y con las bodegas repletas, Arquímedes se sentó a cierta distancia y tirando de la cuerda alzó sin gran esfuerzo el barco, sacándolo del agua tan derecho y estable como si aún permaneciera en el mar.

El manuscrito más antiguo que se conserva, y que menciona la palanca, es parte de la Sinagoga o Colección Matemática de Papo de Alejandría, una obra en ocho volúmenes que se cree fue escrita alrededor del año 340.^[10]​ En el volumen VIII de esta obra aparece la famosa cita de Arquímedes: «Dadme un punto de apoyo, y moveré el mundo».

A Arquímedes se le atribuye la primera postulación matemática formal del principio de la palanca. Las enseñanzas transmitidas por el griego al volumen I de su obra “Del equilibrio de los planes”, se aprovecharon sin variaciones durante siglos hasta que alguien profundizó sobre la base establecida por los estudios de Arquímedes. En esta obra se desprenden los postulados del equilibrio de sólidos en el plano y se dan diversas proposiciones aplicables. En este caso las proposiciones 6 y 7 son referidas a la palanca, donde suele decirse que se expresa la ley de la palanca.

Aunque las teorías no prosperaron, son destacables los avances en la técnica de las balanzas de brazos iguales, que en la Edad Media perfeccionaron el aparato gracias a la mejora de los ejes, que eran más refinados gracias a la incorporación de un clavo o un bolón atravesado y sujetado gracias a un tenedor.^[11]​

En el ámbito de los avances en la teoría de la palanca, se tuvo que esperar a Leonardo da Vinci, que estudió las diferentes geometrías de esta.^[12]​ Da Vinci introdujo la palanca oblicua.^[13]​ A da Vinci se le atribuyen los notables trabajos que todavía hoy siguen vigentes, en el principio de la palanca con aplicaciones para balanzas con palanca de plataforma y también con palanca múltiple articulada. También es remarcable la tarea del genio al introducir la balanza indicadora.^[12]​^[11]​

El concepto de concatenación de palancas en serie fue introducido en 1743, por el inglés John Wyatt,^[14]​^[11]​ concepto que se aprovechó para construir algunas máquinas con palancas compuestas que permitían incrementar la ventaja mecánica o disponer de mecanismos más complejos basados en la palanca. La máquina de Wyatt se basaba en un conjunto de palancas que sostenían una plataforma en uno de los extremos. Se trataba de un instrumento de medida que aprovechaba la composición de palancas para obtener unas medidas más correctas y un sistema más eficiente.

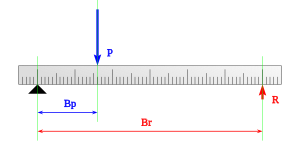
Sobre la barra rígida que constituye una palanca actúan tres fuerzas:^[15]​

• El esfuerzo; P: es la fuerza que aplicamos voluntariamente con el fin de obtener un resultado; ya sea manualmente o por medio de motores u otros mecanismos.
• La resistencia; R: es la fuerza que vencemos, ejercida sobre la palanca por el cuerpo a mover. Su valor será equivalente, por el principio de acción y reacción, a la fuerza transmitida por la palanca a dicho cuerpo.
• La fuerza de apoyo: es la ejercida por el fulcro (punto de apoyo de la barra) sobre la palanca. Si no se considera el peso de la barra, será siempre igual y opuesta a la suma de las anteriores, de tal forma que la palanca se mantiene sin desplazarse del punto de apoyo, sobre el que rota libremente.

Nomenclatura

• Brazo de potencia; Bp: la distancia entre el punto de aplicación de la fuerza de potencia y el punto de apoyo.
• Brazo de resistencia; Br: la distancia entre la fuerza de resistencia y el punto de apoyo.

En física, la ley que relaciona las fuerzas de una palanca en equilibrio se expresa mediante la ecuación:

${\displaystyle P\times Bp=R\times Br}$

Ley de la palanca:^[16]​^[17]​ Potencia por su brazo es igual a resistencia por el suyo.

Siendo P la potencia, R la resistencia, y Bp y Br las distancias medidas desde el fulcro hasta los puntos de aplicación de P y R respectivamente, llamadas brazo de potencia y brazo de resistencia.

Si en cambio una palanca se encuentra rotando aceleradamente, como en el caso de una catapulta, para establecer la relación entre las fuerzas y las masas actuantes deberá considerarse la dinámica del movimiento sobre la base de los principios de conservación de cantidad de movimiento y momento angular.

Las palancas se dividen en tres géneros,^[18]​^[19]​ también llamados grados,^[5]​ dependiendo de la posición relativa de los puntos de aplicación de la potencia y de la resistencia con respecto al fulcro (punto de apoyo). El principio de la palanca es válido indistintamente del tipo que se trate, pero el efecto y la forma de uso de cada uno cambian considerablemente.

En la palanca de primer género/grado, el fulcro se encuentra situado entre la potencia y la resistencia.^[5]​ Se caracteriza en que la potencia puede ser menor que la resistencia, aunque a costa de disminuir la velocidad transmitida y la distancia recorrida por la resistencia.

Ejemplos de este tipo de palanca son el balancín, las tijeras, las tenazas, las pinzas^[18]​ o la catapulta (para ampliar la velocidad). En el cuerpo humano se encuentran varios ejemplos de palancas de primer género, como el conjunto tríceps braquial-codo-antebrazo.

En la palanca de segundo género/grado, la resistencia se encuentra entre la potencia y el fulcro.^[5]​ Se caracteriza en que la potencia es siempre menor que la resistencia, aunque a costa de disminuir la velocidad transmitida y la distancia recorrida por la resistencia. Como ejemplo está la carretilla^[18]​ y el cascanueces manual de tenaza.

En la palanca de tercer género/grado, la potencia se encuentra entre la resistencia y el fulcro. Se caracteriza en que la fuerza aplicada es mayor que la resultante;^[5]​ y se utiliza cuando lo que se requiere es ampliar la velocidad transmitida a un objeto o la distancia recorrida por él.

Ejemplos de este tipo de palanca son el quitagrapas, el palo de hockey, la escoba, la caña de pescar y la pinza de cejas;^[18]​ y en el cuerpo humano, el conjunto codo-bíceps braquial-antebrazo y la articulación temporomandibular.

Las palancas se utilizan, en sus diferentes formatos, en múltiples aplicaciones de la vida cotidiana y también en el diseño de las máquinas más sofisticadas. Esta máquina puede utilizarse para aplicaciones tan sencillas como mover una piedra con la fuerza humana.

Es notable la aplicación de la palanca en los instrumentos de medida, que se debe al equilibrio de cargas que da la palanca para una configuración del fulcro determinada. Los instrumentos más comunes son:

• La balanza: Se trata de una palanca de primer tipo que tiene igual longitud en los dos brazos y que sirve, por tanto, para pesar con cargas iguales o similares.
• La romana: Es una palanca de primer tipo a la que se puede variar el punto de aplicación de la fuerza de potencia.

Debido a su condición de aumentar las fuerzas según la construcción del mecanismo, a menudo se utilizan para elevar cargas a cualquier tipo de obras.

Una aplicación de palanca de primer tipo es la de las pinzas para manipular objetos en las obras. Con las pinzas, la fuerza de cierre la proporciona el mismo peso de la carga al elevarse. La máquina se diseña de tal modo que el mismo peso se transforma en fuerza que tiende a cerrar la pinza, incrementando el coeficiente de fricción µ de la superficie de enganche con el objeto.^[20]​

Destaca el uso de la palanca como instrumento para el cambio de configuración de mecanismos, ya que se encuentra con frecuencia en las aplicaciones con vehículos.

Normalmente, estas palancas suelen cambiar la geometría de otro mecanismo, que variará en su funcionalidad después del cambio. Se pueden ver distintos usos según el medio utilizado:

• En la automoción se utilizan palancas de cambio de marchas, para escoger el grupo reductor (par de engranajes) con el que se engrana directamente el eje motor. Las palancas se utilizan tanto en los automóviles como en las motocicletas.
• En la aeronáutica se utiliza la palanca del timón de dirección, que es un dispositivo que permite conseguir ventaja mecánica con una geometría de palanca que el piloto puede mover con los pies. Esta palanca puede atarse mediante cables con otra palanca que transmite el par torsor al timón de dirección de la aeronave.^[21]​ Se trata de un buen ejemplo de palanca compuesta que puede aplicarse en las pequeñas aeronaves como actuador mecánico.
• En el mundo ferroviario se utilizan palancas de cambio de vía, que sirven para variar la geometría de las vías del ferrocarril de forma manual.

La palanca es un mecanismo muy utilizado en los aparatos de guerra, formando parte de mecanismos muy complejos con una o varias palancas. Podía utilizarse para dar soporte logístico a las operaciones tácticas, dando servicio a las operaciones con montajes de madera o cargas de cañones o sus cureñas, aunque también se han utilizado las palancas como mecanismo principal de armas tales como los trabuquetes.^[13]​ Algunos tipos de ballesta se paraban mediante una palanca. Algunos funcionaban estirando y otros que actuaban empujando. Un sistema parecido es el que usan para cargar algunas escuetas o carabinas de aire comprimido.

• Otros usos en la mecánica.
• En los instrumentos musicales de teclado.
• En los utensilios manuales.
• En la náutica hay una palanca basada en la polea que es una cuerda que ayuda a la maniobra de la vela. También existe el palanquín que usa un sistema de poleas para sacar la barca del agua. Y otro palanquín de poleas para ayudar a controlar el timón.^{[cita requerida]}

• cigoñal
• cuña (máquina)
• plano inclinado
• polea
• tornillo
• tuerca husillo

• James Hopwood Jeans (2016). Historia de la física. Fondo de Cultura Economica. ISBN 978-607-164-483-1. 
• Dzielska, Maria (2006). Hipatia de Alejandría (José Luis López Muñoz, trad.) (2 edición). Ediciones sirueta. ISBN 978-847-844-749-7. 

• Wikimedia Commons alberga una categoría multimedia sobre palancas.
• Aplicación web que representa la ley de la palanca.
• Cómo mover el mundo según Arquímedes.