Parámetro estadístico
 From Wikipedia (Es) - Reading time: 33 min
From Wikipedia (Es) - Reading time: 33 min

En estadística, un parámetro es el número que resume la gran cantidad de datos que pueden derivarse del estudio de una variable estadística.[1] El cálculo de este número está bien definido, usualmente mediante una fórmula aritmética obtenida a partir de datos de la población.[2][3]
Los parámetros estadísticos son una consecuencia inevitable del propósito esencial de la estadística: crear un modelo de la realidad.[4]
El estudio de una gran cantidad de datos individuales de una población puede ser farragoso e inoperativo, por lo que se hace necesario realizar un resumen que permita tener una idea global de la población, compararla con otras, comprobar su ajuste a un modelo ideal, realizar estimaciones sobre datos desconocidos de la misma y, en definitiva, tomar decisiones. A estas tareas contribuyen de modo esencial los parámetros estadísticos.
Por ejemplo, suele ofrecerse como resumen de la juventud de una población la media aritmética de las edades de sus miembros, esto es, la suma de todas ellas, dividida por el total de individuos que componen tal población.
Enfoque descriptivo
[editar]
Un parámetro estadístico es una medida poblacional. Este enfoque es el tradicional de la estadística descriptiva.[5][6][7] En este sentido, su acepción se acerca a la de medida o valor que se compara con otros, tomando una unidad de una determinada magnitud como referencia.
Por su parte, la facción más formal de la estadística, la estadística matemática y también la inferencia estadística utilizan el concepto de parámetro en su acepción matemática más pura, esto es, como variable que define una familia de objetos matemáticos en determinados modelos. Así se habla, por ejemplo, de una distribución normal de parámetros μ y σ como de una determinada familia de distribuciones con una distribución de probabilidad de expresión conocida, en la que tales parámetros definen aspectos concretos como la esperanza, la varianza, la curtosis, etc. Otro ejemplo común en este sentido es el de la distribución de Poisson, determinada por un parámetro, λ; o la distribución binomial, determinada por dos parámetros, n y p. Desde el punto de vista de la estadística matemática, el hecho de que estas distribuciones describan situaciones reales y los citados parámetros signifiquen un resumen de determinado conjunto de datos es indiferente.
Propiedades deseables en un parámetro
[editar]Según Yule[8] un parámetro estadístico es deseable que tenga las siguientes propiedades:
- Se define de manera objetiva, es decir, es posible calcularlo sin ambigüedades, generalmente mediante una fórmula matemática. Por ejemplo, la media aritmética se define como la suma de todos los datos, dividida por el número de datos. No hay ambigüedad: si se realiza ese cálculo, se obtiene la media; si se realiza otro cálculo, se obtiene otra cosa. Sin embargo, la definición de moda como el «valor más frecuente», puede dar lugar a confusión cuando la mayor frecuencia la presentan varios valores distintos.
- No desperdicia, a priori, ninguna de las observaciones. Con carácter general, un parámetro será más representativo de una determinada población, cuántos más valores de la variable estén implicados en su cálculo. Por ejemplo, para medir la dispersión puede calcularse el recorrido, que solo usa dos valores de la variable objeto de estudio, los extremos; o la desviación típica, en cuyo cálculo intervienen todos los datos del eventual estudio.
- Es interpretable, significa algo. La mediana, por ejemplo, deja por debajo de su valor a la mitad de los datos, está justo en medio de todos ellos cuando están ordenados. Esta es una interpretación clara de su significado.
- Es sencillo de calcular y se presta con facilidad a manipulaciones algebraicas. Se verá más abajo que una medida de la dispersión es la desviación media. Sin embargo, al estar definida mediante un valor absoluto, función definida a trozos y no derivable, no es útil para gran parte de los cálculos en los que estuviera implicada, aunque su interpretación sea muy clara.
- Es poco sensible a las fluctuaciones muestrales. Si pequeñas variaciones en una muestra de datos estadísticos influyen en gran medida en un determinado parámetro, es porque tal parámetro no representa con fiabilidad a la población. Así pues es deseable que el valor de un parámetro con esta propiedad se mantenga estable ante las pequeñas oscilaciones que con frecuencia pueden presentar las distintas muestras estadísticas. Esta propiedad es más interesante en el caso de la estimación de parámetros. Por otra parte, los parámetros que no varían con los cambios de origen y escala o cuya variación está controlada algebraicamente, son apropiados en determinadas circunstancias como la tipificación.
Principales parámetros
[editar]Habitualmente se agrupan los parámetros en las siguientes categorías:
- Medidas de posición.[9]
Se trata de valores de la variable estadística que se caracterizan por la posición que ocupan dentro del rango de valores posibles de esta. Entre ellos se distinguen:
- Las medidas de tendencia central: medias, moda y mediana.
- Las medidas de posición no central: cuantiles (cuartiles, deciles y percentiles).
- Medidas de dispersión.[10]
Resumen la heterogeneidad de los datos, lo separados que estos están entre sí. Hay dos tipos, básicamente:
- Medidas de dispersión absolutas, que vienen dadas en las mismas unidades en las que se mide la variable: recorridos, desviaciones medias, varianza, y desviación típica.
- Medidas de dispersión relativa, que informan de la dispersión en términos relativos, como un porcentaje. Se incluyen entre estas el coeficiente de variación, el coeficiente de apertura, los recorridos relativos y el índice de desviación respecto de la mediana.
- Medidas de forma.[11]
Su valor informa sobre el aspecto que tiene la gráfica de la distribución. Entre ellas están los coeficientes de asimetría y los de curtosis.
- Otros parámetros.
Además, y con propósitos más específicos, existen otros parámetros de uso en situaciones muy concretas, como son las proporciones, los números índice, las tasas y el coeficiente de Gini.
Medidas de tendencia central o centralización
[editar]Son valores que suelen situarse cerca del centro de la distribución de datos. Los más destacados son las medias o promedios (incluyendo la media aritmética, la media geométrica y la media armónica), la mediana y la moda.
Media aritmética o promedio
[editar]
La media muestral o media aritmética es, probablemente, uno de los parámetros estadísticos más extendidos.[12] Sus propiedades son:[13]
- Su cálculo es muy sencillo y en él intervienen todos los datos.
- Se interpreta como «punto de equilibrio» o «centro de masas» del conjunto de datos, ya que tiene la propiedad de equilibrar las desviaciones de los datos respecto de su propio valor:
- Minimiza las desviaciones cuadráticas de los datos respecto de cualquier valor prefijado, esto es, el valor de es mínimo cuando . Este resultado se conoce como Teorema de König. Esta propiedad permite interpretar uno de los parámetros de dispersión más importantes: la varianza.
- Se ve afectada por transformaciones afines (cambios de origen y escala), esto es, si
- entonces , donde es la media aritmética de los , para y (números reales).
Este parámetro, aun teniendo múltiples propiedades que aconsejan su uso en situaciones muy diversas, tiene también algunos inconvenientes, como son:
- Para datos agrupados en intervalos (variables continuas), su valor oscila en función de la cantidad y amplitud de los intervalos que se consideren.
- Es una medida a cuyo significado afecta sobremanera la dispersión, de modo que cuanto menos homogéneos son los datos, menos información proporciona. Dicho de otro modo, poblaciones muy distintas en su composición pueden tener la misma media.[14] Por ejemplo, un equipo de baloncesto con cinco jugadores de igual estatura, 1.95, pongamos por caso, tendría una estatura media de 1.95, evidentemente, valor que representa fielmente a esta homogénea población. Sin embargo, un equipo de estaturas más heterogéneas, 2.20, 2.15, 1.95, 1.75 y 1.70, por ejemplo, tendría también, como puede comprobarse, una estatura media de 1.95, valor que no representa a casi ninguno de sus componentes.
- Es muy sensible a los valores extremos de la variable. Por ejemplo, en el cálculo del salario medio de una empresa, el salario de un alto directivo que gane 1 000 000 € tiene tanto peso como el de mil empleados «normales» que ganen 1000 €, siendo la media de aproximadamente 2000 €.
Moda
[editar]La moda es el dato más repetido, el valor de la variable con mayor frecuencia absoluta.[15] En cierto sentido se corresponde su definición matemática con la locución «estar de moda», esto es, ser lo que más se lleva.
Su cálculo es extremadamente sencillo, pues solo necesita de un recuento. En variables continuas, expresadas en intervalos, existe el denominado intervalo modal o, en su defecto, si es necesario obtener un valor concreto de la variable, se recurre a la interpolación.
Sus principales propiedades son:
- Cálculo sencillo.
- Interpretación muy clara.
- Al depender solo de las frecuencias, puede calcularse para variables cualitativas. Es por ello el parámetro más utilizado cuando al resumir una población no es posible realizar otros cálculos, por ejemplo, cuando se enumeran en medios periodísticos las características más frecuentes de determinado sector social. Esto se conoce informalmente como «retrato robot».[16]
Inconvenientes:
- Su valor es independiente de la mayor parte de los datos, lo que la hace muy sensible a variaciones muestrales. Por otra parte, en variables agrupadas en intervalos, su valor depende excesivamente del número de intervalos y de su amplitud.
- Usa muy pocas observaciones, de tal modo que grandes variaciones en los datos fuera de la moda, no afectan en modo alguno a su valor.
- No siempre se sitúa hacia el centro de la distribución.
- Puede haber más de una moda en el caso en que dos o más valores de la variable presenten la misma frecuencia (distribuciones bimodales o multimodales).
Mediana
[editar]La mediana es un valor de la variable que deja por debajo de sí a la mitad de los datos, una vez que estos están ordenados de menor a mayor.[17] Por ejemplo, la mediana del número de hijos de un conjunto de trece familias, cuyos respectivos hijos son: 3, 4, 2, 3, 2, 1, 1, 2, 1, 1, 2, 1 y 1, es 2, puesto que, una vez ordenados los datos: 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 4, el que ocupa la posición central es 2:
En caso de un número par de datos, la mediana no correspondería a ningún valor de la variable, por lo que se conviene en tomar como mediana el valor intermedio entre los dos valores centrales. Por ejemplo, en el caso de doce datos como los anteriores:
Se toma como mediana

Existen métodos de cálculo más rápidos para datos más numerosos (véase el artículo principal dedicado a este parámetro). Del mismo modo, para valores agrupados en intervalos, se halla el «intervalo mediano» y, dentro de este, se obtiene un valor concreto por interpolación.
Propiedades de la mediana como parámetro estadístico:[18]
- Es menos sensible que la media a oscilaciones de los valores de la variable. Un error de transcripción en la serie del ejemplo anterior en, pongamos por caso, el último número, deja a la mediana inalterada.
- Como se ha comentado, puede calcularse para datos agrupados en intervalos, incluso cuando alguno de ellos no está acotado.
- No se ve afectada por la dispersión. De hecho, es más representativa que la media aritmética cuando la población es bastante heterogénea. Suele darse esta circunstancia cuando se resume la información sobre los salarios de un país o una empresa. Hay unos pocos salarios muy altos que elevan la media aritmética haciendo que pierda representatividad respecto al grueso de la población. Sin embargo, alguien con el salario «mediano» sabría que hay tanta gente que gana más dinero que él, como que gana menos.
Sus principales inconvenientes son que en el caso de datos agrupados en intervalos, su valor varía en función de la amplitud de estos. Por otra parte, no se presta a cálculos algebraicos tan bien como la media aritmética.
Medidas de posición no central
[editar]Directamente relacionados con la anterior, se encuentran las medidas de posición no central, también conocidas como cuantiles. Se trata de valores de la variable estadística que dejan por debajo de sí determinada cantidad de los datos. Son, en definitiva, una generalización del concepto de la mediana. Mientras que ésta deja por debajo de sí al 50 % de la distribución, los cuantiles pueden hacerlo con cualquier otro porcentaje.[19] Se denominan medidas de posición porque informan, precisamente, de la posición que ocupa un valor dentro de la distribución de datos.
Tradicionalmente se distingue entre cuartiles, si se divide la cantidad de datos en cuatro partes antes de proceder al cálculo de los valores que ocupan cada posición; deciles, si se divide los datos en diez partes; o percentiles, que dividen la población en cien partes.
Ejemplos: si se dice que una persona, tras un test de inteligencia, ocupa el percentil 75, ello supone que el 75 % de la población tiene un cociente intelectual con un valor inferior al de esa persona. Este criterio se usa por las asociaciones de superdotados, que limitan su conjunto de miembros a aquellas que alcanzan determinado percentil (igual o superior a 98 en la mayoría de los casos).
El ejemplo que se muestra en la imagen de la derecha es el correspondiente al cálculo inverso, esto es, cuando se desea conocer el percentil correspondiente a un valor de la variable, en lugar del valor que corresponde a un determinado percentil.
Otras medidas de posición central son la media geométrica y la media armónica que, aunque tienen determinadas propiedades algebraicas que podrían hacerlas útiles en determinadas circunstancias, su interpretación no es tan intuitiva como la de los parámetros anteriores.[20]
Comentarios sobre las medidas de posición
[editar]Este tipo de parámetros no tienen por qué coincidir con un valor exacto de la variable y, por tanto, tampoco pueden usarse con carácter general para hacer pronósticos. Por ejemplo, si se dice que la media aritmética de los hijos de las familias de un país es de 1.2, no es posible encontrar familias con ese valor en concreto. Un segundo ejemplo: a ninguna fábrica de zapatos se le ocurriría fabricar los suyos con tallas únicamente correspondientes al valor promedio, ni siquiera tienen por qué ser estas tallas las más fabricadas, pues en tal caso sería más apropiado atender a la moda de la distribución de tallas de los eventuales clientes.
La elección de uno u otro parámetro dependerá de cada caso particular, de los valores de la variable y de los propósitos del estudio. Su uso indiscriminado puede ser deliberadamente tendencioso o involuntariamente sesgado, convirtiéndose, de hecho, en un abuso.[21] Puede pensarse, por ejemplo, en la siguiente situación: un empresario publica que el salario medio en su empresa es de 1600 €. A este dato, que en determinadas circunstancias podría considerarse muy bueno, podría llegarse si la empresa tuviese cuatro empleados con salarios de 1000 € mensuales y el salario del jefe, incluido en la media, fuese de 4000 € al mes:[22]
Con carácter general y a modo de resumen podría decirse que la media aritmética es un parámetro representativo cuando la población sigue una distribución normal o es bastante homogénea; en otras situaciones de fuerte dispersión, habría que decantarse por la mediana. La moda es el último recurso (y el único) cuando de describir variables cualitativas se trata.
Medidas de dispersión
[editar]
Las medidas de posición resumen la distribución de datos, pero resultan insuficientes y simplifican excesivamente la información. Estas medidas adquieren verdadero significado cuando van acompañadas de otras que informen sobre la heterogeneidad de los datos. Los parámetros de dispersión miden eso precisamente, generalmente, calculando en qué medida los datos se agrupan en torno a un valor central. Indican, de un modo bien definido, lo homogéneos que estos datos son. Hay medidas de dispersión absolutas, entre las cuales se encuentran la varianza, la desviación típica o la desviación media, aunque también existen otras menos utilizadas como los recorridos o la meda; y medidas de dispersión relativas, como el coeficiente de variación, el coeficiente de apertura o los recorridos relativos. En muchas ocasiones las medidas de dispersión se ofrecen acompañando a un parámetro de posición central para indicar en qué medida los datos se agrupan en torno de él.[23]
Medidas de dispersión absolutas
[editar]Recorridos
[editar]El recorrido o rango de una variable estadística es la diferencia entre el mayor y el menor valor que toma la misma. Es la medida de dispersión más sencilla de calcular, aunque es algo burda porque solo toma en consideración un par de observaciones. Basta con que uno de estos dos datos varíe para que el parámetro también lo haga, aunque el resto de la distribución siga siendo, esencialmente, la misma.
Existen otros parámetros dentro de esta categoría, como los recorridos o rangos intercuantílicos, que tienen en cuenta más datos y, por tanto, permiten afinar en la dispersión. Entre los más usados está el rango intercuartílico, que se define como la diferencia entre el cuartil tercero y el cuartil primero. En ese rango están, por la propia definición de los cuartiles, el 50 % de las observaciones. Este tipo de medidas también se usa para determinar valores atípicos. En el diagrama de caja que aparece a la derecha se marcan como valores atípicos todos aquellos que caen fuera del intervalo , donde y son los cuartiles 1º y 3º, respectivamente, y representa la mitad del recorrido o rango intercuartílico, también conocido como recorrido semiintercuartílico.[24]
Desviaciones medias
[editar]Dada una variable estadística , y un parámetro de tendencia central , se llama desviación de un valor de la variable respecto de , al número . Este número mide lo lejos que está cada dato del valor central , por lo que una media de esas medidas podría resumir el conjunto de desviaciones de todos los datos.
Así pues, se denomina desviación media de la variable respecto de a la media aritmética de las desviaciones de los valores de la variable respecto de , esto es, si...
entonces
De este modo se definen la desviación media respecto de la media o la desviación media respecto de la mediana , cuya interpretación es sencilla en virtud del significado de la media aritmética.[23]
Sin embargo, el uso de valores absolutos impide determinados cálculos algebraicos que obligan a desechar estos parámetros, a pesar de su clara interpretación, en favor de los siguientes.
Varianza y desviación típica
[editar]
Como se vio más arriba, la suma de todas las desviaciones respecto al parámetro más utilizado, la media aritmética, es cero. Por tanto, si se desea una medida de la dispersión sin los inconvenientes para el cálculo que tienen las desviaciones medias, una solución es elevar al cuadrado tales desviaciones antes de calcular el promedio. Así, se define la varianza como:[25]
- ,
o sea, la media de los cuadrados de las desviaciones respecto de la media.
La desviación típica, σ, se define como la raíz cuadrada de la varianza, esto es,
Para variables agrupadas en intervalos, se usan las marcas de clase (un valor apropiado del interior de cada intervalo) en estos cálculos.
Propiedades:[25]
- Ambos parámetros no se alteran con los cambios de origen.
- Si todos los valores de la variable se multiplican por una constante, , la varianza queda multiplicada por .
- En el intervalo se encuentran, al menos, el de las observaciones (véase Desigualdad de Tchebyschev).[26]
Esta última propiedad muestra la potencia del uso conjunto de la media y la desviación típica como parámetros estadísticos, ya que para valores de iguales a 2 y 3, respectivamente, se obtiene que:
- En el intervalo están, al menos, el 75 % de los datos.
- En el intervalo están, al menos, el 89 % de los datos.
Se cumple la siguiente relación entre los parámetros de dispersión:
donde , y son, respectivamente, la desviación media respecto de la mediana, la desviación media respecto de la media y la desviación típica (véase Desviación media).
La media. Es una medida de dispersión que tiene, por su propia definición, las mismas propiedades que la mediana. Por ejemplo, no se ve afectada por valores extremos o atípicos.[27]
Medidas de dispersión relativa
[editar]Son parámetros que miden la dispersión en términos relativos, un porcentaje o una proporción, por ejemplo, de modo que permiten una sencilla comparación entre la dispersión de distintas distribuciones.[28]
Coeficiente de variación de Pearson
[editar]Se define como , donde σ es la desviación típica y es la media aritmética.
Se interpreta como el número de veces que la media está contenida en la desviación típica. Suele darse su valor en tanto por ciento, multiplicando el resultado anterior por cien. De este modo se obtiene un porcentaje de la variabilidad.
Su principal inconveniente es que en el caso de distribuciones cuya media se acerca a cero, su valor tiende a infinito e incluso resulta imposible de calcular cuando la media es cero. Por ello no puede usarse para variables tipificadas.
Coeficiente de apertura
[editar]Se define como el cociente entre los valores extremos de la distribución de datos, esto es, dada una distribución de datos estadísticos , su coeficiente de apertura, es
Se usa para comparar salarios de empresas.
Recorridos relativos
[editar]Dado , el recorrido de una distribución de datos estadísticos, el recorrido relativo, es , donde es la media aritmética de la distribución.
Dada una distribución de datos estadísticos con cuartiles , el recorrido intercuartílico relativo, se define como[29]
Por otra parte, se define el recorrido semiintercuartílico relativo, , como
Índice de desviación respecto a la mediana
[editar]Se define como , donde es la desviación media respecto de la mediana y es la mediana de una distribución de datos estadísticos dada.
Medidas de forma
[editar]
Las medidas de forma caracterizan la forma de la gráfica de una distribución de datos estadísticos. La mayoría de estos parámetros tiene un valor que suele compararse con la campana de Gauss, esto es, la gráfica de la distribución normal, una de las que con más frecuencia se ajusta a fenómenos reales.
Medidas de asimetría
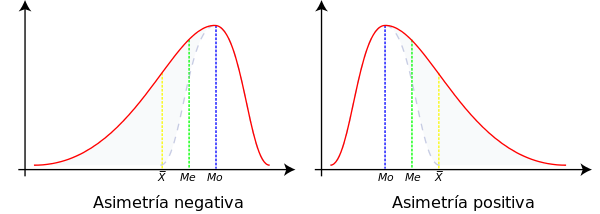
[editar]Se dice que una distribución de datos estadísticos es simétrica cuando la línea vertical que pasa por su media, divide a su representación gráfica en dos partes simétricas. Ello equivale a decir que los valores equidistantes de la media, a uno u otro lado, presentan la misma frecuencia.
En las distribuciones simétricas los parámetros media, mediana y moda coinciden, mientras que si una distribución presenta cierta asimetría, de un tipo o de otro, los parámetros se sitúan como muestra el siguiente gráfico:
Ello puede demostrarse fácilmente si se tiene en cuenta la atracción que la media aritmética siente por los valores extremos, que ya se ha comentado más arriba y las definiciones de mediana (justo en el centro de la distribución, tomando el eje de abscisas como referencia) y moda (valor que presenta una ordenada más alta).
Por consiguiente, la posición relativa de los parámetros de centralización pueden servir como una primera medida de la simetría de una distribución.
Otras medidas más precisas son el coeficiente de asimetría de Fisher, el coeficiente de asimetría de Bowley y el coeficiente de asimetría de Pearson.
Medidas de apuntamiento o curtosis
[editar]
Con estos parámetros se pretende medir cómo se reparten las frecuencias relativas de los datos entre el centro y los extremos, tomando como comparación la campana de Gauss.
El parámetro usado con más frecuencia para esta medida es el coeficiente de curtosis de Fisher, definido como:
- ,
aunque hay otros como el coeficiente de curtosis de Kelley o el coeficiente de curtosis percentílico.
La comparación con la distribución normal permite hablar de distribuciones platicúrticas o más aplastadas que la normal; distribuciones mesocúrticas, con igual apuntamiento que la normal; y distribuciones leptocúrticas, esto es, más apuntadas que la normal.[30]
Por último, existen otras medidas para decidir sobre la forma de una distribución con ajuste a modelos menos usuales como los que se muestran en las siguientes gráficas:
Otros parámetros
[editar]Se presentan en este apartado otros parámetros que tienen aplicación en situaciones muy concretas, por lo que no se incluyen entre los grupos anteriores, aunque tienen cabida en este artículo por su frecuente uso en medios de comunicación y su facultad de resumir grandes cantidades de datos, como ocurre con las medidas tratadas hasta ahora.
Proporción
[editar]La proporción de un dato estadístico es el número de veces que se presenta ese dato respecto al total de datos. Se conoce también como frecuencia relativa y es uno de los parámetros de cálculo más sencillo. Tiene la ventaja de que puede calcularse para variables cualitativas.
Por ejemplo, si se estudia el color de ojos de un grupo de 20 personas, donde 7 de ellas los tienen azules, la proporción de individuos con ojos azules es del 35 % (= 7/20).
El dato con mayor proporción se conoce como moda (véase, más arriba).
En inferencia estadística existen intervalos de confianza para la estimación de este parámetro.
Número índice
[editar]Un número índice es una medida estadística que permite estudiar las fluctuaciones o variaciones de una magnitud o de más de una en relación con el tiempo o al espacio. Los índices más habituales son los que realizan las comparaciones en el tiempo. Algunos ejemplos de uso cotidiano de este parámetro son el índice de precios o el IPC[31]
Tasa
[editar]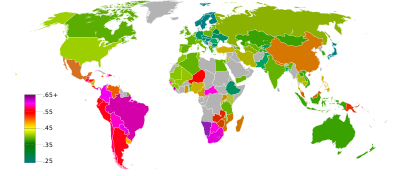
La tasa es un coeficiente que expresa la relación entre la cantidad y la frecuencia de un fenómeno o un grupo de fenómenos. Se utiliza para indicar la presencia de una situación que no puede ser medida en forma directa.[31] Esta razón se utiliza en ámbitos variados, como la demografía o la economía, donde se hace referencia a la tasa de interés.
Algunos de los más usados son: tasa de natalidad, tasa de mortalidad, tasa de crecimiento demográfico, tasa de fertilidad o tasa de desempleo.
Coeficiente de Gini
[editar]El índice de Gini o coeficiente de Gini es un parámetro de dispersión usado para medir desigualdades entre los datos de una variable o la mayor o menor concentración de los mismos.
Este coeficiente mide de qué forma está distribuida la suma total de los valores de la variable. Se suele usar para describir salarios. Los casos extremos de concentración serían aquel en los que una sola persona acapara el total del dinero disponible para salarios y aquel en el que este total está igualmente repartido entre todos los asalariados.[32]
Momentos
[editar]Los momentos son una forma de generalizar toda la teoría relativa a los parámetros estadísticos y guardan relación con una buena parte de ellos. Dada una distribución de datos estadísticos , se define el momento central o momento centrado de orden como
Para variables continuas la definición cambia sumas discretas por integrales (suma continua), aunque la definición es, esencialmente, la misma.[33] De esta definición y las propiedades de los parámetros implicados que se han visto más arriba, se deduce inmediatamente que:
y que
[34]
Se llama momento no centrado de orden k a la siguiente expresión:
De la definición se deduce que:
Usando el binomio de Newton, puede obtenerse la siguiente relación entre los momentos centrados y no centrados:
Los momentos de una distribución estadística la caracterizan unívocamente.[35]
Parámetros bidimensionales
[editar]En estadística se estudian en ocasiones varias características de una población para compararlas, estudiar su dependencia o correlación o realizar cualquier otro estudio conjunto. El caso más común de dos variables se conoce como estadística bidimensional.[36]
Un ejemplo típico es el de un estudio que recoja la estatura (denotada por ) y el peso (denotada por ) de los individuos de una determinada población. En tal caso, fruto de la recogida de datos, se obtendría una serie de parejas de datos , con , cada una de las cuales estaría compuesta por la estatura y el peso del individuo , respectivamente.
En los estudios bidimensionales, cada una de las dos variables que entran en juego, estudiadas individualmente, pueden resumirse mediante los parámetros que se han visto hasta ahora. Así, tendría sentido hablar de la media de las estaturas () o la desviación típica de los pesos (). Incluso para un determinado valor de la primera variable, , cabe hacer estudios condicionados. Por ejemplo, la mediana condicionada a la estatura sería la mediana de los pesos de todos los individuos que tienen esa estatura. Se denota .
Sin embargo existen otros parámetros que resumen características de ambas distribuciones en su conjunto. Los más destacados son el centro de gravedad, la covarianza y el coeficiente de correlación lineal.
Centro de gravedad
[editar]Dadas dos variables estadísticas e , se define el centro de gravedad como la pareja (, ), donde y son, respectivamente, las medias aritméticas de las variables e .
El nombre de este parámetro proviene de que en una representación de las parejas del estudio en una nube de puntos, en la que cada punto tuviese un peso proporcional a su frecuencia absoluta, las coordenadas (, ) corresponderían, precisamente, al centro de gravedad como concepto físico.[37]
Covarianza
[editar]La covarianza o varianza conjunta de una distribución bidimensional se define como:
La interpretación de este parámetro tiene que ver con la eventual correlación lineal de las dos variables. Una covarianza positiva implica una correlación directa y una negativa, una correlación inversa.[38] Por otra parte, es un parámetro imprescindible para el cálculo del coeficiente de correlación lineal o los coeficientes de regresión, como se verá más abajo.
En su contra tiene que se ve excesivamente influenciada, al igual que ocurría con la media aritmética, por los valores extremos de las distribuciones y los cambios de escala.
Coeficiente de correlación lineal
[editar]
Se trata de un coeficiente que permite determinar la bondad del ajuste de la nube de puntos por una recta.
Se define como: , donde es la covarianza y y , las desviaciones típicas respectivas de las distribuciones implicadas.
El coeficiente de correlación lineal toma valores entre −1 y 1. En esa escala, mide la correlación del siguiente modo:
- La correlación lineal es más fuerte cuanto más cerca esté de −1 o 1.
- La correlación lineal es más débil cuanto más próximo a cero sea .[39]
El diagrama de la derecha ilustra cómo puede variar en función de la nube de puntos asociada:
Otros parámetros bidimensionales son, el coeficiente de correlación de Spearman, los coeficientes de correlación no paramétricos, el coeficiente de determinación o los coeficientes de regresión lineal.
Al igual que con distribuciones unidimensionales, existe una forma equivalente de desarrollar la teoría relativa a los parámetros estadísticos bidimensionales usando los momentos.
Los parámetros en la inferencia estadística
[editar]En ocasiones los parámetros de una determinada población no pueden conocerse con certeza. Generalmente esto ocurre porque es imposible el estudio de la población completa por cuestiones como que el proceso sea destructivo (p.e., vida media de una bombilla) o muy caro (p.e., audiencias de televisión). En tales situaciones se recurre a las técnicas de la inferencia estadística para realizar estimaciones de tales parámetros a partir de los valores obtenidos de una muestra de la población.[40]
Se distingue entonces entre parámetros y estadísticos. Mientras que un parámetro es una función de los datos de la población, el estadístico lo es de los datos de una muestra. De este modo pueden definirse la media muestral, la varianza muestral o cualquier otro párametro de los vistos más arriba.
Por ejemplo, dada una muestra estadística de tamaño , , de una variable aleatoria con distribución de probabilidad , donde θ es un conjunto de parámetros de la distribución, se definiría la media muestral -ésima como:
En el caso concreto de la varianza muestral, suele tomarse, por sus mejores propiedades como estimador, la siguiente:
...donde se ha tomado como denominador , en lugar de . A este parámetro también se le llama cuasivarianza.[41]
Controversias y malas interpretaciones
[editar]Como se ha dicho, los parámetros estadísticos, en el enfoque descriptivo que aquí se adopta, substituyen grandes cantidades de datos por unos pocos valores extraídos de aquellos a través de operaciones simples. Durante este proceso se pierde parte de la información ofrecida originalmente por todos los datos. Es por esta pérdida de datos por lo que la estadística ha sido tildada en ocasiones de una falacia. Por ejemplo, si en un grupo de tres personas una de ellas ingiere tres helados, el parámetro que con más frecuencia se utiliza para resumir datos estadísticos, la media aritmética del número de helados ingeridos por el grupo sería igual a uno , valor que no parece resumir fielmente la información. Ninguna de las personas se sentiría identificada con la frase resumen: «He ingerido un helado de media».[21]
Un ejemplo menos conocido pero igual de ilustrativo acerca de la claridad de un parámetro es la distribución exponencial, que suele regir los tiempos medios entre determinados tipos de sucesos. Por ejemplo, si la vida media de una bombilla es de 8000 horas, más del 50 por ciento de las veces no llegará a esa media. Igualmente, si un autobús pasa cada diez minutos de media, hay una probabilidad mayor del 50 por ciento de que pase menos de diez minutos entre un autobús y el siguiente.
Otro ejemplo que suele ofrecerse con frecuencia para argumentar en contra de la estadística y sus parámetros es que, estadísticamente hablando, la temperatura media de una persona con los pies en un horno y la cabeza en una nevera es ideal.

Quizás por situaciones como éstas, que en general muestran un profundo desconocimiento de lo que los parámetros representan en realidad y de su uso conjunto con otras medidas de centralización o dispersión, el primer ministro británico Benjamín Disraeli sentenció[42] primero y Mark Twain popularizó más tarde[43] la siguiente afirmación:
Hay mentiras, grandes mentiras, y estadísticas.
Hay otros personajes que también han advertido sobre la simplificación que supone la estadística, como el profesor Aaron Levenstein, quien afirmaba:
Las estadísticas son como los bikinis: lo que muestran es sugerente, pero lo que esconden es vital.
Por su parte, el escritor y comediante inglés Bernard Shaw sentenció:[44]
La estadística es una ciencia que demuestra que, si mi vecino tiene dos coches y yo ninguno, los dos tenemos uno.
o el personaje ficticio Homer Simpson, de la popular serie de televisión Los Simpson, en una entrevista acerca de las proporciones en uno de sus capítulos:[45]
¡Oh!, la gente sale con estadísticas para probar cualquier cosa, el 14 por ciento del mundo lo sabe.Guionistas de la serie Los Simpson
Véase también
[editar]- Desigualdad de Tchebyschev, teorema que muestra la cantidad de datos que resumen conjuntamente la media aritmética y la desviación típica.
- Diagrama de caja, gráfico en el que se aprecian visualmente las características de algunos de los parámetros de centralización, posición y dispersión.
- Dispersión (matemática).
- Estadística descriptiva, la teoría estadística relativa a los parámetros, tal y como se han expuesto en este artículo, pertenece a esta especialidad matemática.
- Estadística robusta.
- Estadístico, concepto equivalente al de parámetro cuando se trata de una muestra.
- Estimación de parámetros, diversos métodos para predecir el valor real de determinados parámetros poblacionales cuando éstos no pueden conocerse mediante experiencias.
- Intervalo de confianza, método para estimar el valor aproximado de un parámetro estadístico.
- Parámetro, como objeto matemático.
- Parámetros más comunes:
- Parámetros de centralización:
- Parámetros de dispersión:
- Medidas de posición no central:
- Otros parámetros:
- Parámetros bidimensionales:
- Población, como concepto estadístico.
- Regresión estadística
- Dilución de regresión
- Debabrata Basu
Referencias
[editar]- ↑ Ross, Sheldon M. (2007). «3. Uso de la Estadística para sintetizar conjuntos de datos.». Introducción a la Estadística. trad. Valdés Sánchez, Teófilo. Reverte. p. 69. ISBN 8429150390. Consultado el 5 de abril de 2009.
- ↑ Fernández Gordillo, Juan Carlos (2008). «Parámetros estadísticos». Ditutor, Diccionario de Matemáticas. Consultado el 19 de abril de 2009.
- ↑ Serret Moreno-Gil, Jaime (1998). «4. Parámetros Estadísticos». Procedimientos estadísticos. ESIC. p. 71. ISBN 8473561716. Consultado el 19 de abril de 2009.
- ↑ Pascual, José; Galbiati, José; González, Gladys; Maulén, Mª Angélica; Arancibia, Rodrigo. «Conceptos básicos: Modelo». Exploración de datos: Introducción a la Estadística Descriptiva. Diseñadora: Galbiati, Paola. Instituto de Estadística. Universidad Católica de Valparaíso. Archivado desde el original el 10 de abril de 2009. Consultado el 16 de abril de 2009.
- ↑ «Parámetro estadístico». Enciclopedia Microsoft® Encarta® Online 2009. Microsoft Corporation. 2009. Archivado desde el original el 1 de abril de 2009. Consultado el 19 de abril de 2009. «Parámetro estadístico, número que se obtiene a partir de los datos de una distribución estadística y que sirve para sintetizar alguna característica relevante de la misma.»
- ↑ Clapham, Christopher (septiembre de 1998). Diccionario de Matemáticas. Traducción: De Sá Madariaga, Juan Mª L (Primera edición). Oxford-Complutense. p. 266. ISBN 84-89784-56-6. «Parámetro (en estadística): Cierta cantidad que caracteriza de alguna forma a la población, como su media o su mediana».
- ↑ Serret Moreno-Gil, Jaime (1998). «4. Parámetros Estadísticos». Procedimientos estadísticos. ESIC. p. 71. ISBN 8473561716. Consultado el 19 de abril de 2009. «En estadística descriptiva tenemos una serie de expresiones (...) que permiten disponer de unos valores numéricos que reflejan el comportamiento global del suceso estadístico, calculados a partir de los datos individuales. Estas expresiones son los parámetros estadísticos».
- ↑ citado por Calot (1985, pp. 55, 56) y MAD-Eduforma (2006, p. 160)
- ↑ Romero Villafranca, Rafael; Zúnica Ramajo, Luisa Rosa (2005). «2.6. Parámetros de posición». Métodos estadísticos en Ingeniería. Valencia: Univ. Politéc. Valencia. pp. 39-41. ISBN 8497057279. Consultado el 20 de abril de 2009.
- ↑ «Medidas de Dispersión». Enciclopedia Microsoft® Encarta® Online. Microsoft Corporation. 2009. Archivado desde el original el 28 de noviembre de 2015. Consultado el 20 de abril de 2009.
- ↑ Serret Moreno-Gil, Jaime (1998). «4.3. Parámetros de forma.». Procedimientos estadísticos. ESIC. p. 81. ISBN 8473561716. Consultado el 20 de abril de 2009.
- ↑ Wackerly, Dennis D; Mendenhall, William; Scheaffer, Richard L. (2002). «1.3. Descripción de un conjunto de mediciones: métodos numéricos». Estadística matemática con aplicaciones (6ª edición). Cengage Learning Editores. p. 8. ISBN 9706861947. «La medida central que más se usa en estadística es la media aritmética».
- ↑ Rius Díaz, Francisca (octubre de 1997). «2.3.2 La media». Bioestadística. Métodos y aplicaciones. Málaga: Universidad de Málaga. ISBN 84-7496-653-1. Archivado desde el original el 23 de diciembre de 2009. Consultado el 7 de abril de 2009.
- ↑ Wackerly, Dennis D; Mendenhall, William; Scheaffer, Richard L. (2002). «1.3. Descripción de un conjunto de mediciones: métodos numéricos». Estadística matemática con aplicaciones (6ª edición). Cengage Learning Editores. p. 8. ISBN 9706861947. «Dos conjuntos de mediciones podrían tener distribuciones de frecuencias muy distintas, pero con la misma media».
- ↑ Rius Díaz, Francisca. «2.3.6 La moda». Bioestadística. Métodos y aplicaciones. Archivado desde el original
|urlarchivo=requiere|url=(ayuda) el 23 de diciembre de 2009. Consultado el 17 de abril de 2009. - ↑ Santos, María José (abril de 2009). «Retrato robot del alcalde metropolitano». El Correo de Andalucía. Consultado el 7 de abril de 2009.
- ↑ Serret Moreno-Gil, Jaime (1998). Procedimientos estadísticos. ESIC. p. 75. ISBN 8473561716. Consultado el 17 de abril de 2009.
- ↑ Rius Díaz, Francisca. «2.3.4 La mediana». Bioestadística. Métodos y aplicaciones. Archivado desde el original
|urlarchivo=requiere|url=(ayuda) el 23 de diciembre de 2009. Consultado el 17 de abril de 2009. - ↑ Martín Andrés, Antonio; Luna del Castillo, Juan de Dios (2004). Bioestadística para las ciencias de la Salud. Capitel Editores. p. 28. ISBN 8484510182. Consultado el 17 de abril de 2009.
- ↑ Chaves, Bernardo (2004). «La media geométrica y la media armónica». Bioestadística para postgrado. Universidad Nacional de Colombia. Consultado el 7 de abril de 2009. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- ↑ a b Huff, Darrel (1965). «2. El promedio bien escogido». Cómo mentir con estadísticas. Acapulco: Sagitario.
- ↑ Johnson, Robert; Kuby, Patricia (2003). «2.8. El arte del engaño estadístico». Estadística elemental (3ª edición). Cengage Learning Editores. p. 94. ISBN 9706862870.
- ↑ a b Rius Díaz, Francisca. «2.7. Medidas de variabilidad o dispersión». Bioestadística. Métodos y aplicaciones. Archivado desde el original
|urlarchivo=requiere|url=(ayuda) el 23 de diciembre de 2009. Consultado el 17 de abril de 2009. - ↑ Férnandez Fernández, Santiago; Alejandro Córdoba, José María Cordero Sánchez, Alejandro Córdoba (2002). «4.2. Medidas absolutas». Estadística Descriptiva (2ª edición). ESIC Editorial. p. 192. ISBN 8473563069.
- ↑ a b Rius Díaz, Francisca. «2.7.4. Varianza y desviación típica». Bioestadística. Métodos y aplicaciones. Consultado el 7 de abril de 2009.
- ↑ Wackerly, Dennis D. «3.11. Teorema de Chebyshev». Estadística matemática con aplicaciones. p. 139.
- ↑ Férnandez Fernández, Santiago. «4.2.3.4. Meda o desviación mediana». Estadística Descriptiva. p. 200.
- ↑ Férnandez Fernández, Santiago. «4.3. Medidas relativas». Estadística Descriptiva. p. 201.
- ↑ Férnandez Fernández, Santiago. «4.3. Medidas relativas». Estadística Descriptiva. p. 202.
- ↑ Sotomayor Velasco, Gabriel; Wisniewski, Piotr Marian (2001). «8.7. Momentos y otras características». Probabilidad y estadística para ingeniería y ciencias. Cengage Learning Editores. p. 196. ISBN 970686136X. Consultado el 7 de abril de 2009.
- ↑ a b Malléa, Adriana, Adriana; Herrera, Myriam; Ruiz, Ana María (2003). «3. Parámetros estadísticos no convencionales». Estadística en el nivel polimodal. San Juan: effha. p. 67. ISBN 9872084920. Consultado el 17 de abril de 2009.
- ↑ Llorente Galera, Francisco; Staff, VV; Marín Feria, Susana; Torra Porras, Salvador (2000). «2.6. Medidas de concentración». Principios de estadística descriptiva aplicada a la empresa. Ramón Areces. pp. 53-54. ISBN 8480044276. Consultado el 17 de abril de 2009. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- ↑ Wackerly, Dennis D. «3.9. Momentos y funciones generadoras de momentos». Estadística matemática con aplicaciones. p. 131.
- ↑ «Estadísticos de tendencia central». Archivado desde el original el 23 de diciembre de 2009.
- ↑ Casas Sánchez, J.M; Santos Peña, Julián (2002). «2.6. Momentos». Introducción a la estadística para economía (2 edición). Ramón Areces. p. 95. ISBN 848004523X. «Si los momentos coinciden en dos distribuciones, diremos que son iguales». (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- ↑ Cáceres Hernández, Juan José (2007). «4.1. Variable estadística multidimensional y distribución de frecuencias». Conceptos básicos de Estadística para Ciencias Sociales. Delta Publicaciones. p. 62. ISBN 8496477436.
- ↑ Arias Rodríguez, Jose Carlos (2004). «Distribuciones bidimensionales». Proyecto Descartes. Madrid: Ministerio de Educación, Política Social y Deporte. Consultado el 7 de abril de 2009.
- ↑ Rius Díaz, Francisca (octubre de 1997). «3.10.2. Una interpretación geométrica de la covarianza». Bioestadística. Métodos y aplicaciones. Málaga: Universidad de Málaga. ISBN 84-7496-653-1. Archivado desde el original el 23 de diciembre de 2009. Consultado el 7 de abril de 2009.
- ↑ Barón López, Francisco Javier. «Bioestadística» (Vídeo en Flash). Málaga: Universidad de Málaga. Consultado el 18 de abril de 2009.
- ↑ Casas Sánchez, Jose M.; Manzano Arrondo, Vicente; Zamora Sanz, Ana Isabel (1997). «2. Estimación puntual». Inferencia Estadística (2ª, ilustrada edición). Ramón Areces. pp. 89-162. ISBN 848004263X. Consultado el 17 de abril de 2009. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- ↑ Álvarez Leiva, Juan Antonio (diciembre de 1997). «Medidas de dispersión». Proyecto CICA Thales. Sociedad Andaluza de Educación Matemática «Thales». Archivado desde el original el 8 de abril de 2009. Consultado el 7 de abril de 2009.
- ↑ «Citas de Benjamin Disraeli en Wikiquote». Consultado el 5 de abril de 2009.
- ↑ «Mentiras, grandes mentiras y estadísticas en la Wikipedia inglesa»
|url=incorrecta con autorreferencia (ayuda). - ↑ Citas de Bernard Shaw
- ↑ Los Simpsons, temporada 5 Archivado el 3 de mayo de 2020 en Wayback Machine., episodio Homer, el vigilante
Bibliografía
[editar]- Calot, Gérard (1985). Curso de estadística descriptiva. trad. Francisco José Cano Sevilla (4ª edición). Parainfo. ISBN 8428305633.
- Férnandez Fernández, Santiago; Córdoba, Alejandro; Cordero Sánchez, José María (2002). Estadística Descriptiva (2ª edición). ESIC Editorial. ISBN 8473563069.
- Huff, Darrel; Geis, Irvin (1993). How to lie with Statistics. W W Norton & Co Inc. ISBN 0393310728.
- Rius Díaz, Francisca (1997). Bioestadística. Métodos y aplicaciones (2ª edición). Universidad de Málaga. ISBN 84-7496-653-1.
- Velasco Sotomayor, Gabriel; Wisniewski, Piotr Marian (2001). Probabilidad y estadística para ingeniería y ciencias. Cengage Learning Editores. pp. 185-197. ISBN 970686136X.
- Técnicos de Administración Del Ministerio de Economía Y Hacienda (instituto Nacional de Estadística). Grupos III Y IV. Temario Específico Y Test Ebook. MAD-Eduforma. 2006. ISBN 9788466552509.
Enlaces externos
[editar]Calculadoras de parámetros estadísticos:
- Las tres medias Calcula la media aritmética, geométrica y armónica de una serie de 80 datos o menos.
- La calculadora web descriptiva Archivado el 6 de abril de 2009 en Wayback Machine. Calcula media, moda, varianza, desviación típica, coeficiente de variación, coeficientes de forma, índice Gini, media armónica.
- Calculadora estadística Incluye parámetros bidimensionales y otros cálculos de utilidad en probabilidad.
Cursos completos de estadística descriptiva:
- Estadística descriptiva (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).. Hecho con Moodle, por la Universidad de Antioquia.
- Bioestadística, métodos y aplicaciones, por la Universidad de Málaga.
 KSF
KSF












![{\displaystyle [L_{i},L_{s}]=[Q_{1}-1.5\cdot R_{s},Q_{3}+1.5\cdot R_{s}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04aca39aea32b6cc4acbc2a84ae31f2342d742f8)