41 (число)

41
сорок один
← 39 · 40 · 41 · 42 · 43 →
Разложение на множители	41 (простое)
Римская запись	XLI
Двоичное	101001
Восьмеричное	51
Шестнадцатеричное	29
Медиафайлы на Викискладе

41 (сорок один) — натуральное число, расположенное между числами 40 и 42.

Эта статья должна быть полностью переписана. На странице обсуждения могут быть пояснения.

Эта страница требует существенной переработки. Возможно, её необходимо правильно оформить, дополнить или переписать. Пояснение причин и обсуждение — на странице Википедия:К улучшению/9 августа 2022.

• 41 — натуральное, нечётное, двузначное (в десятичной системе счисления) число
• квадрат числа 41 равен 1681
• 2⁴¹ = 2 199 023 255 552
• 1/41 = 0.0243902… (бесконечная десятичная дробь с периодом длины 5)

В этом разделе указаны свойства, связанные с вопросами представления числа 41 как значения некоторых примечательных числовых выражений.

• 5-е центрированное квадратное число, то есть представимо в виде суммы двух последовательных квадратов натуральных чисел (41 = 4² + 5²);

41 = 42 + 52

также представимо в виде суммы трёх квадратов натуральных чисел (41 = 6² + 2² + 1²); при этом 41 является наименьшим числом, представимым в виде суммы квадратов двух натуральных чисел и одновременно в виде суммы квадратов трёх натуральных чисел, где все пять указанных чисел различны

• 41 = 21² — 20², не представимо другими способами в виде разности степеней (от 2) двух натуральных чисел
• 8-е число Прота, 5-е простое число Прота (41 = 5 × 2³ + 1)
• наименьшее натуральное число, не представимое в виде |2^x−3^y|, где x и y — натуральные числа

В этом разделе указаны свойства числа 41, связанные с отношением делимости на множестве натуральных чисел.

• 13-е простое число, близнец простого числа 43, отличается на шесть от простого числа 47
• 6-е пифагорово простое число (имеет вид 4n+1); 2-е (после 17) простое число вида 8n+1
• 7-е натуральное число n такое, что n!+1 простое^[1]
• 5-е сильное простое число
• 11-е регулярное простое число
• 2-е простое число Ньюмена — Шэнкса — Уильямса
• 7-е число Софи Жермен (41 × 2 + 1 = 83, также являющееся простым числом)^[2]. С числа 41 начинается полная последовательность Куннингама 1-го рода длины 3 (41 , 83 , 167)
• сумма первых шести простых чисел: 41 = 2 + 3 + 5 + 7 + 11 + 13; также представимо в виде суммы трёх последовательных простых чисел: 41 = 11 + 13 + 17
• равно сумме всех положительных делителей чисел от 1 до 7: 41 = 1 + 1 + 2 + 1 + 3 + 1 + 2 + 4 + 1 + 5 + 1 + 2 + 3 + 6 + 1 + 7
• присутствует в трёхчлене Эйлера (n² + n + 41), значение которого является простым числом при целых n, по модулю меньших 40
• наименьшее простое число такое, что сумма всех простых чисел, не превосходящих его, раскладывается в произведение трёх различных простых сомножителей (238 = 2 × 7 × 17)
• значения некоторых теоретико-числовых функций:

функции Эйлера: φ (41) = 40;

пи-функции: π (41) = 13;

τ-функции (количество натуральных делителей): τ (41) = 2;

σ-функции (сумма натуральных делителей): σ (41) = 42 (41 — недостаточное число);

функции Мёбиуса: μ (41) = −1;

функции Мертенса: M (41) = −1

Здесь приводятся свойства, касающиеся записи числа 41 в десятичной системе счисления и связанных с ней вопросов (в частности, удобства устных вычислений и проверки делимости).

• десятичная запись числа 41 образована последовательно записанными двумя квадратами (4 и 1); тем же свойством обладает его квадрат 1681 (16 и 81)
• число 99999 делится на 41 (10⁵=100000 даёт остаток 1 при делении на 41). Использование этого свойства помогает решить некоторые задачи олимпиадного типа. Из этого свойства также следует признак делимости на 41: «Натуральное число делится на 41 тогда и только тогда, когда при отделении от его десятичной записи всех групп по пять цифр, начиная с конца, и суммировании всех получившихся натуральных чисел получается число, кратное 41». (Пример: число 864694512870 делится на 41, поскольку 86 + 46945 + 12870 делится на 41.)

Делимость числа 10⁵−1 на 41 имеет несколько важных следствий:

1. 41 делит число 11111, а также любое число вида 10…010…010…010…01, где во всех четырёх группах одинаковое количество нулей, не равное 5k-1 при натуральном k; верно и более сильное утверждение: если любое число, количество знаков в котором не кратно 5, записать в строку пять раз без пробелов, то получится число, кратное 41.
2. Если пятизначное число делится на 41, то при любой круговой перестановке его цифр эта делимость сохраняется (пример: 16359 делится на 41, следовательно, делятся на 41 числа 63591, 35916, 59163 и 91635). Этот факт многократно указывается как интересное свойство числа 41 как математиками^[3][4], так и любителями нумерологии^[5][6].

• Другие признаки делимости числа на 41:
  • число делится на 41 тогда и только тогда, когда модуль разности числа десятков и четырёхкратного числа единиц делится на 41. Например, 369 делится на 41, так как ${\displaystyle \left|36-4\cdot 9\right|=0}$ делится на 41.
  • чтобы проверить, делится ли число на 41, его следует справа налево разбить на грани по 5 цифр в каждой. Затем в каждой грани первую справа цифру умножить на 1, вторую цифру умножить на 10, третью — на 18, четвёртую — на 16, пятую — на 37 и все полученные произведения сложить. Результат будет делиться на 41 тогда и только тогда, когда само число делится на 41^[7].
• 41 есть наименьшее такое число, что минимальное значение суммы цифр кратного ему равно 5^[7]
• 41 равно сумме цифр пятых степеней чисел 29, 56, 83, 92; 41 не равно сумме цифр какого-либо натурального числа в степени 2 или 3 или 4

• 41² = 40² + 9² (41 — 7-е число, являющееся наибольшим в некоторой примитивной пифагоровой тройке^[8])
• 41 — 7-е действительное простое число Эйзенштейна
• среди чисел от 1 до 40 квадратичными вычетами по модулю 41 являются числа 1, 2, 4, 5, 8, 9, 10, 16, 18, 20, 21, 23, 25, 31, 32, 33, 36, 37, 39, 40, квадратичными невычетами — остальные числа

• Атомный номер ниобия

• Дафна — крупный астероид главного пояса, обнаруженный с помощью телескопа в 1856 году парижским астрономом.
• Звёзды 41 Рыси, 41 Рака, 41 Змеи, 41 Жертвенника, HAT-P-41, WASP-41; скопление М41.

Технические объекты:

• SLC-41 (LC-41) — стартовая площадка на мысе Канаверал (США), с которой в течение долгого времени осуществляются запуски космических аппаратов важнейших научных миссий, в том числе Викинг-1 и Викинг-2 (исследования Марса), Mars Science Laboratory (доставка марсохода Кьюриосити на Марс), Вояджер-1 (исследование Юпитера и Сатурна, определение границ Солнечной системы), Вояджер-2 (исследование Урана и Нептуна, определение границ Солнечной системы), Новые горизонты (исследования Плутона, Харона).
• Площадка № 41 космодрома Байконур (Казахстан, ранее СССР) известна в связи с одной из крупнейших катастроф в истории космических полётов.
• На 2014 год для исследования планеты Марс был запущен 41 космический аппарат.

• 41 °C — средняя температура тела у ряда животных (прежде всего птиц)^[9]. У человека такая температура возможна при серьёзной болезни и считается опасным признаком^[10].

Значимость числа 41 в религии и мифологии (легендах, мифах, обрядах) в большой степени связана с фундаментальным значением предшествующего натурального числа 40, которое многократно встречается во всех наиболее распространённых религиях (например, несколько раз в библейском повествованию о Всемирном потопе, описании жизни пророка Мухаммеда и т. д.).

В календаре инков, по утверждениям некоторых хронистов, использовался цикл, состоящий из 328 дней, состоящий из 41 недели по 8 дней^[11].

У марийцев число 41 играет важную роль во многих обрядах:

• При свадьбе молодожёны должны наступить на 41 зло и принять 41 доброту;
• При похоронах в гроб к усопшему кладут котомку, в которой находится 41 орех^[12], а замещающее усопшего лицо отходит от определённого места на 41 шаг;
• В ходе праздника Семык во время ритуального похода в баню полагается похлестать своё тело веником, связанным из 41 вида растений.

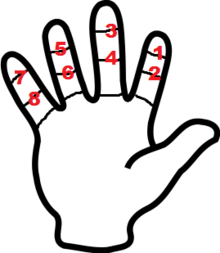
В средневековой Руси был широко распространён пальцевый счёт «сороковицами»: по суставам пальцев от одного до сорока. Такой способ счёта означает фактическое использование 40-ичной системы счисления, в которой 40 является самой большой цифрой, а 41 — первым двузначным числом. В связи с этим число 40 ассоциировалось с понятием конца счёта, фактически принимая значение «много», что широко отражено в русском языке и русской литературе (см. 40 (число), Сороковины, Сорок сороков)^[13]. С этим связаны некоторые древние представления о числе 41 как неблагоприятном.

• Согласно сибирскому поверью, если охотник убил сорок медведей, то от сорок первого погибнет сам^[13] (по другой версии, роковым становится сороковой медведь^[14][15]). С этим, в частности, связаны строки поэта Некрасова:

Ведь наскочил же на экую гадину!
Сын ли мой не был удал?
Сорок медведей поддел на рогатину —
На сорок первом сплошал!

— «В деревне»

• повесть Бориса Лавренёва «Сорок первый»
• песня Михаила Анчарова «Сорок первый»^[16]
• рассказ Альберта Воронина «Сорок первый»^[17]

У чувашей 41 — одно из сакральных чисел, используется в некоторых обрядах^[18].

• В 41 год Публий Элий Адриан стал римским императором, сменив императора Траяна (117 год н. э.).
• 41 государство включал Германский союз в 1815 году (год образования союза).
• 41-й км Ленинградского шоссе (Россия, Московская область) — самое близкое к Москве точно подтверждённое место наступления войск Вермахта в 1941 году (с этого рубежа началось контрнаступление советских войск на Ленинградском направлении)^[19].
• В годы Второй мировой войны действовали следующие военные формирования с порядковым номером 41: 41-й истребительный авиационный полк, 41-й моторизованный корпус, 41-й отдельный лыжный батальон, 41-й отдельный моторизованный понтонно-мостовой батальон, 41-й отдельный танковый батальон, 41-й стрелковый корпус, 41-й танковый корпус, 41-я авиационная дивизия, 41-я армия, 41-я стрелковая дивизия (1-го формирования), 41-я стрелковая дивизия (2-го формирования), 41-я кавалерийская дивизия, 41-я танковая дивизия.
• «41 за свободу» — неофициальное название группы стратегических атомных подводных лодок «Поларис», построенных США в 1958—1967 гг. и позже заменённых. Лодки получили названия в честь известных деятелей США. Данное количество было ограничено советско-американским договором ОСВ-1 1972 года. Эти лодки стали главным противником СССР в годы Холодной войны.
• Джордж Буш — 41-й президент США.

• 41 дисциплина входит в летние олимпийские виды спорта
• На 41-й Генеральной ассамблее Европейского Олимпийского комитета принято решение о проведении первых в истории Европейских игр

• 41 безответный гол забила команда «Динамо» (Москва) в ворота «Локомотива» (Оренбург) в чемпионате России по хоккею с мячом 28 декабря 2006 года. Матч завершился со счётом 41:0.

• «Сорок первый» — повесть писателя Бориса Лавренёва (1924 год, экранизирована в 1927 и 1956 годах) о любви красного стрелка Марютки и белогвардейского поручика во времена Гражданской войны^[20]
• рассказ «№ 41»^[21]

• Сорок один жеребёнок, марийская сказка
• Сорок одна небылица, марийская сказка
• Мальчик-богатырь, марийская сказка

• О сорока плешивых и одном косом, крымско-татарская сказка
• 41-й сонет Шекспира^[22]

Фильмы:

• Сорок первый (фильм, 1927), Сорок первый (фильм, 1956) — фильмы по книге Бориса Лавренёва
• В июне 41-го (Россия, 2008), Весна сорок первого (Польша, 2008), Сорок первый год: Противостояние, Яблоки сорок первого года, также многие документальные фильмы — о Второй мировой войне (год 1941).
• 0-41* — индийский документальный драматический фильм режиссёра Сенна Хегде.

• 41 год, 141 год, 241 год, 341 год, 441 год, 541 год, 641 год, 741 год, 841 год, 941 год, 1041 год, 1141 год, 1241 год, 1341 год, 1441 год, 1541 год, 1641 год, 1741 год, 1841 год, 1941 год, 2041 год
• 41 год до н. э.
• 41-й день в году — 10 февраля

• ASCII-код символа «)»
• Телефонный код Швейцарии +41
• Монтана — 41-й штат США
• Луар и Шер — 41-й департамент во Франции
• В России 41 — код Камчатского края
• Телеканал Студия-41
• Sum 41 — канадская панк-группа
• Процесс C-41 — процесс обработки фотоплёнки
• «Сорок один» — окружная газета Зеленограда
• «Сорок одно» — карточная игра
• 41° («сорок первый градус») — группа поэтов в Тифлисе в начале двадцатого века
• ровно 41 буква присутствует в алфавите тофаларского языка, в кириллическом варианте каракалпакского алфавита
• Автодороги Р41 (в Белоруссии), М41 (в Средней Азии), шоссе 41 (в Израиле)
• География: 41-й меридиан восточной долготы (на датском языке: 41. østlige længdekreds), 41-й меридиан западной долготы
• Железная дорога: 41 км (платформа), Площадка 41 км
• Симфония № 41 (Моцарт)

• David Wells. The Penguin Dictionary of Curious and Interesting Numbers