Kinetic Energy

Kinetic energy represents the energy associated with the motion of an object.^[1] It is defined as the work done by a force to accelerate that object from rest to some speed , in the absence of any other forces acting upon the object. Kinetic energy is a scalar and has the same units as work (i.e. Joule).

Classical mechanics[edit]

Translational kinetic energy[edit]

In classical mechanics, the translational kinetic energy of a ridid object, , can be found as:

Where

is the mass of the object

is the velocity of the object

Rotational kinetic energy[edit]

The rotational kinetic energy of a rigid object is:

Where

is the moment of inertia of the object

is the angular velocity of the object

Work-Energy theorem[edit]

The change of kinetic energy is equal to the total work done on it by the resultant of all forces acting on it. For a point mass this can be expressed as:

Where

is the initial speed

is the final speed

Note that if the mass of an object is increased, the increase in kinetic energy increases linearly; if the velocity of an object is increased, the increase in kinetic energy increases quadratically. For example, doubling the mass of an object doubles its kinetic energy; doubling its velocity quadruples its kinetic energy.

Derivation of translational kinetic energy[edit]

The work done by a force accelerating an object from rest, which is the kinetic energy is:

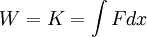
From Newton's second law, the force, , is . Hence we can make the substitution and use the chain rule

This is the same as

In classical mechanics, momentum is given by . Differentiating and substituting into the above equation results in

We want to integrate between 0 and the speed of the object, as this defines kinetic energy. Performing the integration reveals that the kinetic energy is, as expected, the following:

A similar method may be used to derive the formula for rotational kinetic energy.

Kinetic Energy in Relativity[edit]

In relativity, kinetic energy can be expressed as:

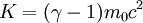
where

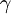is the Lorentz factor

is the rest mass

is the speed of light

This can be shown to be equivalent to the classical equation for kinetic energy, , by performing a binomial expansion on it. Using the result:

Expanding the Lorentz factor in this way, we see:

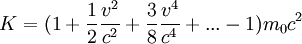
This simplifies to

For speeds encountered everyday, which are a lot less than that of light (such that ), all terms apart from the first are very small and can be neglected. Hence, the formula reduces to:

which is the classical formula.

Derivation[edit]

The kinetic energy is the work done accelerating a particle from rest to some speed . Suppose the particle is at rest at 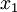and speed at position . Hence:

Since 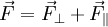, and a perpendicular force does no work, we can ignore the perpendicular component and write:

Since 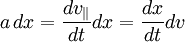, we find the integral can be rewritten as:

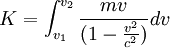
where is the initial speed and hence 0 by definition and is the final speed.

Performing the integration reveals the kinetic energy as:

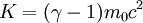
References[edit]

1. ↑ Serway and Beichner, Physics for Scientists and Engineers, Fifth Edition