Black Body

A black body is an hypothetical object that absorbs all light radiation incident upon it. Because light cannot pass through or reflect from a black body, all radiation incident from such an object is emitted from the object itself. Therefore, the idea of a black body is a useful theoretical tool for studying thermal emission apart from other radiative effects. The idea also has great practical use, since though in practice no object is a perfect absorber of light, many real objects (such as the Sun, or a hot filament in a lightbulb) emit so much more radiation than they reflect or transmit that they can be described extremely successfully with a black body model.

Like all light, the light emitted by a black body has a particular energy which depends upon its frequency, or how quickly the light waves oscillate. In the visible spectrum, we see this energy difference as colour - our visual systems are tuned to interpret light of a certain frequency as red, of a different frequency as blue, etc. There is also an infinite range of frequencies that are too high or too low for us to see, although they still transmit energy. For instance, radio waves are very low frequency light, while X-rays have very high frequencies. Black bodies emit a characteristic range of these frequencies, whose exact shape depends on the black body's temperature. This is why objects glow different colours as they are heated - the peak frequency of emission rises with temperature. In fact, all objects, even apparently dark ones, emit light of some frequency. However, most of the objects around us are too cold for their peak frequency to be in the visible range and are instead in the infrared part of the spectrum. This is one of the reasons why infrared goggles make it possible to see in the dark: the goggles pick up the low-energy "glow" of room-temperature objects.

The characteristic range of frequencies, or "frequency spectrum", emitted by a black body can be experimentally measured by heating a black body up to a known temperature, then measuring the intensity ("brightness") of the energy that the black body emits at each frequency. The means to do this were available to late 19th century physicists, and thus the shape of this curve was known then. However, these physicists could not calculate the shape of this curve from theory. This is because an important result in classical mechanics called the "equipartition theorem" states that, on average, the energy of a large group of objects must be evenly distributed between all the different ways that those objects can store energy. For example, a system of thousands of pendulums hanging from rubber bands would, on average, spend half of its kinetic energy on the swinging of the pendulums, and the other half on the bouncing of the rubber bands. If the pendulums were also able to rotate, then the energy would be divided evenly three ways between swinging, bouncing, and rotation.

The application of this result to black body radiation implies that the energy of a black body should be evenly distributed between all the different frequencies of light the black body can emit. However, another result from classical electrodynamics implies that higher frequencies of light can store energy in more ways than lower ones. Since there is no maximum frequency of light, this means that the number of ways a black body can store energy increases without limit for higher frequencies. Since the equipartition theorem says the object's energy must be distributed evenly between all of these ways, more and more energy must go into higher and higher frequencies. Most ways to oscillate would therefore be at high frequencies, which would mean that high-frequency light should always dominate. In fact, the amount of emitted light diverges to infinity as frequency increases - classical physics makes the obviously wrong prediction that all objects should emit infinite amounts of hard radiation.

Albert Einstein was able to correctly model the observed spectrum of blackbody radiation using an earlier result of Max Planck's. Planck postulated that light energy could not be emitted continuously as classical physics predicts, but instead could only come in independent bundles called light quanta, or photons. These photons would have an energy equal to the frequency multiplied by a small factor 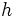, now called Planck's constant. The total emitted energy is equal to the sum of the energies of the photons. As the energies of the individual photons get higher, less different combinations of photons exist that sum up to the total energy. Thus, Planck's assumption makes the radiation of extremely high-energy photons very improbable, and the most probable combination of photons turns out to be that experimentally observed. This is one of the earliest successes of quantum mechanics.