Von Neumann Neighborhood
 From Handwiki
From Handwiki 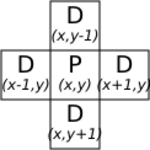
In cellular automata, the von Neumann neighborhood (or 4-neighborhood) is classically defined on a two-dimensional square lattice and is composed of a central cell and its four adjacent cells.[1] The neighborhood is named after John von Neumann, who used it to define the von Neumann cellular automaton and the von Neumann universal constructor within it.[2] It is one of the two most commonly used neighborhood types for two-dimensional cellular automata, the other one being the Moore neighborhood.
This neighbourhood can be used to define the notion of 4-connected pixels in computer graphics.[3]
The von Neumann neighbourhood of a cell is the cell itself and the cells at a Manhattan distance of 1.
The concept can be extended to higher dimensions, for example forming a 6-cell octahedral neighborhood for a cubic cellular automaton in three dimensions.[4]
Von Neumann neighborhood of range r
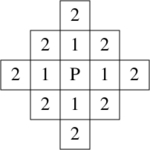
An extension of the simple von Neumann neighborhood described above is to take the set of points at a Manhattan distance of r > 1. This results in a diamond-shaped region (shown for r = 2 in the illustration). These are called von Neumann neighborhoods of range or extent r. The number of cells in a 2-dimensional von Neumann neighborhood of range r can be expressed as [math]\displaystyle{ r^2 + (r+1)^2 }[/math]. The number of cells in a d-dimensional von Neumann neighborhood of range r is the Delannoy number D(d,r).[4] The number of cells on a surface of a d-dimensional von Neumann neighborhood of range r is the Zaitsev number (sequence A266213 in the OEIS).
See also
- Moore neighborhood
- Neighbourhood (graph theory)
- Taxicab geometry
- Lattice graph
- Pixel connectivity
- Chain code
References
- ↑ Toffoli, Tommaso; Margolus, Norman (1987), Cellular Automata Machines: A New Environment for Modeling, MIT Press, p. 60.
- ↑ Ben-Menahem, Ari (2009), Historical Encyclopedia of Natural and Mathematical Sciences, Volume 1, Springer, p. 4632, ISBN 9783540688310, https://books.google.com/books?id=9tUrarQYhKMC&pg=PA4632.
- ↑ Wilson, Joseph N.; Ritter, Gerhard X. (2000), Handbook of Computer Vision Algorithms in Image Algebra (2nd ed.), CRC Press, p. 177, ISBN 9781420042382, https://books.google.com/books?id=YBlSUIybptwC&pg=PA177.
- ↑ 4.0 4.1 Breukelaar, R.; Bäck, Th. (2005), "Using a Genetic Algorithm to Evolve Behavior in Multi Dimensional Cellular Automata: Emergence of Behavior", Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation (GECCO '05), New York, NY, USA: ACM, pp. 107–114, doi:10.1145/1068009.1068024, ISBN 1-59593-010-8.
External links
- Weisstein, Eric W.. "von Neumann Neighborhood". http://mathworld.wolfram.com/vonNeumannNeighborhood.html.
- Tyler, Tim, The von Neumann neighborhood at cell-auto.com
 |
Categories: [Cellular automata]
↧ Download as ZWI file | Last modified: 08/13/2024 10:53:24 | 7 views
☰ Source: https://handwiki.org/wiki/Von_Neumann_neighborhood | License: CC BY-SA 3.0

 KSF
KSF