Book (Graph Theory)

A triangular book

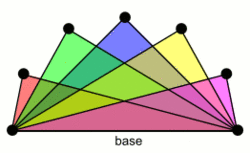
In graph theory, a book graph (often written [math]\displaystyle{ B_p }[/math] ) may be any of several kinds of graph formed by multiple cycles sharing an edge.

Variations

One kind, which may be called a quadrilateral book, consists of p quadrilaterals sharing a common edge (known as the "spine" or "base" of the book). That is, it is a Cartesian product of a star and a single edge.^[1][2] The 7-page book graph of this type provides an example of a graph with no harmonious labeling.^[2]

A second type, which might be called a triangular book, is the complete tripartite graph K_1,1,p. It is a graph consisting of [math]\displaystyle{ p }[/math] triangles sharing a common edge.^[3] A book of this type is a split graph. This graph has also been called a [math]\displaystyle{ K_e(2,p) }[/math]^[4] or a thagomizer graph (after thagomizers, the spiked tails of stegosaurian dinosaurs, because of their pointy appearance in certain drawings) and their graphic matroids have been called thagomizer matroids.^[5] Triangular books form one of the key building blocks of line perfect graphs.^[6]

The term "book-graph" has been employed for other uses. Barioli^[7] used it to mean a graph composed of a number of arbitrary subgraphs having two vertices in common. (Barioli did not write [math]\displaystyle{ B_p }[/math] for his book-graph.)

Within larger graphs

Given a graph [math]\displaystyle{ G }[/math], one may write [math]\displaystyle{ bk(G) }[/math] for the largest book (of the kind being considered) contained within [math]\displaystyle{ G }[/math].

Theorems on books

Denote the Ramsey number of two triangular books by [math]\displaystyle{ r(B_p,\ B_q). }[/math] This is the smallest number [math]\displaystyle{ r }[/math] such that for every [math]\displaystyle{ r }[/math]-vertex graph, either the graph itself contains [math]\displaystyle{ B_p }[/math] as a subgraph, or its complement graph contains [math]\displaystyle{ B_q }[/math] as a subgraph.

• If [math]\displaystyle{ 1\leq p\leq q }[/math], then [math]\displaystyle{ r(B_p,\ B_q)=2q+3 }[/math].^[8]
• There exists a constant [math]\displaystyle{ c=o(1) }[/math] such that [math]\displaystyle{ r(B_p,\ B_q)=2q+3 }[/math] whenever [math]\displaystyle{ q\geq cp }[/math].
• If [math]\displaystyle{ p\leq q/6+o(q) }[/math], and [math]\displaystyle{ q }[/math] is large, the Ramsey number is given by [math]\displaystyle{ 2q+3 }[/math].
• Let [math]\displaystyle{ C }[/math] be a constant, and [math]\displaystyle{ k = Cn }[/math]. Then every graph on [math]\displaystyle{ n }[/math] vertices and [math]\displaystyle{ m }[/math] edges contains a (triangular) [math]\displaystyle{ B_k }[/math].^[9]

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Book (graph theory). Read more