Quantum Number

Quantum numbers are sets of parameters that produce physically acceptable solutions to the Schrodinger equation. They often take integer or half-integer values. They are used to label the different eigenstates of a quantum system. The number of quantum numbers in a system depends on the system, but there will be equal to or greater than the number of dimensions in the problem.

Infinite Square well[edit]

The problem of an infinite square well demonstrates quantum numbers. For a one dimensional box, the possible eigenstates (states in which the we might find the system in when we make a measurement of it) are:

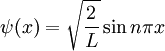
Here, 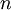is our quantum number and can take integer values. Notice how in this 1 dimensional problem there is only 1 quantum number. The infinite square well problem can be extended to consider a particle trapped inside a 3 dimensional box. This produces a solution of the form:

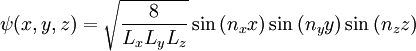
where 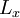, 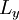and 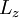are the lengths of each side of the box. Now that we are working in three dimensions, the number of quantum numbers has increased to 3. They are: 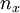, , 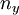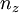and again take integer values.

The Hydrogen Atom[edit]

Four quantum numbers are required to describe the state of an electron in a hydrogen atom. As the electron is a fermion, the Pauli exclusion principle applies and states that no electron can have the same four quantum numbers. The four quantum numbers are:

Principle quantum number - corresponds to the main electron shell in which the electron resides. Can have the value n=1, 2, 3..., corresponding to shells with increasing amounts of energy. However, in stable atoms, this tends to be less than or equal to 7
Azimuthal quantum number - corresponds to the electron subshell of the electron. Can have the number l=0, 1, 2, 3 up to n-1. It is also sometimes called the "angular momentum quantum number", due to its relationship with angular momentum
Magnetic quantum number - corresponds to the orbital of the electron, the orbital is the different orientations of the electron subshell around the atom. It is normally denoted by m and varies from -l to l, taking integer values, i.e. -l, -l + 1,..., -1, 0, 1, ..., l-1, l
Spin quantum number - corresponds to the spin of the electron, can have the value 1/2 or -1/2, indicating that each orbital of an atom can only hold 2 electrons. This is an example of a quantum number that takes half-integer values.

Although this is an example with three dimensions, there are 4 quantum numbers due to spin. Considering the electron as a planet orbiting the proton can be a useful analogy to understand spin. In this analogy, the angular momentum of a planet about the sun corresponds the azimuthal quantum number and the rotation of the planet about its axis to spin. However, the analogy is not perfect; an electron is a point particle and therefore it makes no sense for it to rotate about its own axis. Instead, the electron is said to have an intrinsic angular momentum.

See also[edit]

• Atom