Center (Category Theory)
 From Handwiki
From Handwiki
In category theory, a branch of mathematics, the center (or Drinfeld center, after Soviet-American mathematician Vladimir Drinfeld) is a variant of the notion of the center of a monoid, group, or ring to a category.
Definition
The center of a monoidal category , denoted , is the category whose objects are pairs (A,u) consisting of an object A of and an isomorphism which is natural in satisfying
and
- (this is actually a consequence of the first axiom).[1]
An arrow from (A,u) to (B,v) in consists of an arrow in such that
- .
This definition of the center appears in (Joyal Street). Equivalently, the center may be defined as
i.e., the endofunctors of C which are compatible with the left and right action of C on itself given by the tensor product.
Braiding
The category becomes a braided monoidal category with the tensor product on objects defined as
where , and the obvious braiding.
Higher categorical version
The categorical center is particularly useful in the context of higher categories. This is illustrated by the following example: the center of the (abelian) category of R-modules, for a commutative ring R, is again. The center of a monoidal ∞-category C can be defined, analogously to the above, as
- .
Now, in contrast to the above, the center of the derived category of R-modules (regarded as an ∞-category) is given by the derived category of modules over the cochain complex encoding the Hochschild cohomology, a complex whose degree 0 term is R (as in the abelian situation above), but includes higher terms such as (derived Hom).[2]
The notion of a center in this generality is developed by (Lurie 2017). Extending the above-mentioned braiding on the center of an ordinary monoidal category, the center of a monoidal ∞-category becomes an -monoidal category. More generally, the center of a -monoidal category is an algebra object in -monoidal categories and therefore, by Dunn additivity, an -monoidal category.
Examples
(Hinich 2007) has shown that the Drinfeld center of the category of sheaves on an orbifold X is the category of sheaves on the inertia orbifold of X. For X being the classifying space of a finite group G, the inertia orbifold is the stack quotient G/G, where G acts on itself by conjugation. For this special case, Hinich's result specializes to the assertion that the center of the category of G-representations (with respect to some ground field k) is equivalent to the category consisting of G-graded k-vector spaces, i.e., objects of the form
for some k-vector spaces, together with G-equivariant morphisms, where G acts on itself by conjugation.
In the same vein, (Ben-Zvi Francis) have shown that Drinfeld center of the derived category of quasi-coherent sheaves on a perfect stack X is the derived category of sheaves on the loop stack of X.
Related notions
Centers of monoid objects
The center of a monoid and the Drinfeld center of a monoidal category are both instances of the following more general concept. Given a monoidal category C and a monoid object A in C, the center of A is defined as
For C being the category of sets (with the usual cartesian product), a monoid object is simply a monoid, and Z(A) is the center of the monoid. Similarly, if C is the category of abelian groups, monoid objects are rings, and the above recovers the center of a ring. Finally, if C is the category of categories, with the product as the monoidal operation, monoid objects in C are monoidal categories, and the above recovers the Drinfeld center.
Categorical trace
The categorical trace of a monoidal category (or monoidal ∞-category) is defined as
The concept is being widely applied, for example in (Zhu 2018).
References
- ↑ Majid 1991.
- ↑ (Ben-Zvi Francis)
- Ben-Zvi, David; Francis, John; Nadler, David (2010), "Integral transforms and Drinfeld centers in derived algebraic geometry", Journal of the American Mathematical Society 23 (4): 909–966, doi:10.1090/S0894-0347-10-00669-7
- Hinich, Vladimir (2007), "Drinfeld double for orbifolds", Israel mathematical conference proceedings. Quantum groups. Proceedings of a conference in memory of Joseph Donin, Haifa, Israel, July 5--12, 2004, AMS, pp. 251–265, ISBN 978-0-8218-3713-9
- "Tortile Yang-Baxter operators in tensor categories", Journal of Pure and Applied Algebra 71 (1): 43–51, 1991, doi:10.1016/0022-4049(91)90039-5.
- Lurie, Jacob (2017), Higher Algebra, http://www.math.harvard.edu/~lurie/
- "Representations, duals and quantum doubles of monoidal categories". 1991. 197–206. https://eudml.org/doc/220868.
- Zhu, Xinwen (2018). "Geometric Satake, categorical traces, and arithmetic of Shimura varieties". Current Developments in Mathematics 2016: 145–206. doi:10.4310/CDM.2016.v2016.n1.a4. ISBN 9781571463586. OCLC 1038481072.
External links
 |
Categories: [Category theory]
↧ Download as ZWI file | Last modified: 01/19/2026 20:59:28 | 40 views
☰ Source: https://handwiki.org/wiki/Center_(category_theory) | License: CC BY-SA 3.0
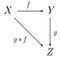

 KSF
KSF