Truncated Tetrapentagonal Tiling

In geometry, the truncated tetrapentagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t_0,1,2{4,5} or tr{4,5}.

Symmetry

Truncated tetrapentagonal tiling with mirror lines.

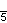
There are four small index subgroup constructed from [5,4] by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.

A radical subgroup is constructed [5*,4], index 10, as [5⁺,4], (5*2) with gyration points removed, becoming orbifold (*22222), and its direct subgroup [5*,4]⁺, index 20, becomes orbifold (22222).

Small index subgroups of [5,4]
Index	1	2		10
Diagram
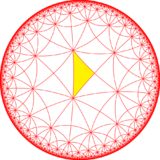
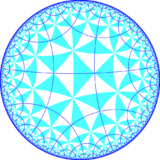
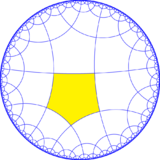
Coxeter (orbifold)	[5,4] = (*542)	[5,4,1+] = = (*552)	[5+,4] = (5*2)	[5*,4] = (*22222)
Direct subgroups
Index	2	4		20
Diagram
Coxeter (orbifold)	[5,4]+ = (542)	[5+,4]+ = = (552)		[5*,4]+ = (22222)

Related polyhedra and tiling

See also

• Uniform tilings in hyperbolic plane
• List of regular polytopes

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• Coxeter, H. S. M. (1999). "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. ISBN 0-486-40919-8. 

External links

• Weisstein, Eric W.. "Hyperbolic tiling". http://mathworld.wolfram.com/HyperbolicTiling.html. 
• Weisstein, Eric W.. "Poincaré hyperbolic disk". http://mathworld.wolfram.com/PoincareHyperbolicDisk.html. 
• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Truncated tetrapentagonal tiling. Read more