List Of Photonics Equations

This article summarizes equations in the theory of photonics, including geometric optics, physical optics, radiometry, diffraction, and interferometry.

Definitions

Geometric optics (luminal rays)

Main page: Physics:Geometrical optics

General fundamental quantities

Quantity (common name/s)	(Common) symbol/s	SI units	Dimension
Object distance	x, s, d, u, x1, s1, d1, u1	m	[L]
Image distance	x', s', d', v, x2, s2, d2, v2	m	[L]
Object height	y, h, y1, h1	m	[L]
Image height	y', h', H, y2, h2, H2	m	[L]
Angle subtended by object	θ, θo, θ1	rad	dimensionless
Angle subtended by image	θ', θi, θ2	rad	dimensionless
Curvature radius of lens/mirror	r, R	m	[L]
Focal length	f	m	[L]

Quantity (common name/s)	(Common) symbol/s	Defining equation	SI units	Dimension
Lens power	P	[math]\displaystyle{ P = 1/f \,\! }[/math]	m−1 = D (dioptre)	[L]−1
Lateral magnification	m	[math]\displaystyle{ m = - x_2/x_1 = y_2/y_1 \,\! }[/math]	dimensionless	dimensionless
Angular magnification	m	[math]\displaystyle{ m = \theta_2/\theta_1 \,\! }[/math]	dimensionless	dimensionless

Physical optics (EM luminal waves)

Main page: Physics:Physical optics

There are different forms of the Poynting vector, the most common are in terms of the E and B or E and H fields.

Quantity (common name/s)	(Common) symbol/s	Defining equation	SI units	Dimension
Poynting vector	S, N	[math]\displaystyle{ \mathbf{N} = \frac{1}{\mu_0}\mathbf{E}\times\mathbf{B} = \mathbf{E}\times\mathbf{H} \,\! }[/math]	W m−2	[M][T]−3
Poynting flux, EM field power flow	ΦS, ΦN	[math]\displaystyle{ \Phi_N = \int_S \mathbf{N} \cdot \mathrm{d}\mathbf{S} \,\! }[/math]	W	[M][L]2[T]−3
RMS Electric field of Light	Erms	[math]\displaystyle{ E_\mathrm{rms} = \sqrt{\langle E^2 \rangle} = E/\sqrt{2}\,\! }[/math]	N C−1 = V m−1	[M][L][T]−3[I]−1
Radiation momentum	p, pEM, pr	[math]\displaystyle{ p_{EM} = U/c\,\! }[/math]	J s m−1	[M][L][T]−1
Radiation pressure	Pr, pr, PEM	[math]\displaystyle{ P_{EM} = I/c = p_{EM}/At \,\! }[/math]	W m−2	[M][T]−3

Radiometry

Main page: Astronomy:Radiometry

Visulization of flux through differential area and solid angle. As always [math]\displaystyle{ \mathbf{\hat{n}} \,\! }[/math] is the unit normal to the incident surface A, [math]\displaystyle{ \mathrm{d} \mathbf{A} = \mathbf{\hat{n}}\mathrm{d}A \,\! }[/math], and [math]\displaystyle{ \mathbf{\hat{e}}_{\angle} \,\! }[/math] is a unit vector in the direction of incident flux on the area element, θ is the angle between them. The factor [math]\displaystyle{ \mathbf{\hat{n}} \cdot \mathbf{\hat{e}}_{\angle} \mathrm{d}A = \mathbf{\hat{e}}_{\angle} \cdot \mathrm{d}\mathbf{A} = \cos \theta \mathrm{d}A \,\! }[/math] arises when the flux is not normal to the surface element, so the area normal to the flux is reduced.

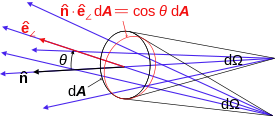
For spectral quantities two definitions are in use to refer to the same quantity, in terms of frequency or wavelength.

Quantity (common name/s)	(Common) symbol/s	Defining equation	SI units	Dimension
Radiant energy	Q, E, Qe, Ee		J	[M][L]2[T]−2
Radiant exposure	He	[math]\displaystyle{ H_e = \mathrm{d} Q/\left ( \mathbf{\hat{e}}_{\angle} \cdot \mathrm{d}\mathbf{A} \right ) \,\! }[/math]	J m−2	[M][T]−3
Radiant energy density	ωe	[math]\displaystyle{ \omega_e = \mathrm{d} Q/\mathrm{d}V \,\! }[/math]	J m−3	[M][L]−3
Radiant flux, radiant power	Φ, Φe	[math]\displaystyle{ Q = \int \Phi \mathrm{d} t }[/math]	W	[M][L]2[T]−3
Radiant intensity	I, Ie	[math]\displaystyle{ \Phi = I \mathrm{d} \Omega \,\! }[/math]	W sr−1	[M][L]2[T]−3
Radiance, intensity	L, Le	[math]\displaystyle{ \Phi = \iint L\left ( \mathbf{\hat{e}}_{\angle} \cdot \mathrm{d}\mathbf{A} \right ) \mathrm{d} \Omega }[/math]	W sr−1 m−2	[M][T]−3
Irradiance	E, I, Ee, Ie	[math]\displaystyle{ \Phi = \int E \left ( \mathbf{\hat{e}}_{\angle} \cdot \mathrm{d}\mathbf{A} \right ) }[/math]	W m−2	[M][T]−3
Radiant exitance, radiant emittance	M, Me	[math]\displaystyle{ \Phi = \int M \left ( \mathbf{\hat{e}}_{\angle} \cdot \mathrm{d}\mathbf{A} \right ) }[/math]	W m−2	[M][T]−3
Radiosity	J, Jν, Je, Jeν	[math]\displaystyle{ J = E + M \,\! }[/math]	W m−2	[M][T]−3
Spectral radiant flux, spectral radiant power	Φλ, Φν, Φeλ, Φeν	[math]\displaystyle{ Q=\iint\Phi_\lambda{\mathrm{d} \lambda \mathrm{d} t} }[/math] [math]\displaystyle{ Q = \iint \Phi_\nu \mathrm{d} \nu \mathrm{d} t }[/math]	W m−1 (Φλ) W Hz−1 = J (Φν)	[M][L]−3[T]−3 (Φλ) [M][L]−2[T]−2 (Φν)
Spectral radiant intensity	Iλ, Iν, Ieλ, Ieν	[math]\displaystyle{ \Phi = \iint I_\lambda \mathrm{d} \lambda \mathrm{d} \Omega }[/math] [math]\displaystyle{ \Phi = \iint I_\nu \mathrm{d} \nu \mathrm{d} \Omega }[/math]	W sr−1 m−1 (Iλ) W sr−1 Hz−1 (Iν)	[M][L]−3[T]−3 (Iλ) [M][L]2[T]−2 (Iν)
Spectral radiance	Lλ, Lν, Leλ, Leν	[math]\displaystyle{ \Phi = \iiint L_\lambda \mathrm{d} \lambda \left ( \mathbf{\hat{e}}_{\angle} \cdot \mathrm{d}\mathbf{A} \right ) \mathrm{d} \Omega }[/math] [math]\displaystyle{ \Phi = \iiint L_\nu \mathrm{d} \nu \left ( \mathbf{\hat{e}}_{\angle} \cdot \mathrm{d}\mathbf{A} \right ) \mathrm{d} \Omega \,\! }[/math]	W sr−1 m−3 (Lλ) W sr−1 m−2 Hz−1 (Lν)	[M][L]−1[T]−3 (Lλ) [M][L]−2[T]−2 (Lν)
Spectral irradiance	Eλ, Eν, Eeλ, Eeν	[math]\displaystyle{ \Phi = \iint E_\lambda \mathrm{d} \lambda \left ( \mathbf{\hat{e}}_{\angle} \cdot \mathrm{d}\mathbf{A} \right ) }[/math] [math]\displaystyle{ \Phi = \iint E_\nu \mathrm{d} \nu \left ( \mathbf{\hat{e}}_{\angle} \cdot \mathrm{d}\mathbf{A} \right ) }[/math]	W m−3 (Eλ) W m−2 Hz−1 (Eν)	[M][L]−1[T]−3 (Eλ) [M][L]−2[T]−2 (Eν)

Equations

Luminal electromagnetic waves

Physical situation	Nomenclature	Equations
Energy density in an EM wave	[math]\displaystyle{ \langle u \rangle \,\! }[/math] = mean energy density	For a dielectric: [math]\displaystyle{ \langle u \rangle = \frac{1}{2} \left ( \epsilon \mathbf{E}^2 + \mu \mathbf{B}^2 \right ) \,\! }[/math]
Kinetic and potential momenta (non-standard terms in use)		Potential momentum: [math]\displaystyle{ \mathbf{p}_\mathrm{p} = q\mathbf{A} \,\! }[/math] Kinetic momentum: [math]\displaystyle{ \mathbf{p}_\mathrm{k} = m\mathbf{v} \,\! }[/math] Cononical momentum: [math]\displaystyle{ \mathbf{p} = m\mathbf{v} + q\mathbf{A} \,\! }[/math]
Irradiance, light intensity	[math]\displaystyle{ \langle \mathbf{S} \rangle \,\! }[/math] = time averaged poynting vector I = irradiance I0 = intensity of source P0 = power of point source Ω = solid angle r = radial position from source	[math]\displaystyle{ I = \langle \mathbf{S} \rangle = E^2_\mathrm{rms}/c\mu_0\,\! }[/math] At a spherical surface: [math]\displaystyle{ I = \frac{P_0}{\Omega \left | r \right |^2}\,\! }[/math]
Doppler effect for light (relativistic)		[math]\displaystyle{ \lambda=\lambda_0\sqrt{\frac{c-v}{c+v}}\,\! }[/math] [math]\displaystyle{ v=|\Delta\lambda|c/\lambda_0\,\! }[/math]
Cherenkov radiation, cone angle	n = refractive index v = speed of particle θ = cone angle	[math]\displaystyle{ \cos \theta = \frac{c}{n v} = \frac{1}{v\sqrt{\epsilon\mu}} \,\! }[/math]
Electric and magnetic amplitudes	E = electric field H = magnetic field strength	For a dielectric [math]\displaystyle{ \left | \mathbf{E} \right | = \sqrt{\frac{\epsilon}{\mu}} \left | \mathbf{H} \right | \,\! }[/math]
EM wave components		Electric [math]\displaystyle{ \mathbf{E} = \mathbf{E}_0 \sin(kx-\omega t)\,\! }[/math] Magnetic [math]\displaystyle{ \mathbf{B} = \mathbf{B}_0 \sin(kx-\omega t)\,\! }[/math]

Geometric optics

Physical situation	Nomenclature	Equations
Critical angle (optics)	n1 = refractive index of initial medium n2 = refractive index of final medium θc = critical angle	[math]\displaystyle{ \sin\theta_c = \frac{n_2}{n_1}\,\! }[/math]
Thin lens equation	f = lens focal length x1 = object length x2 = image length r1 = incident curvature radius r2 = refracted curvature radius	[math]\displaystyle{ \frac{1}{x_1} +\frac{1}{x_2} = \frac{1}{f} \,\! }[/math] Lens focal length from refraction indices [math]\displaystyle{ \frac{1}{f} = \left ( \frac{n_\mathrm{lens}}{{n}_\mathrm{med} }-1 \right )\left ( \frac{1}{r_1} - \frac{1}{r_2} \right )\,\! }[/math]
Image distance in a plane mirror		[math]\displaystyle{ x_2 = -x_1\,\! }[/math]
Spherical mirror	r = curvature radius of mirror	Spherical mirror equation [math]\displaystyle{ \frac{1}{x_1} + \frac{1}{x_2} = \frac{1}{f}= \frac{2}{r}\,\! }[/math] Image distance in a spherical mirror [math]\displaystyle{ \frac{n_1}{x_1} + \frac{n_2}{x_2} = \frac{\left ( n_2 - n_1 \right )}{r}\,\! }[/math]

Subscripts 1 and 2 refer to initial and final optical media respectively.

These ratios are sometimes also used, following simply from other definitions of refractive index, wave phase velocity, and the luminal speed equation:

[math]\displaystyle{ \frac{n_1}{n_2} = \frac{v_2}{v_1} = \frac{\lambda_2}{\lambda_1} = \sqrt{\frac{\epsilon_1 \mu_1}{\epsilon_2 \mu_2}} \,\! }[/math]

where:

Polarization

Physical situation	Nomenclature	Equations
Angle of total polarisation	θB = Reflective polarization angle, Brewster's angle	[math]\displaystyle{ \tan \theta_B = n_2/n_1\,\! }[/math]
intensity from polarized light, Malus's law	I0 = Initial intensity, I = Transmitted intensity, θ = Polarization angle between polarizer transmission axes and electric field vector	[math]\displaystyle{ I = I_0\cos^2\theta\,\! }[/math]

Diffraction and interference

Property or effect	Nomenclature	Equation
Thin film in air	n1 = refractive index of initial medium (before film interference) n2 = refractive index of final medium (after film interference)	Minima: [math]\displaystyle{ N \lambda/n_2\,\! }[/math] Maxima:[math]\displaystyle{ 2L = (N + 1/2)\lambda/n_2\,\! }[/math]
The grating equation	a = width of aperture, slit width α = incident angle to the normal of the grating plane	[math]\displaystyle{ \frac{\delta}{2\pi}\lambda = a \left ( \sin\theta + \sin\alpha \right ) \,\! }[/math]
Rayleigh's criterion		[math]\displaystyle{ \theta_R = 1.22\lambda/\,\!d }[/math]
Bragg's law (solid state diffraction)	d = lattice spacing δ = phase difference between two waves	[math]\displaystyle{ \frac{\delta}{2\pi} \lambda = 2d \sin\theta \,\! }[/math] For constructive interference: [math]\displaystyle{ \delta/2\pi = n \,\! }[/math] For destructive interference: [math]\displaystyle{ \delta/2\pi = n/2 \,\! }[/math] where [math]\displaystyle{ n \in \mathbf{N}\,\! }[/math]
Single slit diffraction intensity	I0 = source intensity Wave phase through apertures [math]\displaystyle{ \phi = \frac{2 \pi a}{\lambda} \sin\theta \,\! }[/math]	[math]\displaystyle{ I = I_0 \left [ \frac{ \sin \left( \phi/2 \right ) }{\left( \phi/2 \right )} \right ]^2 \,\! }[/math]
N-slit diffraction (N ≥ 2)	d = centre-to-centre separation of slits N = number of slits Phase between N waves emerging from each slit [math]\displaystyle{ \delta = \frac{2 \pi d}{\lambda} \sin\theta \,\! }[/math]	[math]\displaystyle{ I = I_0 \left [ \frac{ \sin \left( N \delta/2 \right ) }{\sin \left( \delta/2 \right )} \right ]^2 \,\! }[/math]
N-slit diffraction (all N)		[math]\displaystyle{ I = I_0 \left [ \frac{ \sin \left( \phi/2 \right ) }{\left( \phi/2 \right )} \frac{ \sin \left( N \delta/2 \right ) }{\sin \left( \delta/2 \right )} \right ]^2 \,\! }[/math]
Circular aperture intensity	a = radius of the circular aperture J1 is a Bessel function	[math]\displaystyle{ I = I_0 \left ( \frac{2 J_1(ka \sin \theta)}{ka \sin \theta} \right )^2 }[/math]
Amplitude for a general planar aperture	Cartesian and spherical polar coordinates are used, xy plane contains aperture A, amplitude at position r r' = source point in the aperture Einc, magnitude of incident electric field at aperture	Near-field (Fresnel) [math]\displaystyle{ A\left ( \mathbf{r} \right ) \propto \iint_\mathrm{aperture} E_\mathrm{inc} \left ( \mathbf{r}' \right )~ \frac{e^{ik \left | \mathbf{r} - \mathbf{r}' \right |}}{4 \pi \left | \mathbf{r} - \mathbf{r}' \right |} \mathrm{d}x'\mathrm{d}y' }[/math] Far-field (Fraunhofer) [math]\displaystyle{ A \left ( \mathbf{r} \right ) \propto \frac{e^{ik r}}{4 \pi r} \iint_\mathrm{aperture} E_\mathrm{inc}\left ( \mathbf{r}' \right ) e^{-ik \left [ \sin \theta \left ( \cos \phi x' + \sin \phi y' \right ) \right ] } \mathrm{d}x'\mathrm{d}y' }[/math]
Huygen-Fresnel-Kirchhoff principle	r0 = position from source to aperture, incident on it r = position from aperture diffracted from it to a point α0 = incident angle with respect to the normal, from source to aperture α = diffracted angle, from aperture to a point S = imaginary surface bounded by aperture [math]\displaystyle{ \mathbf{\hat{n}}\,\! }[/math] = unit normal vector to the aperture [math]\displaystyle{ \mathbf{r}_0 \cdot \mathbf{\hat{n}} = \left | \mathbf{r}_0 \right | \cos \alpha_0 \,\! }[/math] [math]\displaystyle{ \mathbf{r} \cdot \mathbf{\hat{n}} = \left | \mathbf{r} \right | \cos \alpha \,\! }[/math] [math]\displaystyle{ \left | \mathbf{r} \right |\left | \mathbf{r}_0 \right | \ll \lambda \,\! }[/math]	[math]\displaystyle{ A \mathbf ( \mathbf{r} ) = \frac{-i}{2\lambda} \iint_\mathrm{aperture} \frac{e^{i \mathbf{k} \cdot \left ( \mathbf{r} + \mathbf{r}_0 \right ) }}{ \left | \mathbf{r} \right |\left | \mathbf{r}_0 \right |} \left [ \cos \alpha_0 - \cos \alpha \right ] \mathrm{d}S \,\! }[/math]
Kirchhoff's diffraction formula		[math]\displaystyle{ A \left ( \mathbf{r} \right ) = - \frac{1}{4 \pi} \iint_\mathrm{aperture} \frac{e^{i \mathbf{k} \cdot \mathbf{r}_0}}{\left | \mathbf{r}_0 \right |} \left[ i \left | \mathbf{k} \right | U_0 \left ( \mathbf{r}_0 \right ) \cos{\alpha} + \frac {\partial A_0 \left ( \mathbf{r}_0 \right )}{\partial n} \right ] \mathrm{d}S }[/math]

Astrophysics definitions

In astrophysics, L is used for luminosity (energy per unit time, equivalent to power) and F is used for energy flux (energy per unit time per unit area, equivalent to intensity in terms of area, not solid angle). They are not new quantities, simply different names.

Quantity (common name/s)	(Common) symbol/s	Defining equation	SI units	Dimension
Comoving transverse distance	DM		pc (parsecs)	[L]
Luminosity distance	DL	[math]\displaystyle{ D_L = \sqrt{\frac{L}{4\pi F}} \, }[/math]	pc (parsecs)	[L]
Apparent magnitude in band j (UV, visible and IR parts of EM spectrum) (Bolometric)	m	[math]\displaystyle{ m_j= -\frac{5}{2} \log_{10} \left | \frac {F_j}{F_j^0} \right | \, }[/math]	dimensionless	dimensionless
Absolute magnitude (Bolometric)	M	[math]\displaystyle{ M = m - 5 \left [ \left ( \log_{10}{D_L} \right ) - 1 \right ]\!\, }[/math]	dimensionless	dimensionless
Distance modulus	μ	[math]\displaystyle{ \mu = m - M \!\, }[/math]	dimensionless	dimensionless
Colour indices	(No standard symbols)	[math]\displaystyle{ U-B = M_U - M_B\!\, }[/math] [math]\displaystyle{ B-V = M_B - M_V\!\, }[/math]	dimensionless	dimensionless
Bolometric correction	Cbol (No standard symbol)	[math]\displaystyle{ \begin{align} C_\mathrm{bol} & = m_\mathrm{bol} - V \\ & = M_\mathrm{bol} - M_V \end{align} \!\, }[/math]	dimensionless	dimensionless

See also

• Defining equation
• Defining equation (physical chemistry)
• List of electromagnetism equations
• List of equations in classical mechanics
• List of equations in gravitation
• List of equations in nuclear and particle physics
• List of equations in quantum mechanics
• List of equations in wave theory
• List of relativistic equations

Sources

• P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 0-7195-3382-1. 
• G. Woan (2010). The Cambridge Handbook of Physics Formulas. Cambridge University Press. ISBN 978-0-521-57507-2. https://archive.org/details/cambridgehandboo0000woan. 
• A. Halpern (1988). 3000 Solved Problems in Physics, Schaum Series. Mc Graw Hill. ISBN 978-0-07-025734-4. 
• R.G. Lerner; G.L. Trigg (2005). Encyclopaedia of Physics (2nd ed.). VHC Publishers, Hans Warlimont, Springer. pp. 12–13. ISBN 978-0-07-025734-4. 
• C.B. Parker (1994). McGraw Hill Encyclopaedia of Physics (2nd ed.). McGraw Hill. ISBN 0-07-051400-3. https://archive.org/details/mcgrawhillencycl1993park. 
• P.A. Tipler; G. Mosca (2008). Physics for Scientists and Engineers: With Modern Physics (6th ed.). W.H. Freeman and Co. ISBN 978-1-4292-0265-7. 
• L.N. Hand; J.D. Finch (2008). Analytical Mechanics. Cambridge University Press. ISBN 978-0-521-57572-0. 
• T.B. Arkill; C.J. Millar (1974). Mechanics, Vibrations and Waves. John Murray. ISBN 0-7195-2882-8. 
• H.J. Pain (1983). The Physics of Vibrations and Waves (3rd ed.). John Wiley & Sons. ISBN 0-471-90182-2. 
• J.R. Forshaw; A.G. Smith (2009). Dynamics and Relativity. Wiley. ISBN 978-0-470-01460-8. 
• G.A.G. Bennet (1974). Electricity and Modern Physics (2nd ed.). Edward Arnold (UK). ISBN 0-7131-2459-8. 
• I.S. Grant; W.R. Phillips; Manchester Physics (2008). Electromagnetism (2nd Edition). John Wiley & Sons. ISBN 978-0-471-92712-9. 
• D.J. Griffiths (2007). Introduction to Electrodynamics (3rd ed.). Pearson Education, Dorling Kindersley. ISBN 81-7758-293-3. 

Further reading

• L.H. Greenberg (1978). Physics with Modern Applications. Holt-Saunders International W.B. Saunders and Co. ISBN 0-7216-4247-0. https://archive.org/details/physicswithmoder0000gree. 
• J.B. Marion; W.F. Hornyak (1984). Principles of Physics. Holt-Saunders International Saunders College. ISBN 4-8337-0195-2. 
• A. Beiser (1987). Concepts of Modern Physics (4th ed.). McGraw-Hill (International). ISBN 0-07-100144-1. 
• H.D. Young; R.A. Freedman (2008). University Physics – With Modern Physics (12th ed.). Addison-Wesley (Pearson International). ISBN 0-321-50130-6. 

0.00 (0 votes)