Range
 From Conservapedia
From Conservapedia In mathematics, the range (or image) of a function are the values it hits. It is not to be confused with the codomain of a function, which is a designated set to which all the values of the function belong.
A function is onto (or surjective) if every value in its codomain is hit by the function, or, equivalently, if its range is equal to its codomain. More formally, a function 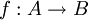 is onto if for every
is onto if for every  there exists
there exists  such that
such that
 .
.
Examples[edit]
Let  be the function defined by the equation
be the function defined by the equation 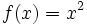 . By definition, the codomain
of
. By definition, the codomain
of  is
is  . However, the range of
. However, the range of 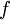 consists of all nonnegative real numbers. Indeed, let
consists of all nonnegative real numbers. Indeed, let 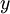 be a nonnegative real number. Then
be a nonnegative real number. Then  , and so
, and so 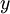 is one of the values hit by
is one of the values hit by 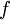 .
.
Let  be the function defined by the equation
be the function defined by the equation 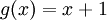 . Then, for every real number
. Then, for every real number
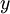 , we can see that
, we can see that 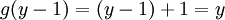 , so every real number is hit by
, so every real number is hit by 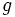 . This means that the codomain and range of
. This means that the codomain and range of 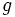 are equal, namely
are equal, namely 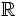 . Therefore,
. Therefore, 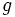 is onto.
is onto.
Non-mathematical uses[edit]
- A range can also refer to a type of oven.
- Shooting range
- Range - see distance and rangefinder in target and sniper shooting
Categories: [Mathematics] [Firearms Glossary] [Firearms]
↧ Download as ZWI file | Last modified: 02/15/2023 23:16:14 | 115 views
☰ Source: https://www.conservapedia.com/Range | License: CC BY-SA 3.0
 ZWI signed:
ZWI signed: KSF
KSF