Radioactivity
 From Conservapedia
From Conservapedia Radioactivity is the emission of high energy particles through the natural phenomenon of the decay of unstable isotopes of chemical elements into more stable forms, which are called daughter products. This type of emission is generally called nuclear radiation.
The most common types of nuclear radiation are alpha, beta, and gamma radiation, and the processes for each are respectively alpha decay, beta decay, and gamma decay.[1] Alpha particles are helium nuclei (two protons and two neutrons); beta particles are high-energy electrons; gamma rays are high-energy photons. Alpha particles can normally be stopped by a sheet of paper or healthy human skin. Beta particles and gamma rays can penetrate one's body to cause great harm. Gamma radiation is also a form of electro-magnetic radiation, like X-rays or visible light. (Contemporary jargon refers to alpha and beta particles and gamma rays, though quantum mechanics makes the two actually the same.)
All forms of radioactivity follow the fundamental rules of mass and energy conservation, taking into account their interrelationship due to the formula E=mc². In fact, radioactive decay illustrates this formula clearly, while chemical transformations involve a mass change so small as to be imperceptible.
Contents
Alpha Decay[edit]
- Main article: Alpha decay
As stated above, an alpha particle is the nucleus of a Helium atom, i.e., two protons and two neutrons. This arrangement means the alpha particle has a charge of +2, and an atomic mass of 4, the symbol for which is 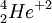 .
.
For example, the most common isotope of Uranium is Uranium-238. The mass number,[2] 238, is the sum of the number of protons and the number of neutrons. Since all Uranium atoms have 92 protons, there are 146 neutrons. The initial step in Uranium-238 decaying (eventually) into Lead-206 is an alpha decay:
 →
→ 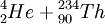
Note that the proton count (92) is conserved, as is are the mass numbers (238). So the neutron count (146) is also balanced. No particles are created or destroyed; they are simply pulled apart.
This decay releases about 4.3 MeV of kinetic energy, in the form of the motion of the alpha particle. In chemical terms we would say that this decay is an exothermic reaction. The energy comes from the potential nuclear energy of the Uranium atom—the Uranium atom has a higher potential energy (by 4.3 Mev) than the sum of the potential energies of the Thorium and Helium atoms. A careful accounting of the atomic masses (remember, atomic mass is only approximately equal to mass number) will show that mass was lost, in accordance with E=mc².
Beta Decay[edit]
- Main article: Beta decay
As stated above, a beta particle is an electron. This arrangement means the beta particle has a charge of -1, and an atomic mass of 0, the symbol for which is  .
.
Strontium-90 undergoes beta decay to form Yttrium-90 in the following decay reaction:
 →
→ 
As with the alpha decay, notice that the particle count is again conserved. The energy released by this decay is 0.55 MeV.
An interesting note about Strontium-90 is that is a synthetic isotope (meaning, it is not found naturally occurring, but must be manufactured) that is a by-product of nuclear weapons explosions. In the 1950s and 1960s, it was common to test nuclear weapons by exploding them in the very high upper atmosphere. Unfortunately, this resulted in a large amount of Strontium-90 particles that eventually settled back to earth, contaminating grass lands. The grasses were eaten by cattle, and the cattle were eaten (and their milk consumed) by humans.
Since Strontium is chemically very similar to Calcium (it is in the same column in the Periodic Table), any entrance of Strontium in the body will tend to replace the Calcium in our bones. In the case of Strontium-90, this meant that radioactive Strontium was now chemically bonded to people's bones, and the 1970s saw a rise in bone cancer as a result. Fortunately, this type of testing was halted, and the half-life of Strontium-90 is a relatively short 28 years, meaning, at this point most of the synthetic, radioactive Strontium-90 produced by weapons testing has decayed out of the environment.
Energy of Radioactive Decay[edit]
The energies associated with radioactive decay, at least on the single atom level, are very, very small. The energies are so small, in fact, we use a special unit called the Electron Volt (eV) rather than the traditional units of Joules or Btu or Foot-pounds.
Just for a point of comparison, it takes about a minute to boil a cup of water in a 1000 Watt microwave. One Watt is equivalent to one Joule per second, so it takes 60,000 Joules of energy to boil a cup of water. But a single Joule of energy is the same as 6.24x1018 eV!
So even when a nuclear decay has an associated energy in the thousands (keV) or millions (MeV) of electron volts, the decay of one atom is still billions of factors away from having enough energy to boil a cup of water. But, when measured in the more usual way, of Joules per kilogram of reactant, the energy release is enormous. The energy released by the decay of 1 gram of Polonium-210 is 2.5x1013 Joules. (It isn't released all at once; the half-life is 138 days.)
Exponential decay and half-life[edit]
Although the exact mechanisms of alpha, beta, and gamma decay are quite different, all three are dictated by the rules of quantum mechanics. These rules dictate a fixed probability, per second, that a nucleus will decay. So a nucleus has some probability, say P, surviving one second without decaying. For Polonium-210, P=.99999994, for example. For Uranium-238, P=.999999999999999995.
After 2 seconds, the fraction of material left is P2. After 10 seconds, it is P10, and so on. So the fraction remaining is an exponential function of time. This is the reason for the characteristic exponential decay of radioactive substances. The type of decay doesn't matter; the decay is always exponential. The usual way this is described is the half-life, which is the time for one half of the sample to disintegrate. The half-life can be seen to be log(1/2) / log(P). Half-lives can vary from quantities like 10-21 seconds for Beryllium-13, to 1018 years (far more than the age of the universe) for Tungsten-182.
Since the rate at which radiation is emitted is proportional to the amount of the substance present, and the amount of substance remaining undergoes exponential decay, the rate of particle emission (e.g. Geiger counter clicks per second) also decays exponentially.
Specifically, the formula for the fraction of substance remaining after time t is:
where H is the half-life.
While the mechanisms for decay, and hence the half-lives of various isotopes, are well understood on theoretical grounds, the calculations are so complex that half-lives are measured experimentally. The measured half-lives of the various isotopes of elements are known to be fixed quite accurately. Careful astronomical observations show that half-lives have not changed significantly in billions of years—spectral lines from distant galaxies would have shifted perceptibly if the constants involved had changed. In some cases radioactive decay itself can be observed and measured in distant galaxies when a supernova explodes and ejects radioactive nuclei.
The fundamental physical principles underlying radioactive decay are quite precise and based on quantum mechanics, but the overall decay rate of a given sample is subject to slight dependence on external conditions. These conditions involve the electric field in the vicinity of the nucleus, and are the result of the influence of the atom's electron cloud. The electron cloud is relatively very far away (a factor of many millions) from the nucleus, so the effects on the rate of radioactivity are tiny. The largest known effect that can be achieved without a particle accelerator or similar apparatus is about 1.5%, for the beta decay of Beryllium-7. See systematics of beta decay for details.
Antiquated notions[edit]
In the early decades of the 20th century, when it was a newly discovered phenomenon, there was much confusion about it, leading to some strange hypotheses. No less an intellectual than H. G. Wells wrote strange things about it. In his 1909 novel Tono-Bungay, the narrator muses:
- To my mind radio-activity is a real disease of matter. Moreover, it is a contagious disease. It spreads. You bring those debased and crumbling atoms near others and those too presently catch the trick of swinging themselves out of coherent existence. It is in matter exactly what the decay of our old culture is in society, a loss of traditions and distinctions and assured reactions. ...I am haunted by a grotesque fancy of the ultimate eating away and dry-rotting and dispersal of all our world. So that while man still struggles and dreams his very substance will change and crumble from beneath him. I mention this here as a queer persistent fancy. Suppose, indeed, that is to be the end of our planet; no splendid climax and finale, no towering accumulation of achievements, but just—atomic decay![3]
This is not to say that radioactivity isn't dangerous, or that radioactive contamination isn't a tricky problem.
See also[edit]
Notes and references[edit]
- ↑ http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/radact.html
- ↑ The mass number is the (integer) number of nucleons. It is very close to the atomic mass of the isotope measured in amu, because the masses of protons and neutrons are very close, and the deviations (due to E=mc²) are small. So the terms are often used nearly interchangeably.
- ↑ Wells, H. G. (1909) Tono-Bungay, online Project Gutenberg text; search for text string "real disease"
Categories: [Radioactivity]
↧ Download as ZWI file | Last modified: 02/04/2023 06:14:42 | 103 views
☰ Source: https://www.conservapedia.com/Radioactivity | License: CC BY-SA 3.0
 ZWI signed:
ZWI signed: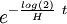
 KSF
KSF