Markov Braid Theorem
 From Encyclopediaofmath
From Encyclopediaofmath If two closed braids represent the same ambient isotopy class of oriented links (cf. also Braid theory), then one can transform one braid to another by a sequence of Markov moves:
i) $a \leftrightarrow b a b ^ { - 1 }$ (conjugation).
ii) $a \leftrightarrow a b ^ { \pm 1 }_ { n }$, where $a$ is an element of the $n$th braid group
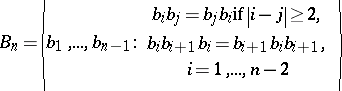 |
and $b _ { n }$ is the $n$th generator of the $( n + 1 )$th braid group.
Markov's braid theorem is an important ingredient in the construction of the Jones polynomial and its generalizations (e.g. the Jones–Conway polynomial).
References[edit]
| [a1] | J.S. Birman, "Braids, links and mapping class groups", Ann. of Math. Stud., 82 , Princeton Univ. Press (1974) |
| [a2] | A.A. Markov, "Über die freie Äquivalenz der geschlossenen Zöpfe", Recueil Math. Moscou, 1 (1935) pp. 73–78 Zbl 0014.04202 |
| [a3] | N.M. Weinberg, "On free equivalence of free braids", C.R. (Dokl.) Acad. Sci. USSR, 23 (1939) pp. 215–216 (In Russian) |
↧ Download as ZWI file | Last modified: 11/06/2025 21:31:41 | 1 views
☰ Source: https://encyclopediaofmath.org/wiki/Markov_braid_theorem | License: CC BY-SA 3.0
✘
ZWI is not signed. [what is this?]
 KSF
KSF