Inner Product

In linear algebra, an inner product 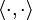in a vector space 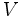is a function from to 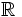satisfying the following axioms for all vectors 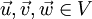:^[1]

• , with 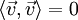if and only if ,
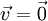• (the inner product is commutative),
• , and
• for all , .

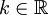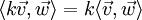One consequence of the inner product axioms is that the inner product is multilinear in both variables; that is:

The dot product in the Euclidean vector space 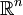is the best-known example of an inner product.

An inner product space is a vector space together with an inner product.

References[edit]

1. ↑ Anton, Howard and Chris Rorres. Elementary Linear Algebra: Applications Version. 9th ed. N.p.:John Wiley & Sons, Inc., 2005. p. 296