Uniform Limit Theorem

Counterexample to a strengthening of the uniform limit theorem, in which pointwise convergence, rather than uniform convergence, is assumed. The continuous green functions [math]\displaystyle{ \scriptstyle \scriptstyle\sin^n(x) }[/math] converge to the non-continuous red function. This can happen only if convergence is not uniform.

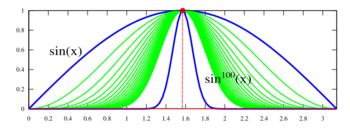
In mathematics, the uniform limit theorem states that the uniform limit of any sequence of continuous functions is continuous.

Statement

More precisely, let X be a topological space, let Y be a metric space, and let ƒ_n : X → Y be a sequence of functions converging uniformly to a function ƒ : X → Y. According to the uniform limit theorem, if each of the functions ƒ_n is continuous, then the limit ƒ must be continuous as well.

This theorem does not hold if uniform convergence is replaced by pointwise convergence. For example, let ƒ_n : [0, 1] → R be the sequence of functions ƒ_n(x) = xⁿ. Then each function ƒ_n is continuous, but the sequence converges pointwise to the discontinuous function ƒ that is zero on [0, 1) but has ƒ(1) = 1. Another example is shown in the adjacent image.

In terms of function spaces, the uniform limit theorem says that the space C(X, Y) of all continuous functions from a topological space X to a metric space Y is a closed subset of Y^X under the uniform metric. In the case where Y is complete, it follows that C(X, Y) is itself a complete metric space. In particular, if Y is a Banach space, then C(X, Y) is itself a Banach space under the uniform norm.

The uniform limit theorem also holds if continuity is replaced by uniform continuity. That is, if X and Y are metric spaces and ƒ_n : X → Y is a sequence of uniformly continuous functions converging uniformly to a function ƒ, then ƒ must be uniformly continuous.

Proof

In order to prove the continuity of f, we have to show that for every ε > 0, there exists a neighbourhood U of any point x of X such that:

[math]\displaystyle{ d_Y(f(x),f(y)) \lt \varepsilon, \qquad\forall y \in U }[/math]

Consider an arbitrary ε > 0. Since the sequence of functions (f_n) converges uniformly to f by hypothesis, there exists a natural number N such that:

[math]\displaystyle{ d_Y(f_N(t),f(t)) \lt \frac{\varepsilon}{3}, \qquad\forall t \in X }[/math]

Moreover, since f_N is continuous on X by hypothesis, for every x there exists a neighbourhood U such that:

[math]\displaystyle{ d_Y(f_N(x),f_N(y)) \lt \frac{\varepsilon}{3}, \qquad\forall y \in U }[/math]

In the final step, we apply the triangle inequality in the following way:

[math]\displaystyle{ \begin{align} d_Y(f(x),f(y)) & \leq d_Y(f(x),f_N(x)) + d_Y(f_N(x),f_N(y)) + d_Y(f_N(y),f(y)) \\ & \lt \frac{\varepsilon}{3} + \frac{\varepsilon}{3} + \frac{\varepsilon}{3} = \varepsilon, \qquad \forall y \in U \end{align} }[/math]

Hence, we have shown that the first inequality in the proof holds, so by definition f is continuous everywhere on X.

Uniform limit theorem in complex analysis

There are also variants of the uniform limit theorem that are used in complex analysis, albeit with modified assumptions.

Theorem.^[1] Let [math]\displaystyle{ \Omega }[/math] be an open and connected subset of the complex numbers. Suppose that [math]\displaystyle{ (f_n)_{n=1}^{\infty} }[/math] is a sequence of holomorphic functions [math]\displaystyle{ f_n:\Omega\to \mathbb{C} }[/math] that converges uniformly to a function [math]\displaystyle{ f:\Omega \to \mathbb{C} }[/math] on every compact subset of [math]\displaystyle{ \Omega }[/math]. Then [math]\displaystyle{ f }[/math] is holomorphic in [math]\displaystyle{ \Omega }[/math], and moreover, the sequence of derivatives [math]\displaystyle{ (f'_n)_{n=1}^{\infty} }[/math] converges uniformly to [math]\displaystyle{ f' }[/math] on every compact subset of [math]\displaystyle{ \Omega }[/math].

Theorem.^[2] Let [math]\displaystyle{ \Omega }[/math] be an open and connected subset of the complex numbers. Suppose that [math]\displaystyle{ (f_n)_{n=1}^{\infty} }[/math] is a sequence of univalent^[3] functions [math]\displaystyle{ f_n:\Omega\to \mathbb{C} }[/math] that converges uniformly to a function [math]\displaystyle{ f:\Omega \to \mathbb{C} }[/math]. Then [math]\displaystyle{ f }[/math] is holomorphic, and moreover, [math]\displaystyle{ f }[/math] is either univalent or constant in [math]\displaystyle{ \Omega }[/math].

Notes

References

• James Munkres (1999). Topology (2nd ed.). Prentice Hall. ISBN 0-13-181629-2. 

• E. M. Stein, R. Shakarachi (2003). Complex Analysis (Princeton Lectures in Analysis, No. 2), Princeton University Press, pp.53-54.

• E. C. Titchmarsh (1939). The Theory of Functions, 2002 Reprint, Oxford Science Publications.

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Uniform limit theorem. Read more