Hyperbolic Trigonometric Functions
 From Conservapedia
From Conservapedia The hyperbolic trigonometric functions, also referred to as simply "hyperbolic functions," are analogous to the standard trigonometric functions using a hyperbola as the defining conic section rather than a circle.[1] This has the effect of removing any i's that appear in the complex definition of the standard trigonometric functions. As such, they tend to differentiate in an analogous way to standard trigonometric functions, up to perhaps a negative sign. They are defined as:
- Hyperbolic sine:

- Hyperbolic cosine:

- Hyperbolic tangent:

- Hyperbolic cosecant:

- Hyperbolic secant:

- Hyperbolic cotangent:

Contents
- 1 Graphs
- 2 Identities
- 3 References
- 4 See also
Graphs[edit]

|

|
| sinh and cosh | tanh and coth |
Identities[edit]
The hyperbolic trigonometric functions have many identities that are similar to those of trigonometric functions. These can be remembered by replacing instances of  with
with  . For example, the trigonometric identity,
. For example, the trigonometric identity,
has the corresponding hyperbolic identity,
Other identities include:
Also, note that:
References[edit]
- ↑ Hyperbolic functions from mathworld.wolfram.com
See also[edit]
- Trigonometric function
Categories: [Trigonometry]
↧ Download as ZWI file | Last modified: 03/26/2023 22:53:13 | 10 views
☰ Source: https://www.conservapedia.com/Hyperbolic_trigonometric_functions | License: CC BY-SA 3.0
 ZWI signed:
ZWI signed:


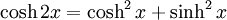


 KSF
KSF