Rational Tangles

A family of $2$-tangles (cf. Tangle) classified by J.H. Conway. The $2$-tangle of Fig. a1 is called a rational tangle with Conway notation $T ( a _ { 1 } , \dots , a _ { n } )$. It is a rational $p / q$-tangle if

\begin{equation*} \frac { p } { q } = a _ { n } + \frac { 1 } { a _ { n - 1} + \ldots + \frac { 1 } { a_ { 1 } } }. \end{equation*}

The fraction $p / q$ is called the slope of the tangle and can be identified with the slope of the meridian disc of the solid torus that is the branched double covering of the rational tangle.

Figure: r130030a

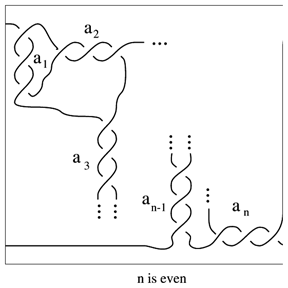
Figure: r130030b

Conway proved that two rational tangles are ambient isotopic (with boundary fixed) if and only if their slopes are equal. A rational $n$-tangle (also called an $n$-bridge $n$-tangle) is an $n$-tangle that can be obtained from the identity tangle by a finite number of additions of a single crossing.

References[edit]

• [a1] J.H. Conway, "An enumeration of knots and links" J. Leech (ed.), Computational Problems in Abstract Algebra, Pergamon Press (1969) pp. 329–358 Zbl 0202.54703
• [a2] A. Kawauchi, "A survey of knot theory", Birkhäuser (1996) Zbl 0861.57001