Special Relativity
 From Handwiki
From Handwiki In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between space and time. In Albert Einstein's 1905 treatment, the theory is presented as being based on just two postulates:[p 1][1][2]
- The laws of physics are invariant (identical) in all inertial frames of reference (that is, frames of reference with no acceleration).
- The speed of light in vacuum is the same for all observers, regardless of the motion of light source or observer.
The first postulate was first formulated by Galileo Galilei (see Galilean invariance).
Origins and significance
Special relativity was described by Albert Einstein in a paper published on 26 September 1905 titled "On the Electrodynamics of Moving Bodies".[p 1] Maxwell's equations of electromagnetism appeared to be incompatible with Newtonian mechanics, and the Michelson–Morley null result failed to detect the Earth's motion against the hypothesized luminiferous aether. These led to the development of the Lorentz transformations, which adjust distances and times for moving objects. Special relativity corrects the hitherto laws of mechanics to handle situations involving all motions and especially those at a speed close to that of light (known as relativistic velocities). Today, special relativity is proven to be the most accurate model of motion at any speed when gravitational and quantum effects are negligible.[3][4] Even so, the Newtonian model is still valid as a simple and accurate approximation at low velocities (relative to the speed of light), for example, everyday motions on Earth.
Special relativity has a wide range of consequences that have been experimentally verified.[5] They include the relativity of simultaneity, length contraction, time dilation, the relativistic velocity addition formula, the relativistic Doppler effect, relativistic mass, a universal speed limit, mass–energy equivalence, the speed of causality and the Thomas precession.[1][2] It has, for example, replaced the conventional notion of an absolute universal time with the notion of a time that is dependent on reference frame and spatial position. Rather than an invariant time interval between two events, there is an invariant spacetime interval. Combined with other laws of physics, the two postulates of special relativity predict the equivalence of mass and energy, as expressed in the mass–energy equivalence formula [math]\displaystyle{ E = mc^2 }[/math], where [math]\displaystyle{ c }[/math] is the speed of light in a vacuum.[6][7] It also explains how the phenomena of electricity and magnetism are related.[1][2]
A defining feature of special relativity is the replacement of the Galilean transformations of Newtonian mechanics with the Lorentz transformations. Time and space cannot be defined separately from each other (as was previously thought to be the case). Rather, space and time are interwoven into a single continuum known as "spacetime". Events that occur at the same time for one observer can occur at different times for another.
Until several years later when Einstein developed general relativity, which introduced a curved spacetime to incorporate gravity, the phrase "special relativity" was not used. A translation sometimes used is "restricted relativity"; "special" really means "special case".[p 2][p 3][p 4][note 1] Some of the work of Albert Einstein in special relativity is built on the earlier work by Hendrik Lorentz and Henri Poincaré. The theory became essentially complete in 1907, with Hermann Minkowski's papers on spacetime.[4]
The theory is "special" in that it only applies in the special case where the spacetime is "flat", that is, where the curvature of spacetime (a consequence of the energy–momentum tensor and representing gravity) is negligible.[8][note 2] To correctly accommodate gravity, Einstein formulated general relativity in 1915. Special relativity, contrary to some historical descriptions, does accommodate accelerations as well as accelerating frames of reference.[9][10]
Just as Galilean relativity is now accepted to be an approximation of special relativity that is valid for low speeds, special relativity is considered an approximation of general relativity that is valid for weak gravitational fields, that is, at a sufficiently small scale (e.g., when tidal forces are negligible) and in conditions of free fall. But general relativity incorporates non-Euclidean geometry to represent gravitational effects as the geometric curvature of spacetime. Special relativity is restricted to the flat spacetime known as Minkowski space. As long as the universe can be modeled as a pseudo-Riemannian manifold, a Lorentz-invariant frame that abides by special relativity can be defined for a sufficiently small neighborhood of each point in this curved spacetime.
Galileo Galilei had already postulated that there is no absolute and well-defined state of rest (no privileged reference frames), a principle now called Galileo's principle of relativity. Einstein extended this principle so that it accounted for the constant speed of light,[11] a phenomenon that had been observed in the Michelson–Morley experiment. He also postulated that it holds for all the laws of physics, including both the laws of mechanics and of electrodynamics.[12]
Traditional "two postulates" approach to special relativity
Albert Einstein: Autobiographical Notes[p 5]
Einstein discerned two fundamental propositions that seemed to be the most assured, regardless of the exact validity of the (then) known laws of either mechanics or electrodynamics. These propositions were the constancy of the speed of light in vacuum and the independence of physical laws (especially the constancy of the speed of light) from the choice of inertial system. In his initial presentation of special relativity in 1905 he expressed these postulates as:[p 1]
- The principle of relativity – the laws by which the states of physical systems undergo change are not affected, whether these changes of state be referred to the one or the other of two systems in uniform translatory motion relative to each other.[p 1]
- The principle of invariant light speed – "... light is always propagated in empty space with a definite velocity [speed] c which is independent of the state of motion of the emitting body" (from the preface).[p 1] That is, light in vacuum propagates with the speed c (a fixed constant, independent of direction) in at least one system of inertial coordinates (the "stationary system"), regardless of the state of motion of the light source.
The constancy of the speed of light was motivated by Maxwell's theory of electromagnetism[citation needed] and the lack of evidence for the luminiferous ether. There is conflicting evidence on the extent to which Einstein was influenced by the null result of the Michelson–Morley experiment.[13][14] In any case, the null result of the Michelson–Morley experiment helped the notion of the constancy of the speed of light gain widespread and rapid acceptance.
The derivation of special relativity depends not only on these two explicit postulates, but also on several tacit assumptions (made in almost all theories of physics), including the isotropy and homogeneity of space and the independence of measuring rods and clocks from their past history.[p 6]
Following Einstein's original presentation of special relativity in 1905, many different sets of postulates have been proposed in various alternative derivations.[15] But the most common set of postulates remains those employed by Einstein in his original paper. A more mathematical statement of the principle of relativity made later by Einstein, which introduces the concept of simplicity not mentioned above is:
Special principle of relativity: If a system of coordinates K is chosen so that, in relation to it, physical laws hold good in their simplest form, the same laws hold good in relation to any other system of coordinates K′ moving in uniform translation relatively to K.[16]
Henri Poincaré provided the mathematical framework for relativity theory by proving that Lorentz transformations are a subset of his Poincaré group of symmetry transformations. Einstein later derived these transformations from his axioms.
Many of Einstein's papers present derivations of the Lorentz transformation based upon these two principles.[p 7]
Principle of relativity
Reference frames and relative motion

Reference frames play a crucial role in relativity theory. The term reference frame as used here is an observational perspective in space that is not undergoing any change in motion (acceleration), from which a position can be measured along 3 spatial axes (so, at rest or constant velocity). In addition, a reference frame has the ability to determine measurements of the time of events using a "clock" (any reference device with uniform periodicity).
An event is an occurrence that can be assigned a single unique moment and location in space relative to a reference frame: it is a "point" in spacetime. Since the speed of light is constant in relativity irrespective of the reference frame, pulses of light can be used to unambiguously measure distances and refer back to the times that events occurred to the clock, even though light takes time to reach the clock after the event has transpired.
For example, the explosion of a firecracker may be considered to be an "event". We can completely specify an event by its four spacetime coordinates: The time of occurrence and its 3-dimensional spatial location define a reference point. Let's call this reference frame S.
In relativity theory, we often want to calculate the coordinates of an event from differing reference frames. The equations that relate measurements made in different frames are called transformation equations.
Standard configuration
To gain insight into how the spacetime coordinates measured by observers in different reference frames compare with each other, it is useful to work with a simplified setup with frames in a standard configuration.[17]:107 With care, this allows simplification of the math with no loss of generality in the conclusions that are reached. In Fig. 2-1, two Galilean reference frames (i.e., conventional 3-space frames) are displayed in relative motion. Frame S belongs to a first observer O, and frame S′ (pronounced "S prime" or "S dash") belongs to a second observer O′.
- The x, y, z axes of frame S are oriented parallel to the respective primed axes of frame S′.
- Frame S′ moves, for simplicity, in a single direction: the x-direction of frame S with a constant velocity v as measured in frame S.
- The origins of frames S and S′ are coincident when time t = 0 for frame S and t′ = 0 for frame S′.
Since there is no absolute reference frame in relativity theory, a concept of "moving" does not strictly exist, as everything may be moving with respect to some other reference frame. Instead, any two frames that move at the same speed in the same direction are said to be comoving. Therefore, S and S′ are not comoving.
Lack of an absolute reference frame
The principle of relativity, which states that physical laws have the same form in each inertial reference frame, dates back to Galileo, and was incorporated into Newtonian physics. But in the late 19th century the existence of electromagnetic waves led some physicists to suggest that the universe was filled with a substance they called "aether", which, they postulated, would act as the medium through which these waves, or vibrations, propagated (in many respects similar to the way sound propagates through air). The aether was thought to be an absolute reference frame against which all speeds could be measured, and could be considered fixed and motionless relative to Earth or some other fixed reference point. The aether was supposed to be sufficiently elastic to support electromagnetic waves, while those waves could interact with matter, yet offering no resistance to bodies passing through it (its one property was that it allowed electromagnetic waves to propagate). The results of various experiments, including the Michelson–Morley experiment in 1887 (subsequently verified with more accurate and innovative experiments), led to the theory of special relativity, by showing that the aether did not exist.[18] Einstein's solution was to discard the notion of an aether and the absolute state of rest. In relativity, any reference frame moving with uniform motion will observe the same laws of physics. In particular, the speed of light in vacuum is always measured to be c, even when measured by multiple systems that are moving at different (but constant) velocities.
Relativity without the second postulate
From the principle of relativity alone without assuming the constancy of the speed of light (i.e., using the isotropy of space and the symmetry implied by the principle of special relativity) it can be shown that the spacetime transformations between inertial frames are either Euclidean, Galilean, or Lorentzian. In the Lorentzian case, one can then obtain relativistic interval conservation and a certain finite limiting speed. Experiments suggest that this speed is the speed of light in a vacuum.[p 8][19]
Lorentz invariance as the essential core of special relativity
Alternative approaches to special relativity
Einstein consistently based the derivation of Lorentz invariance (the essential core of special relativity) on just the two basic principles of relativity and light-speed invariance. He wrote:
The insight fundamental for the special theory of relativity is this: The assumptions relativity and light speed invariance are compatible if relations of a new type ("Lorentz transformation") are postulated for the conversion of coordinates and times of events ... The universal principle of the special theory of relativity is contained in the postulate: The laws of physics are invariant with respect to Lorentz transformations (for the transition from one inertial system to any other arbitrarily chosen inertial system). This is a restricting principle for natural laws ...[p 5]
Thus many modern treatments of special relativity base it on the single postulate of universal Lorentz covariance, or, equivalently, on the single postulate of Minkowski spacetime.[p 9][p 10]
Rather than considering universal Lorentz covariance to be a derived principle, this article considers it to be the fundamental postulate of special relativity. The traditional two-postulate approach to special relativity is presented in innumerable college textbooks and popular presentations.[20] Textbooks starting with the single postulate of Minkowski spacetime include those by Taylor and Wheeler[21] and by Callahan.[22] This is also the approach followed by the Wikipedia articles Spacetime and Minkowski diagram.
Lorentz transformation and its inverse
Define an event to have spacetime coordinates (t, x, y, z) in system S and (t′, x′, y′, z′) in a reference frame moving at a velocity v with respect to that frame, S′. Then the Lorentz transformation specifies that these coordinates are related in the following way: [math]\displaystyle{ \begin{align} t' &= \gamma \ (t - vx/c^2) \\ x' &= \gamma \ (x - v t) \\ y' &= y \\ z' &= z , \end{align} }[/math] where [math]\displaystyle{ \gamma = \frac{1}{\sqrt{1 - v^2/c^2}} }[/math] is the Lorentz factor and c is the speed of light in vacuum, and the velocity v of S′, relative to S, is parallel to the x-axis. For simplicity, the y and z coordinates are unaffected; only the x and t coordinates are transformed. These Lorentz transformations form a one-parameter group of linear mappings, that parameter being called rapidity.
Solving the four transformation equations above for the unprimed coordinates yields the inverse Lorentz transformation: [math]\displaystyle{ \begin{align} t &= \gamma ( t' + v x'/c^2) \\ x &= \gamma ( x' + v t') \\ y &= y' \\ z &= z'. \end{align} }[/math]
This shows that the unprimed frame is moving with the velocity −v, as measured in the primed frame.[23]
There is nothing special about the x-axis. The transformation can apply to the y- or z-axis, or indeed in any direction parallel to the motion (which are warped by the γ factor) and perpendicular; see the article Lorentz transformation for details.
A quantity invariant under Lorentz transformations is known as a Lorentz scalar.
Writing the Lorentz transformation and its inverse in terms of coordinate differences, where one event has coordinates (x1, t1) and (x′1, t′1), another event has coordinates (x2, t2) and (x′2, t′2), and the differences are defined as
- [math]\displaystyle{ \Delta x' = x'_2-x'_1 \ , \ \Delta t' = t'_2-t'_1 \ . }[/math]
- [math]\displaystyle{ \Delta x = x_2-x_1 \ , \ \ \Delta t = t_2-t_1 \ . }[/math]
we get
- [math]\displaystyle{ \Delta x' = \gamma \ (\Delta x - v \,\Delta t) \ ,\ \ }[/math] [math]\displaystyle{ \Delta t' = \gamma \ \left(\Delta t - v \ \Delta x / c^{2} \right) \ . }[/math]
- [math]\displaystyle{ \Delta x = \gamma \ (\Delta x' + v \,\Delta t') \ , \ }[/math] [math]\displaystyle{ \Delta t = \gamma \ \left(\Delta t' + v \ \Delta x' / c^{2} \right) \ . }[/math]
If we take differentials instead of taking differences, we get
- [math]\displaystyle{ dx' = \gamma \ (dx - v\,dt) \ ,\ \ }[/math] [math]\displaystyle{ dt' = \gamma \ \left( dt - v \ dx / c^{2} \right) \ . }[/math]
- [math]\displaystyle{ dx = \gamma \ (dx' + v\,dt') \ , \ }[/math] [math]\displaystyle{ dt = \gamma \ \left(dt' + v \ dx' / c^{2} \right) \ . }[/math]
Graphical representation of the Lorentz transformation
Spacetime diagrams (Minkowski diagrams) are an extremely useful aid to visualizing how coordinates transform between different reference frames. Although it is not as easy to perform exact computations using them as directly invoking the Lorentz transformations, their main power is their ability to provide an intuitive grasp of the results of a relativistic scenario.[19]
To draw a spacetime diagram, begin by considering two Galilean reference frames, S and S', in standard configuration, as shown in Fig. 2-1.[19][24]:155–199
Fig. 3-1a. Draw the [math]\displaystyle{ x }[/math] and [math]\displaystyle{ t }[/math] axes of frame S. The [math]\displaystyle{ x }[/math] axis is horizontal and the [math]\displaystyle{ t }[/math] (actually [math]\displaystyle{ ct }[/math]) axis is vertical, which is the opposite of the usual convention in kinematics. The [math]\displaystyle{ ct }[/math] axis is scaled by a factor of [math]\displaystyle{ c }[/math] so that both axes have common units of length. In the diagram shown, the gridlines are spaced one unit distance apart. The 45° diagonal lines represent the worldlines of two photons passing through the origin at time [math]\displaystyle{ t = 0. }[/math] The slope of these worldlines is 1 because the photons advance one unit in space per unit of time. Two events, [math]\displaystyle{ \text{A} }[/math] and [math]\displaystyle{ \text{B}, }[/math] have been plotted on this graph so that their coordinates may be compared in the S and S' frames.
Fig. 3-1b. Draw the [math]\displaystyle{ x' }[/math] and [math]\displaystyle{ ct' }[/math] axes of frame S'. The [math]\displaystyle{ ct' }[/math] axis represents the worldline of the origin of the S' coordinate system as measured in frame S. In this figure, [math]\displaystyle{ v = c/2. }[/math] Both the [math]\displaystyle{ ct' }[/math] and [math]\displaystyle{ x' }[/math] axes are tilted from the unprimed axes by an angle [math]\displaystyle{ \alpha = \tan^{-1}(\beta), }[/math] where [math]\displaystyle{ \beta = v/c. }[/math] The primed and unprimed axes share a common origin because frames S and S' had been set up in standard configuration, so that [math]\displaystyle{ t=0 }[/math] when [math]\displaystyle{ t'=0. }[/math]
Fig. 3-1c. Units in the primed axes have a different scale from units in the unprimed axes. From the Lorentz transformations, we observe that [math]\displaystyle{ (x', ct') }[/math] coordinates of [math]\displaystyle{ (0, 1) }[/math] in the primed coordinate system transform to [math]\displaystyle{ (\beta \gamma, \gamma) }[/math] in the unprimed coordinate system. Likewise, [math]\displaystyle{ (x', ct') }[/math] coordinates of [math]\displaystyle{ (1, 0) }[/math] in the primed coordinate system transform to [math]\displaystyle{ (\gamma, \beta \gamma) }[/math] in the unprimed system. Draw gridlines parallel with the [math]\displaystyle{ ct' }[/math] axis through points [math]\displaystyle{ (k \gamma, k \beta \gamma) }[/math] as measured in the unprimed frame, where [math]\displaystyle{ k }[/math] is an integer. Likewise, draw gridlines parallel with the [math]\displaystyle{ x' }[/math] axis through [math]\displaystyle{ (k \beta \gamma, k \gamma) }[/math] as measured in the unprimed frame. Using the Pythagorean theorem, we observe that the spacing between [math]\displaystyle{ ct' }[/math] units equals [math]\displaystyle{ \sqrt{(1 + \beta ^2)/(1 - \beta ^2)} }[/math] times the spacing between [math]\displaystyle{ ct }[/math] units, as measured in frame S. This ratio is always greater than 1, and ultimately it approaches infinity as [math]\displaystyle{ \beta \to 1. }[/math]
Fig. 3-1d. Since the speed of light is an invariant, the worldlines of two photons passing through the origin at time [math]\displaystyle{ t' = 0 }[/math] still plot as 45° diagonal lines. The primed coordinates of [math]\displaystyle{ \text{A} }[/math] and [math]\displaystyle{ \text{B} }[/math] are related to the unprimed coordinates through the Lorentz transformations and could be approximately measured from the graph (assuming that it has been plotted accurately enough), but the real merit of a Minkowski diagram is its granting us a geometric view of the scenario. For example, in this figure, we observe that the two timelike-separated events that had different x-coordinates in the unprimed frame are now at the same position in space.
While the unprimed frame is drawn with space and time axes that meet at right angles, the primed frame is drawn with axes that meet at acute or obtuse angles. This asymmetry is due to unavoidable distortions in how spacetime coordinates map onto a Cartesian plane, but the frames are actually equivalent.
Consequences derived from the Lorentz transformation
The consequences of special relativity can be derived from the Lorentz transformation equations.[25] These transformations, and hence special relativity, lead to different physical predictions than those of Newtonian mechanics at all relative velocities, and most pronounced when relative velocities become comparable to the speed of light. The speed of light is so much larger than anything most humans encounter that some of the effects predicted by relativity are initially counterintuitive.
Invariant interval
In Galilean relativity, an object's length ([math]\displaystyle{ \Delta r }[/math])[note 3] and the temporal separation between two events ([math]\displaystyle{ \Delta t }[/math]) are independent invariants, the values of which do not change when observed from different frames of reference.[note 4][note 5]
In special relativity, however, the interweaving of spatial and temporal coordinates generates the concept of an invariant interval, denoted as [math]\displaystyle{ \Delta s^2 }[/math]:[note 6] [math]\displaystyle{ \Delta s^2 \; \overset\text{def}{=} \; c^2 \Delta t^2 - (\Delta x^2 + \Delta y^2 + \Delta z^2) }[/math]
The interweaving of space and time revokes the implicitly assumed concepts of absolute simultaneity and synchronization across non-comoving frames.
The form of [math]\displaystyle{ \Delta s^2 , }[/math] being the difference of the squared time lapse and the squared spatial distance, demonstrates a fundamental discrepancy between Euclidean and spacetime distances.[note 7] The invariance of this interval is a property of the general Lorentz transform (also called the Poincaré transformation), making it an isometry of spacetime. The general Lorentz transform extends the standard Lorentz transform (which deals with translations without rotation, that is, Lorentz boosts, in the x-direction) with all other translations, reflections, and rotations between any Cartesian inertial frame.[29]:33–34
In the analysis of simplified scenarios, such as spacetime diagrams, a reduced-dimensionality form of the invariant interval is often employed: [math]\displaystyle{ \Delta s^2 \, = \, c^2 \Delta t^2 - \Delta x^2 }[/math]
Demonstrating that the interval is invariant is straightforward for the reduced-dimensionality case and with frames in standard configuration:[19] [math]\displaystyle{ \begin{align} c^2 \Delta t^2 - \Delta x^2 &= c^2 \gamma ^2 \left(\Delta t' + \dfrac{v \Delta x'}{c^2} \right)^2 - \gamma ^2 \ (\Delta x' + v \Delta t')^2 \\ &= \gamma ^2 \left( c^2 \Delta t' ^ {\, 2} + 2 v \Delta x' \Delta t' + \dfrac{v^2 \Delta x' ^ {\, 2}}{c^2} \right) - \gamma ^2 \ (\Delta x' ^ {\, 2} + 2 v \Delta x' \Delta t' + v^2 \Delta t' ^ {\, 2}) \\ &= \gamma ^2 c^2 \Delta t' ^ {\, 2} - \gamma ^2 v^2 \Delta t' ^{\, 2} - \gamma ^2 \Delta x' ^ {\, 2} + \gamma ^2 \dfrac{v^2 \Delta x' ^ {\, 2}}{c^2} \\ &= \gamma ^2 c^2 \Delta t' ^ {\, 2} \left( 1 - \dfrac{v^2}{c^2} \right) - \gamma ^2 \Delta x' ^{\, 2} \left( 1 - \dfrac{v^2}{c^2} \right) \\ &= c^2 \Delta t' ^{\, 2} - \Delta x' ^{\, 2} \end{align} }[/math]
The value of [math]\displaystyle{ \Delta s^2 }[/math] is hence independent of the frame in which it is measured.
In considering the physical significance of [math]\displaystyle{ \Delta s^2 }[/math], there are three cases to note:[19][30]:25–39
- Δs2 > 0: In this case, the two events are separated by more time than space, and they are hence said to be timelike separated. This implies that [math]\displaystyle{ | \Delta x / \Delta t | \lt c , }[/math] and given the Lorentz transformation [math]\displaystyle{ \Delta x' = \gamma \ (\Delta x - v \,\Delta t) , }[/math] it is evident that there exists a [math]\displaystyle{ v }[/math] less than [math]\displaystyle{ c }[/math] for which [math]\displaystyle{ \Delta x' = 0 }[/math] (in particular, [math]\displaystyle{ v = \Delta x / \Delta t }[/math]). In other words, given two events that are timelike separated, it is possible to find a frame in which the two events happen at the same place. In this frame, the separation in time, [math]\displaystyle{ \Delta s / c, }[/math] is called the proper time.
- Δs2 < 0: In this case, the two events are separated by more space than time, and they are hence said to be spacelike separated. This implies that [math]\displaystyle{ | \Delta x / \Delta t | \gt c , }[/math] and given the Lorentz transformation [math]\displaystyle{ \Delta t' = \gamma \ (\Delta t - v \Delta x / c^2) , }[/math] there exists a [math]\displaystyle{ v }[/math] less than [math]\displaystyle{ c }[/math] for which [math]\displaystyle{ \Delta t' = 0 }[/math] (in particular, [math]\displaystyle{ v = c^2 \Delta t / \Delta x }[/math]). In other words, given two events that are spacelike separated, it is possible to find a frame in which the two events happen at the same time. In this frame, the separation in space, [math]\displaystyle{ \sqrt { - \Delta s^2 }, }[/math] is called the proper distance, or proper length. For values of [math]\displaystyle{ v }[/math] greater than and less than [math]\displaystyle{ c^2 \Delta t / \Delta x , }[/math] the sign of [math]\displaystyle{ \Delta t' }[/math] changes, meaning that the temporal order of spacelike-separated events changes depending on the frame in which the events are viewed. But the temporal order of timelike-separated events is absolute, since the only way that [math]\displaystyle{ v }[/math] could be greater than [math]\displaystyle{ c^2 \Delta t / \Delta x }[/math] would be if [math]\displaystyle{ v \gt c. }[/math]
- Δs2 = 0: In this case, the two events are said to be lightlike separated. This implies that [math]\displaystyle{ | \Delta x / \Delta t | = c , }[/math] and this relationship is frame independent due to the invariance of [math]\displaystyle{ s^2 . }[/math] From this, we observe that the speed of light is [math]\displaystyle{ c }[/math] in every inertial frame. In other words, starting from the assumption of universal Lorentz covariance, the constant speed of light is a derived result, rather than a postulate as in the two-postulates formulation of the special theory.
Relativity of simultaneity

Consider two events happening in two different locations that occur simultaneously in the reference frame of one inertial observer. They may occur non-simultaneously in the reference frame of another inertial observer (lack of absolute simultaneity).
From Equation 3 (the forward Lorentz transformation in terms of coordinate differences) [math]\displaystyle{ \Delta t' = \gamma \left(\Delta t - \frac{v \,\Delta x}{c^{2}} \right) }[/math]
It is clear that the two events that are simultaneous in frame S (satisfying Δt = 0), are not necessarily simultaneous in another inertial frame S′ (satisfying Δt′ = 0). Only if these events are additionally co-local in frame S (satisfying Δx = 0), will they be simultaneous in another frame S′.
The Sagnac effect can be considered a manifestation of the relativity of simultaneity.[31] Since relativity of simultaneity is a first order effect in [math]\displaystyle{ v }[/math],[19] instruments based on the Sagnac effect for their operation, such as ring laser gyroscopes and fiber optic gyroscopes, are capable of extreme levels of sensitivity.[p 14]
Time dilation
The time lapse between two events is not invariant from one observer to another, but is dependent on the relative speeds of the observers' reference frames.
Suppose a clock is at rest in the unprimed system S. The location of the clock on two different ticks is then characterized by Δx = 0. To find the relation between the times between these ticks as measured in both systems, Equation 3 can be used to find:
- [math]\displaystyle{ \Delta t' = \gamma\, \Delta t }[/math] for events satisfying [math]\displaystyle{ \Delta x = 0 \ . }[/math]
This shows that the time (Δt′) between the two ticks as seen in the frame in which the clock is moving (S′), is longer than the time (Δt) between these ticks as measured in the rest frame of the clock (S). Time dilation explains a number of physical phenomena; for example, the lifetime of high speed muons created by the collision of cosmic rays with particles in the Earth's outer atmosphere and moving towards the surface is greater than the lifetime of slowly moving muons, created and decaying in a laboratory.[32]
Whenever one hears a statement to the effect that "moving clocks run slow", one should envision an inertial reference frame thickly populated with identical, synchronized clocks. As a moving clock travels through this array, its reading at any particular point is compared with a stationary clock at the same point.[33]:149-152
The measurements that we would get if we actually looked at a moving clock would, in general, not at all be the same thing, because the time that would see would be delayed by the finite speed of light, i.e the times that we see would be distorted by the Doppler effect. Measurements of relativistic effects must always be understood as having been made after finite speed-of-light effects have been factored out.[33]:149-152
Langevin's light-clock
Paul Langevin, an early proponent of the theory of relativity, did much to popularize the theory in the face of resistance by many physicists to Einstein's revolutionary concepts. Among his numerous contributions to the foundations of special relativity were independent work on the mass-energy relationship, a thorough examination of the twin paradox, and investigations into rotating coordinate systems. His name is frequently attached to a hypothetical construct called a "light-clock" (originally developed by Lewis and Tolman in 1909[34]) which he used to perform a novel derivation of the Lorentz transformation.[35]
A light-clock is imagined to be a box of perfectly reflecting walls wherein a light signal reflects back and forth from opposite faces. The concept of time dilation is frequently taught using a light-clock that is traveling in uniform inertial motion perpendicular to a line connecting the two mirrors.[36][37][38][39] (Langevin himself made use of a light-clock oriented parallel to its line of motion.[35])
Consider the scenario illustrated in Fig. 4-3A. Observer A holds a light-clock of length [math]\displaystyle{ L }[/math] as well as an electronic timer with which she measures how long it takes a pulse to make a round trip up and down along the light-clock. Although observer A is traveling rapidly along a train, from her point of view the emission and receipt of the pulse occur at the same place, and she measures the interval using a single clock located at the precise position of these two events. For the interval between these two events, observer A finds [math]\displaystyle{ t_A = 2 L/c. }[/math] A time interval measured using a single clock which is motionless in a particular reference frame is called a proper time interval.[40]
Fig. 4-3B illustrates these same two events from the standpoint of observer B, who is parked by the tracks as the train goes by at a speed of [math]\displaystyle{ v. }[/math] Instead of making straight up-and-down motions, observer B sees the pulses moving along a zig-zag line. However, because of the postulate of the constancy of the speed of light, the speed of the pulses along these diagonal lines is the same [math]\displaystyle{ c }[/math] that observer A saw for her up-and-down pulses. B measures the speed of the vertical component of these pulses as [math]\displaystyle{ \pm \sqrt{c^2 - v^2}, }[/math] so that the total round-trip time of the pulses is [math]\displaystyle{ t_B = 2L \big/ \sqrt{ c^2 - v^2 } = {} }[/math][math]\displaystyle{ t_A \big/ \sqrt {1 - v^2 / c^2} . }[/math] Note that for observer B, the emission and receipt of the light pulse occurred at different places, and he measured the interval using two stationary and synchronized clocks located at two different positions in his reference frame. The interval that B measured was therefore not a proper time interval because he did not measure it with a single resting clock.[40]
Reciprocal time dilation
In the above description of the Langevin light-clock, the labeling of one observer as stationary and the other as in motion was completely arbitrary. One could just as well have observer B carrying the light-clock and moving at a speed of [math]\displaystyle{ v }[/math] to the left, in which case observer A would perceive B's clock as running slower than her local clock.
There is no paradox here, because there is no independent observer C who will agree with both A and B. Observer C necessarily makes his measurements from his own reference frame. If that reference frame coincides with A's reference frame, then C will agree with A's measurement of time. If C's reference frame coincides with B's reference frame, then C will agree with B's measurement of time. If C's reference frame coincides with neither A's frame nor B's frame, then C's measurement of time will disagree with both A's and B's measurement of time.[41]
Twin paradox
The reciprocity of time dilation between two observers in separate inertial frames leads to the so-called twin paradox, articulated in its present form by Langevin in 1911.[42] Langevin imagined an adventurer wishing to explore the future of the Earth. This traveler boards a projectile capable of traveling at 99.995% of the speed of light. After making a round-trip journey to and from a nearby star lasting only two years of his own life, he returns to an Earth that is two hundred years older.
This result appears puzzling because both the traveler and an Earthbound observer would see the other as moving, and so, because of the reciprocity of time dilation, one might initially expect that each should have found the other to have aged less. In reality, there is no paradox at all, because in order for the two observers to compare their proper times, the symmetry of the situation must be broken: At least one of the two observers must change their state of motion to match that of the other.[43]
Knowing the general resolution of the paradox, however, does not immediately yield the ability to calculate correct quantitative results. Many solutions to this puzzle have been provided in the literature and have been reviewed in the Twin paradox article. We will examine in the following one such solution to the paradox.
Our basic aim will be to demonstrate that, after the trip, both twins are in perfect agreement about who aged by how much, regardless of their different experiences. Fig 4-4 illustrates a scenario where the traveling twin flies at 0.6 c to and from a star 3 ly distant. During the trip, each twin sends yearly time signals (measured in their own proper times) to the other. After the trip, the cumulative counts are compared. On the outward phase of the trip, each twin receives the other's signals at the lowered rate of [math]\displaystyle{ f' = f \sqrt{(1-\beta)/(1+\beta)}. }[/math] Initially, the situation is perfectly symmetric: note that each twin receives the other's one-year signal at two years measured on their own clock. The symmetry is broken when the traveling twin turns around at the four-year mark as measured by her clock. During the remaining four years of her trip, she receives signals at the enhanced rate of [math]\displaystyle{ f'' =f \sqrt{(1+\beta)/(1-\beta)}. }[/math] The situation is quite different with the stationary twin. Because of light-speed delay, he does not see his sister turn around until eight years have passed on his own clock. Thus, he receives enhanced-rate signals from his sister for only a relatively brief period. Although the twins disagree in their respective measures of total time, we see in the following table, as well as by simple observation of the Minkowski diagram, that each twin is in total agreement with the other as to the total number of signals sent from one to the other. There is hence no paradox.[33]:152-159
| Item | Measured by the stay-at-home |
Fig 4-4 | Measured by the traveler |
Fig 4-4 |
|---|---|---|---|---|
| Total time of trip | [math]\displaystyle{ T = \frac{2L}{v} }[/math] | 10 yr | [math]\displaystyle{ T' = \frac{2L}{\gamma v} }[/math] | 8 yr |
| Total number of pulses sent | [math]\displaystyle{ fT = \frac{2fL}{v} }[/math] | 10 | [math]\displaystyle{ fT' = \frac{2fL}{\gamma v} }[/math] | 8 |
| Time when traveler's turnaround is detected | [math]\displaystyle{ t_1 = \frac{L}{v} + \frac{L}{c} }[/math] | 8 yr | [math]\displaystyle{ t_1' = \frac{L}{\gamma v} }[/math] | 4 yr |
| Number of pulses received at initial [math]\displaystyle{ f' }[/math] rate | [math]\displaystyle{ f't_1 }[/math] [math]\displaystyle{ = \frac{fL}{v}(1 + \beta)\left(\frac{1-\beta}{1+\beta}\right)^{1/2} }[/math] [math]\displaystyle{ = \frac{fL}{v}(1 - \beta ^2)^{1/2} }[/math] |
4 | [math]\displaystyle{ f't_1' }[/math] [math]\displaystyle{ = \frac{fL}{v}(1 - \beta^2)^{1/2}\left(\frac{1-\beta}{1+\beta}\right)^{1/2} }[/math] [math]\displaystyle{ = \frac{fL}{v}(1 - \beta ) }[/math] |
2 |
| Time for remainder of trip | [math]\displaystyle{ t_2 = \frac{L}{v} - \frac{L}{c} }[/math] | 2 yr | [math]\displaystyle{ t_2' = \frac{L}{\gamma v} }[/math] | 4 yr |
| Number of signals received at final [math]\displaystyle{ f'' }[/math] rate | [math]\displaystyle{ f''t_2 }[/math] [math]\displaystyle{ = \frac{fL}{v}(1 - \beta)\left( \frac{1 + \beta}{1 - \beta} \right)^{1/2} }[/math] [math]\displaystyle{ = \frac{fL}{v}(1 - \beta ^2)^{1/2} }[/math] | 4 | [math]\displaystyle{ f''t_2' }[/math] [math]\displaystyle{ = \frac{fL}{v}(1 - \beta^2)^{1/2}\left( \frac{1 + \beta}{1 - \beta} \right)^{1/2} }[/math] [math]\displaystyle{ = \frac{fL}{v}(1 + \beta) }[/math] | 8 |
| Total number of received pulses | [math]\displaystyle{ \frac{2fL}{v}(1 - \beta ^2)^{1/2} }[/math] [math]\displaystyle{ = \frac{2fL}{\gamma v} }[/math] | 8 | [math]\displaystyle{ \frac{2fL}{v} }[/math] | 10 |
| Twin's calculation as to how much the other twin should have aged | [math]\displaystyle{ T' = \frac{2L}{\gamma v} }[/math] | 8 yr | [math]\displaystyle{ T = \frac{2L}{v} }[/math] | 10 yr |
Length contraction
The dimensions (e.g., length) of an object as measured by one observer may be smaller than the results of measurements of the same object made by another observer (e.g., the ladder paradox involves a long ladder traveling near the speed of light and being contained within a smaller garage).
Similarly, suppose a measuring rod is at rest and aligned along the x-axis in the unprimed system S. In this system, the length of this rod is written as Δx. To measure the length of this rod in the system S′, in which the rod is moving, the distances x′ to the end points of the rod must be measured simultaneously in that system S′. In other words, the measurement is characterized by Δt′ = 0, which can be combined with Equation 4 to find the relation between the lengths Δx and Δx′:
- [math]\displaystyle{ \Delta x' = \frac{\Delta x}{\gamma} }[/math] for events satisfying [math]\displaystyle{ \Delta t' = 0 \ . }[/math]
This shows that the length (Δx′) of the rod as measured in the frame in which it is moving (S′), is shorter than its length (Δx) in its own rest frame (S).
Time dilation and length contraction are not merely appearances. Time dilation is explicitly related to our way of measuring time intervals between events that occur at the same place in a given coordinate system (called "co-local" events). These time intervals (which can be, and are, actually measured experimentally by relevant observers) are different in another coordinate system moving with respect to the first, unless the events, in addition to being co-local, are also simultaneous. Similarly, length contraction relates to our measured distances between separated but simultaneous events in a given coordinate system of choice. If these events are not co-local, but are separated by distance (space), they will not occur at the same spatial distance from each other when seen from another moving coordinate system.
Lorentz transformation of velocities
Consider two frames S and S′ in standard configuration. A particle in S moves in the x direction with velocity vector [math]\displaystyle{ \mathbf{u}. }[/math] What is its velocity [math]\displaystyle{ \mathbf{u'} }[/math] in frame S′ ?
We can write
[math]\displaystyle{ \mathbf{|u|} = u = dx / dt \, . }[/math] |
|
() |
[math]\displaystyle{ \mathbf{|u'|} = u' = dx' / dt' \, . }[/math] |
|
() |
Substituting expressions for [math]\displaystyle{ dx' }[/math] and [math]\displaystyle{ dt' }[/math] from Equation 5 into Equation 8, followed by straightforward mathematical manipulations and back-substitution from Equation 7 yields the Lorentz transformation of the speed [math]\displaystyle{ u }[/math] to [math]\displaystyle{ u' }[/math]:
[math]\displaystyle{ u' = \frac{dx'}{dt'}=\frac{\gamma(dx-v\,dt)}{\gamma \left(dt-\dfrac{v\,dx}{c^2} \right)} = \frac{\dfrac{dx}{dt}-v}{1 - \dfrac{v}{c^2} \, \dfrac{dx}{dt} } =\frac{u-v}{1- \dfrac{uv}{c^2}}. }[/math] |
|
() |
The inverse relation is obtained by interchanging the primed and unprimed symbols and replacing [math]\displaystyle{ v }[/math] with [math]\displaystyle{ -v \ . }[/math]
[math]\displaystyle{ u=\frac{u'+v}{1+ u'v / c^2}. }[/math] |
|
() |
For [math]\displaystyle{ \mathbf{u} }[/math] not aligned along the x-axis, we write:[12]:47–49
[math]\displaystyle{ \mathbf{u} = (u_1, \ u_2,\ u_3 ) = ( dx / dt, \ dy/dt, \ dz/dt) \ . }[/math] |
|
() |
[math]\displaystyle{ \mathbf{u'} = (u_1', \ u_2', \ u_3') = ( dx' / dt', \ dy'/dt', \ dz'/dt') \ . }[/math] |
|
() |
The forward and inverse transformations for this case are:
[math]\displaystyle{ u_1'=\frac{u_1 -v}{1-u_1 v / c^2 } \ , \qquad u_2'=\frac{u_2}{\gamma \left( 1-u_1 v / c^2 \right) } \ , \qquad u_3'=\frac{u_3}{\gamma \left( 1- u_1 v / c^2 \right) } \ . }[/math] |
|
() |
[math]\displaystyle{ u_1=\frac{u_1' +v}{1+ u_1' v / c^2 } \ , \qquad u_2=\frac{u_2'}{ \gamma \left( 1+ u_1' v / c^2 \right) } \ , \qquad u_3=\frac{u_3'}{\gamma \left( 1+ u_1' v / c^2 \right)} \ . }[/math] |
|
() |
Equation 10 and Equation 14 can be interpreted as giving the resultant [math]\displaystyle{ \mathbf{u} }[/math] of the two velocities [math]\displaystyle{ \mathbf{v} }[/math] and [math]\displaystyle{ \mathbf{u'}, }[/math] and they replace the formula [math]\displaystyle{ \mathbf{u = u' + v} }[/math] which is valid in Galilean relativity. Interpreted in such a fashion, they are commonly referred to as the relativistic velocity addition (or composition) formulas, valid for the three axes of S and S′ being aligned with each other (although not necessarily in standard configuration).[12]:47–49
We note the following points:
- If an object (e.g., a photon) were moving at the speed of light in one frame (i.e., u = ±c or u′ = ±c), then it would also be moving at the speed of light in any other frame, moving at |v| < c.
- The resultant speed of two velocities with magnitude less than c is always a velocity with magnitude less than c.
- If both |u| and |v| (and then also |u′| and |v′|) are small with respect to the speed of light (that is, e.g., |u/c| ≪ 1), then the intuitive Galilean transformations are recovered from the transformation equations for special relativity
- Attaching a frame to a photon (riding a light beam like Einstein considers) requires special treatment of the transformations.
There is nothing special about the x direction in the standard configuration. The above formalism applies to any direction; and three orthogonal directions allow dealing with all directions in space by decomposing the velocity vectors to their components in these directions. See Velocity-addition formula for details.
Thomas rotation
The composition of two non-collinear Lorentz boosts (i.e., two non-collinear Lorentz transformations, neither of which involve rotation) results in a Lorentz transformation that is not a pure boost but is the composition of a boost and a rotation.
Thomas rotation results from the relativity of simultaneity. In Fig. 4-5a, a rod of length [math]\displaystyle{ L }[/math] in its rest frame (i.e., having a proper length of [math]\displaystyle{ L }[/math]) rises vertically along the y-axis in the ground frame.
In Fig. 4-5b, the same rod is observed from the frame of a rocket moving at speed [math]\displaystyle{ v }[/math] to the right. If we imagine two clocks situated at the left and right ends of the rod that are synchronized in the frame of the rod, relativity of simultaneity causes the observer in the rocket frame to observe (not see) the clock at the right end of the rod as being advanced in time by [math]\displaystyle{ Lv/c^2 , }[/math] and the rod is correspondingly observed as tilted.[30]:98–99
Unlike second-order relativistic effects such as length contraction or time dilation, this effect becomes quite significant even at fairly low velocities. For example, this can be seen in the spin of moving particles, where Thomas precession is a relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope, relating the angular velocity of the spin of a particle following a curvilinear orbit to the angular velocity of the orbital motion.[30]:169–174
Thomas rotation provides the resolution to the well-known "meter stick and hole paradox".[p 15][30]:98–99
Causality and prohibition of motion faster than light
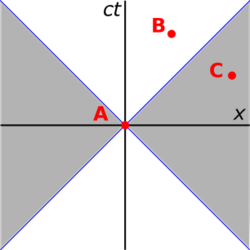
In Fig. 4-6, the time interval between the events A (the "cause") and B (the "effect") is 'time-like'; that is, there is a frame of reference in which events A and B occur at the same location in space, separated only by occurring at different times. If A precedes B in that frame, then A precedes B in all frames accessible by a Lorentz transformation. It is possible for matter (or information) to travel (below light speed) from the location of A, starting at the time of A, to the location of B, arriving at the time of B, so there can be a causal relationship (with A the cause and B the effect).
The interval AC in the diagram is 'space-like'; that is, there is a frame of reference in which events A and C occur simultaneously, separated only in space. There are also frames in which A precedes C (as shown) and frames in which C precedes A. But no frames are accessible by a Lorentz transformation, in which events A and C occur at the same location. If it were possible for a cause-and-effect relationship to exist between events A and C, paradoxes of causality would result.
For example, if signals could be sent faster than light, then signals could be sent into the sender's past (observer B in the diagrams).[44][p 16] A variety of causal paradoxes could then be constructed.
Consider the spacetime diagrams in Fig. 4-7. A and B stand alongside a railroad track, when a high-speed train passes by, with C riding in the last car of the train and D riding in the leading car. The world lines of A and B are vertical (ct), distinguishing the stationary position of these observers on the ground, while the world lines of C and D are tilted forwards (ct′), reflecting the rapid motion of the observers C and D stationary in their train, as observed from the ground.
- Fig. 4-7a. The event of "B passing a message to D", as the leading car passes by, is at the origin of D's frame. D sends the message along the train to C in the rear car, using a fictitious "instantaneous communicator". The worldline of this message is the fat red arrow along the [math]\displaystyle{ -x' }[/math] axis, which is a line of simultaneity in the primed frames of C and D. In the (unprimed) ground frame the signal arrives earlier than it was sent.
- Fig. 4-7b. The event of "C passing the message to A", who is standing by the railroad tracks, is at the origin of their frames. Now A sends the message along the tracks to B via an "instantaneous communicator". The worldline of this message is the blue fat arrow, along the [math]\displaystyle{ +x }[/math] axis, which is a line of simultaneity for the frames of A and B. As seen from the spacetime diagram, B will receive the message before having sent it out, a violation of causality.[45]
It is not necessary for signals to be instantaneous to violate causality. Even if the signal from D to C were slightly shallower than the [math]\displaystyle{ x' }[/math] axis (and the signal from A to B slightly steeper than the [math]\displaystyle{ x }[/math] axis), it would still be possible for B to receive his message before he had sent it. By increasing the speed of the train to near light speeds, the [math]\displaystyle{ ct' }[/math] and [math]\displaystyle{ x' }[/math] axes can be squeezed very close to the dashed line representing the speed of light. With this modified setup, it can be demonstrated that even signals only slightly faster than the speed of light will result in causality violation.[46]
Therefore, if causality is to be preserved, one of the consequences of special relativity is that no information signal or material object can travel faster than light in vacuum.
This is not to say that all faster than light speeds are impossible. Various trivial situations can be described where some "things" (not actual matter or energy) move faster than light.[47] For example, the location where the beam of a search light hits the bottom of a cloud can move faster than light when the search light is turned rapidly (although this does not violate causality or any other relativistic phenomenon).[48][49]
Optical effects
Dragging effects
In 1850, Hippolyte Fizeau and Léon Foucault independently established that light travels more slowly in water than in air, thus validating a prediction of Fresnel's wave theory of light and invalidating the corresponding prediction of Newton's corpuscular theory.[50] The speed of light was measured in still water. What would be the speed of light in flowing water?
In 1851, Fizeau conducted an experiment to answer this question, a simplified representation of which is illustrated in Fig. 5-1. A beam of light is divided by a beam splitter, and the split beams are passed in opposite directions through a tube of flowing water. They are recombined to form interference fringes, indicating a difference in optical path length, that an observer can view. The experiment demonstrated that dragging of the light by the flowing water caused a displacement of the fringes, showing that the motion of the water had affected the speed of the light.
According to the theories prevailing at the time, light traveling through a moving medium would be a simple sum of its speed through the medium plus the speed of the medium. Contrary to expectation, Fizeau found that although light appeared to be dragged by the water, the magnitude of the dragging was much lower than expected. If [math]\displaystyle{ u' = c/n }[/math] is the speed of light in still water, and [math]\displaystyle{ v }[/math] is the speed of the water, and [math]\displaystyle{ u_{\pm} }[/math] is the water-borne speed of light in the lab frame with the flow of water adding to or subtracting from the speed of light, then
[math]\displaystyle{ u_{\pm} =\frac{c}{n} \pm v\left(1-\frac{1}{n^2}\right) \ . }[/math]
Fizeau's results, although consistent with Fresnel's earlier hypothesis of partial aether dragging, were extremely disconcerting to physicists of the time. Among other things, the presence of an index of refraction term meant that, since [math]\displaystyle{ n }[/math] depends on wavelength, the aether must be capable of sustaining different motions at the same time.[note 8] A variety of theoretical explanations were proposed to explain Fresnel's dragging coefficient, that were completely at odds with each other. Even before the Michelson–Morley experiment, Fizeau's experimental results were among a number of observations that created a critical situation in explaining the optics of moving bodies.[51]
From the point of view of special relativity, Fizeau's result is nothing but an approximation to Equation 10, the relativistic formula for composition of velocities.[29]
- [math]\displaystyle{ u_{\pm} = \frac{u' \pm v}{ 1 \pm u'v/c^2 } = }[/math] [math]\displaystyle{ \frac {c/n \pm v}{ 1 \pm v/cn } \approx }[/math] [math]\displaystyle{ c \left( \frac{1}{n} \pm \frac{v}{c} \right) \left( 1 \mp \frac{v}{cn} \right) \approx }[/math] [math]\displaystyle{ \frac{c}{n} \pm v \left( 1 - \frac{1}{n^2} \right) }[/math]
Relativistic aberration of light
Because of the finite speed of light, if the relative motions of a source and receiver include a transverse component, then the direction from which light arrives at the receiver will be displaced from the geometric position in space of the source relative to the receiver. The classical calculation of the displacement takes two forms and makes different predictions depending on whether the receiver, the source, or both are in motion with respect to the medium. (1) If the receiver is in motion, the displacement would be the consequence of the aberration of light. The incident angle of the beam relative to the receiver would be calculable from the vector sum of the receiver's motions and the velocity of the incident light.[52] (2) If the source is in motion, the displacement would be the consequence of light-time correction. The displacement of the apparent position of the source from its geometric position would be the result of the source's motion during the time that its light takes to reach the receiver.[53]
The classical explanation failed experimental test. Since the aberration angle depends on the relationship between the velocity of the receiver and the speed of the incident light, passage of the incident light through a refractive medium should change the aberration angle. In 1810, Arago used this expected phenomenon in a failed attempt to measure the speed of light,[54] and in 1870, George Airy tested the hypothesis using a water-filled telescope, finding that, against expectation, the measured aberration was identical to the aberration measured with an air-filled telescope.[55] A "cumbrous" attempt to explain these results used the hypothesis of partial aether-drag,[56] but was incompatible with the results of the Michelson–Morley experiment, which apparently demanded complete aether-drag.[57]
Assuming inertial frames, the relativistic expression for the aberration of light is applicable to both the receiver moving and source moving cases. A variety of trigonometrically equivalent formulas have been published. Expressed in terms of the variables in Fig. 5-2, these include[29]:57–60
- [math]\displaystyle{ \cos \theta ' = \frac{ \cos \theta + v/c}{ 1 + (v/c)\cos \theta} }[/math] OR [math]\displaystyle{ \sin \theta ' = \frac{\sin \theta}{\gamma [ 1 + (v/c) \cos \theta ]} }[/math] OR [math]\displaystyle{ \tan \frac{\theta '}{2} = \left( \frac{c - v}{c + v} \right)^{1/2} \tan \frac {\theta}{2} }[/math]
Relativistic Doppler effect
Relativistic longitudinal Doppler effect
The classical Doppler effect depends on whether the source, receiver, or both are in motion with respect to the medium. The relativistic Doppler effect is independent of any medium. Nevertheless, relativistic Doppler shift for the longitudinal case, with source and receiver moving directly towards or away from each other, can be derived as if it were the classical phenomenon, but modified by the addition of a time dilation term, and that is the treatment described here.[58][59]
Assume the receiver and the source are moving away from each other with a relative speed [math]\displaystyle{ v\, }[/math] as measured by an observer on the receiver or the source (The sign convention adopted here is that [math]\displaystyle{ v }[/math] is negative if the receiver and the source are moving towards each other). Assume that the source is stationary in the medium. Then [math]\displaystyle{ f_{r} = \left(1 - \frac v {c_s} \right) f_s }[/math] where [math]\displaystyle{ c_s }[/math] is the speed of sound.
For light, and with the receiver moving at relativistic speeds, clocks on the receiver are time dilated relative to clocks at the source. The receiver will measure the received frequency to be [math]\displaystyle{ f_r = \gamma\left(1 - \beta\right) f_s = \sqrt{\frac{1 - \beta}{1 + \beta}}\,f_s. }[/math] where
- [math]\displaystyle{ \beta = v/c }[/math] and
- [math]\displaystyle{ \gamma = \frac{1}{\sqrt{1 - \beta^2}} }[/math] is the Lorentz factor.
An identical expression for relativistic Doppler shift is obtained when performing the analysis in the reference frame of the receiver with a moving source.[60][19]
Transverse Doppler effect
The transverse Doppler effect is one of the main novel predictions of the special theory of relativity.
Classically, one might expect that if source and receiver are moving transversely with respect to each other with no longitudinal component to their relative motions, that there should be no Doppler shift in the light arriving at the receiver.
Special relativity predicts otherwise. Fig. 5-3 illustrates two common variants of this scenario. Both variants can be analyzed using simple time dilation arguments.[19] In Fig. 5-3a, the receiver observes light from the source as being blueshifted by a factor of [math]\displaystyle{ \gamma }[/math]. In Fig. 5-3b, the light is redshifted by the same factor.
Measurement versus visual appearance
Time dilation and length contraction are not optical illusions, but genuine effects. Measurements of these effects are not an artifact of Doppler shift, nor are they the result of neglecting to take into account the time it takes light to travel from an event to an observer.
Scientists make a fundamental distinction between measurement or observation on the one hand, versus visual appearance, or what one sees. The measured shape of an object is a hypothetical snapshot of all of the object's points as they exist at a single moment in time. But the visual appearance of an object is affected by the varying lengths of time that light takes to travel from different points on the object to one's eye.
For many years, the distinction between the two had not been generally appreciated, and it had generally been thought that a length contracted object passing by an observer would in fact actually be seen as length contracted. In 1959, James Terrell and Roger Penrose independently pointed out that differential time lag effects in signals reaching the observer from the different parts of a moving object result in a fast moving object's visual appearance being quite different from its measured shape. For example, a receding object would appear contracted, an approaching object would appear elongated, and a passing object would have a skew appearance that has been likened to a rotation.[p 19][p 20][61][62] A sphere in motion retains the circular outline for all speeds, for any distance, and for all view angles, although the surface of the sphere and the images on it will appear distorted.[63][64]
Both Fig. 5-4 and Fig. 5-5 illustrate objects moving transversely to the line of sight. In Fig. 5-4, a cube is viewed from a distance of four times the length of its sides. At high speeds, the sides of the cube that are perpendicular to the direction of motion appear hyperbolic in shape. The cube is actually not rotated. Rather, light from the rear of the cube takes longer to reach one's eyes compared with light from the front, during which time the cube has moved to the right. At high speeds, the sphere in Fig. 5-5 takes on the appearance of a flattened disk tilted up to 45° from the line of sight. If the objects' motions are not strictly transverse but instead include a longitudinal component, exaggerated distortions in perspective may be seen.[65] This illusion has come to be known as Terrell rotation or the Terrell–Penrose effect.[note 9]
Another example where visual appearance is at odds with measurement comes from the observation of apparent superluminal motion in various radio galaxies, BL Lac objects, quasars, and other astronomical objects that eject relativistic-speed jets of matter at narrow angles with respect to the viewer. An apparent optical illusion results giving the appearance of faster than light travel.[66][67][68] In Fig. 5-6, galaxy M87 streams out a high-speed jet of subatomic particles almost directly towards us, but Penrose–Terrell rotation causes the jet to appear to be moving laterally in the same manner that the appearance of the cube in Fig. 5-4 has been stretched out.[69]
Dynamics
Section Consequences derived from the Lorentz transformation dealt strictly with kinematics, the study of the motion of points, bodies, and systems of bodies without considering the forces that caused the motion. This section discusses masses, forces, energy and so forth, and as such requires consideration of physical effects beyond those encompassed by the Lorentz transformation itself.
Equivalence of mass and energy
As an object's speed approaches the speed of light from an observer's point of view, its relativistic mass increases thereby making it more and more difficult to accelerate it from within the observer's frame of reference.
The energy content of an object at rest with mass m equals mc2. Conservation of energy implies that, in any reaction, a decrease of the sum of the masses of particles must be accompanied by an increase in kinetic energies of the particles after the reaction. Similarly, the mass of an object can be increased by taking in kinetic energies.
In addition to the papers referenced above—which give derivations of the Lorentz transformation and describe the foundations of special relativity—Einstein also wrote at least four papers giving heuristic arguments for the equivalence (and transmutability) of mass and energy, for E = mc2.
Mass–energy equivalence is a consequence of special relativity. The energy and momentum, which are separate in Newtonian mechanics, form a four-vector in relativity, and this relates the time component (the energy) to the space components (the momentum) in a non-trivial way. For an object at rest, the energy–momentum four-vector is (E/c, 0, 0, 0): it has a time component which is the energy, and three space components which are zero. By changing frames with a Lorentz transformation in the x direction with a small value of the velocity v, the energy momentum four-vector becomes (E/c, Ev/c2, 0, 0). The momentum is equal to the energy multiplied by the velocity divided by c2. As such, the Newtonian mass of an object, which is the ratio of the momentum to the velocity for slow velocities, is equal to E/c2.
The energy and momentum are properties of matter and radiation, and it is impossible to deduce that they form a four-vector just from the two basic postulates of special relativity by themselves, because these do not talk about matter or radiation, they only talk about space and time. The derivation therefore requires some additional physical reasoning. In his 1905 paper, Einstein used the additional principles that Newtonian mechanics should hold for slow velocities, so that there is one energy scalar and one three-vector momentum at slow velocities, and that the conservation law for energy and momentum is exactly true in relativity. Furthermore, he assumed that the energy of light is transformed by the same Doppler-shift factor as its frequency, which he had previously shown to be true based on Maxwell's equations.[p 1] The first of Einstein's papers on this subject was "Does the Inertia of a Body Depend upon its Energy Content?" in 1905.[p 21] Although Einstein's argument in this paper is nearly universally accepted by physicists as correct, even self-evident, many authors over the years have suggested that it is wrong.[70] Other authors suggest that the argument was merely inconclusive because it relied on some implicit assumptions.[71]
Einstein acknowledged the controversy over his derivation in his 1907 survey paper on special relativity. There he notes that it is problematic to rely on Maxwell's equations for the heuristic mass–energy argument. The argument in his 1905 paper can be carried out with the emission of any massless particles, but the Maxwell equations are implicitly used to make it obvious that the emission of light in particular can be achieved only by doing work. To emit electromagnetic waves, all you have to do is shake a charged particle, and this is clearly doing work, so that the emission is of energy.[p 22][note 10]
Einstein's 1905 demonstration of E = mc2
In his fourth of his 1905 Annus mirabilis papers,[p 21] Einstein presented a heuristic argument for the equivalence of mass and energy. Although, as discussed above, subsequent scholarship has established that his arguments fell short of a broadly definitive proof, the conclusions that he reached in this paper have stood the test of time.
Einstein took as starting assumptions his recently discovered formula for relativistic Doppler shift, the laws of conservation of energy and conservation of momentum, and the relationship between the frequency of light and its energy as implied by Maxwell's equations.
Fig. 6-1 (top). Consider a system of plane waves of light having frequency [math]\displaystyle{ f }[/math] traveling in direction [math]\displaystyle{ \phi }[/math] relative to the x-axis of reference frame S. The frequency (and hence energy) of the waves as measured in frame S′ that is moving along the x-axis at velocity [math]\displaystyle{ v }[/math] is given by the relativistic Doppler shift formula which Einstein had developed in his 1905 paper on special relativity:[p 1]
- [math]\displaystyle{ \frac{f'}{f} = \frac{1 - (v/c) \cos{\phi}}{\sqrt{1 - v^2/c^2}} }[/math]
Fig. 6-1 (bottom). Consider an arbitrary body that is stationary in reference frame S. Let this body emit a pair of equal-energy light-pulses in opposite directions at angle [math]\displaystyle{ \phi }[/math] with respect to the x-axis. Each pulse has energy [math]\displaystyle{ L/2 }[/math]. Because of conservation of momentum, the body remains stationary in S after emission of the two pulses. Let [math]\displaystyle{ E_0 }[/math] be the energy of the body before emission of the two pulses and [math]\displaystyle{ E_1 }[/math] after their emission.
Next, consider the same system observed from frame S′ that is moving along the x-axis at speed [math]\displaystyle{ v }[/math] relative to frame S. In this frame, light from the forwards and reverse pulses will be relativistically Doppler-shifted. Let [math]\displaystyle{ H_0 }[/math] be the energy of the body measured in reference frame S′ before emission of the two pulses and [math]\displaystyle{ H_1 }[/math] after their emission. We obtain the following relationships:[p 21]
- [math]\displaystyle{ \begin{align} E_0 &= E_1 + \tfrac{1}{2}L + \tfrac{1}{2}L = E_1 + L \\[5mu] H_0 &= H_1 + \tfrac12 L \frac{1 - (v/c) \cos{\phi}}{\sqrt{1 - v^2/c^2}} + \tfrac12 L \frac{1 + (v/c) \cos{\phi}}{\sqrt{1 - v^2/c^2}} = H_1 + \frac{L}{{\sqrt{1 - v^2/c^2}}} \end{align} }[/math]
From the above equations, we obtain the following:
[math]\displaystyle{ \quad\quad (H_0 - E_0) - (H_1 - E_1) = L \left( \frac{1}{\sqrt{1 - v^2/c^2}} - 1 \right) }[/math] |
|
( ) |
The two differences of form [math]\displaystyle{ H - E }[/math] seen in the above equation have a straightforward physical interpretation. Since [math]\displaystyle{ H }[/math] and [math]\displaystyle{ E }[/math] are the energies of the arbitrary body in the moving and stationary frames, [math]\displaystyle{ H_0 - E_0 }[/math] and [math]\displaystyle{ H_1 - E_1 }[/math] represents the kinetic energies of the bodies before and after the emission of light (except for an additive constant that fixes the zero point of energy and is conventionally set to zero). Hence,
[math]\displaystyle{ \quad\quad K_0 - K_1 = L \left( \frac{1}{\sqrt{1 - v^2/c^2}} - 1 \right) }[/math] |
|
( ) |
Taking a Taylor series expansion and neglecting higher order terms, he obtained
[math]\displaystyle{ \quad\quad K_0 - K_1 = \frac{1}{2} \frac{ L}{c^2} v^2 }[/math] |
|
( ) |
Comparing the above expression with the classical expression for kinetic energy, K.E. = 1/2mv2, Einstein then noted: "If a body gives off the energy L in the form of radiation, its mass diminishes by L/c2."
Rindler has observed that Einstein's heuristic argument suggested merely that energy contributes to mass. In 1905, Einstein's cautious expression of the mass–energy relationship allowed for the possibility that "dormant" mass might exist that would remain behind after all the energy of a body was removed. By 1907, however, Einstein was ready to assert that all inertial mass represented a reserve of energy. "To equate all mass with energy required an act of aesthetic faith, very characteristic of Einstein."[12]:81–84 Einstein's bold hypothesis has been amply confirmed in the years subsequent to his original proposal.
For a variety of reasons, Einstein's original derivation is currently seldom taught. Besides the vigorous debate that continues until this day as to the formal correctness of his original derivation, the recognition of special relativity as being what Einstein called a "principle theory" has led to a shift away from reliance on electromagnetic phenomena to purely dynamic methods of proof.[72]
Elastic collisions
Examination of the collision products generated by particle accelerators around the world provides scientists evidence of the structure of the subatomic world and the natural laws governing it. Analysis of the collision products, the sum of whose masses may vastly exceed the masses of the incident particles, requires special relativity.[73]
In Newtonian mechanics, analysis of collisions involves use of the conservation laws for mass, momentum and energy. In relativistic mechanics, mass is not independently conserved, because it has been subsumed into the total relativistic energy. We illustrate the differences that arise between the Newtonian and relativistic treatments of particle collisions by examining the simple case of two perfectly elastic colliding particles of equal mass. (Inelastic collisions are discussed in Spacetime. Radioactive decay may be considered a sort of time-reversed inelastic collision.[73])
Elastic scattering of charged elementary particles deviates from ideality due to the production of Bremsstrahlung radiation.[74][75]
Newtonian analysis
Fig. 6-2 provides a demonstration of the result, familiar to billiard players, that if a stationary ball is struck elastically by another one of the same mass (assuming no sidespin, or "English"), then after collision, the diverging paths of the two balls will subtend a right angle. (a) In the stationary frame, an incident sphere traveling at 2v strikes a stationary sphere. (b) In the center of momentum frame, the two spheres approach each other symmetrically at ±v. After elastic collision, the two spheres rebound from each other with equal and opposite velocities ±u. Energy conservation requires that |u| = |v|. (c) Reverting to the stationary frame, the rebound velocities are v ± u. The dot product (v + u) • (v − u) = v2 − u2 = 0, indicating that the vectors are orthogonal.[12]:26–27
Relativistic analysis
Consider the elastic collision scenario in Fig. 6-3 between a moving particle colliding with an equal mass stationary particle. Unlike the Newtonian case, the angle between the two particles after collision is less than 90°, is dependent on the angle of scattering, and becomes smaller and smaller as the velocity of the incident particle approaches the speed of light:
The relativistic momentum and total relativistic energy of a particle are given by
[math]\displaystyle{ \quad\quad \vec{p} = \gamma m \vec{v} \quad \text{and} \quad E = \gamma m c^2 }[/math] |
|
( ) |
Conservation of momentum dictates that the sum of the momenta of the incoming particle and the stationary particle (which initially has momentum = 0) equals the sum of the momenta of the emergent particles:
[math]\displaystyle{ \quad\quad \gamma_1 m \vec{v_1} + 0 = \gamma_2 m \vec{v_2} + \gamma_3 m \vec{v_3} }[/math] |
|
( ) |
Likewise, the sum of the total relativistic energies of the incoming particle and the stationary particle (which initially has total energy mc2) equals the sum of the total energies of the emergent particles:
[math]\displaystyle{ \quad\quad \gamma_1 m c^2 + m c^2 = \gamma_2 m c^2 + \gamma_3 m c^2 }[/math] |
|
( ) |
Breaking down (6-5) into its components, replacing [math]\displaystyle{ v }[/math] with the dimensionless [math]\displaystyle{ \beta }[/math], and factoring out common terms from (6-5) and (6-6) yields the following:[p 23]
[math]\displaystyle{ \quad\quad \beta_1 \gamma_1 = \beta_2 \gamma_2 \cos{\theta} + \beta_3 \gamma_3 \cos{\phi} }[/math] |
|
( ) |
[math]\displaystyle{ \quad\quad \beta_2 \gamma_2 \sin{\theta} = \beta_3 \gamma_3 \sin{\phi} }[/math] |
|
( ) |
[math]\displaystyle{ \quad\quad \gamma_1 + 1 = \gamma_2 + \gamma_3 }[/math] |
|
( ) |
From these we obtain the following relationships:[p 23]
[math]\displaystyle{ \quad\quad \beta_2 = \frac{\beta_1 \sin{\phi}}{ \{ \beta_1^2 \sin^2{\phi} + \sin^2(\phi + \theta )/\gamma_1^2 \}^{1/2} } }[/math] |
|
( ) |
[math]\displaystyle{ \quad\quad \beta_3 = \frac{\beta_1 \sin{\theta}}{ \{ \beta_1^2 \sin^2{\theta} + \sin^2(\phi + \theta )/\gamma_1^2 \}^{1/2} } }[/math] |
|
( ) |
[math]\displaystyle{ \quad\quad \cos{(\phi + \theta)} = \frac{ (\gamma_1 - 1) \sin{\theta} \cos{\theta} }{ \{ (\gamma_1 + 1)^2 \sin^2 \theta + 4 \cos^2 \theta \}^{1/2} } }[/math] |
|
( ) |
For the symmetrical case in which [math]\displaystyle{ \phi = \theta }[/math] and [math]\displaystyle{ \beta_2 = \beta_3, }[/math] (6-12) takes on the simpler form:[p 23]
[math]\displaystyle{ \quad\quad \cos{\theta} = \frac{\beta_1}{ \{ 2/\gamma_1 + 3 \beta_1^2 - 2 \}^{1/2} } }[/math] |
|
( ) |
How far can you travel from the Earth?
Since nothing can travel faster than light, one might conclude that a human can never travel farther from Earth than ~100 light years. You would easily think that a traveler would never be able to reach more than the few solar systems which exist within the limit of 100 light years from Earth. However, because of time dilation, a hypothetical spaceship can travel thousands of light years during a passenger's lifetime. If a spaceship could be built that accelerates at a constant 1g, it will, after one year, be travelling at almost the speed of light as seen from Earth. This is described by:
[math]\displaystyle{ v(t) = \frac{at}{\sqrt{1+ a^2t^2/c^2}} }[/math]
where v(t) is the velocity at a time t, a is the acceleration of the spaceship and t is the coordinate time as measured by people on Earth.[p 24] Therefore, after one year of accelerating at 9.81 m/s2, the spaceship will be travelling at v = 0.712c and 0.946c after three years, relative to Earth. After three years of this acceleration, with the spaceship achieving a velocity of 94.6% of the speed of light relative to Earth, time dilation will result in each second experienced on the spaceship corresponding to 3.1 seconds back on Earth. During their journey, people on Earth will experience more time than they do - since their clocks (all physical phenomena) would really be ticking 3.1 times faster than those of the spaceship. A 5-year round trip for the traveller will take 6.5 Earth years and cover a distance of over 6 light-years. A 20-year round trip for them (5 years accelerating, 5 decelerating, twice each) will land them back on Earth having travelled for 335 Earth years and a distance of 331 light years.[76] A full 40-year trip at 1g will appear on Earth to last 58,000 years and cover a distance of 55,000 light years. A 40-year trip at 1.1g will take 148,000 Earth years and cover about 140,000 light years. A one-way 28 year (14 years accelerating, 14 decelerating as measured with the astronaut's clock) trip at 1g acceleration could reach 2,000,000 light-years to the Andromeda Galaxy.[76] This same time dilation is why a muon travelling close to c is observed to travel much farther than c times its half-life (when at rest).[77]
Relativity and unifying electromagnetism
Theoretical investigation in classical electromagnetism led to the discovery of wave propagation. Equations generalizing the electromagnetic effects found that finite propagation speed of the E and B fields required certain behaviors on charged particles. The general study of moving charges forms the Liénard–Wiechert potential, which is a step towards special relativity.
The Lorentz transformation of the electric field of a moving charge into a non-moving observer's reference frame results in the appearance of a mathematical term commonly called the magnetic field. Conversely, the magnetic field generated by a moving charge disappears and becomes a purely electrostatic field in a comoving frame of reference. Maxwell's equations are thus simply an empirical fit to special relativistic effects in a classical model of the Universe. As electric and magnetic fields are reference frame dependent and thus intertwined, one speaks of electromagnetic fields. Special relativity provides the transformation rules for how an electromagnetic field in one inertial frame appears in another inertial frame.
Maxwell's equations in the 3D form are already consistent with the physical content of special relativity, although they are easier to manipulate in a manifestly covariant form, that is, in the language of tensor calculus.[78]
Theories of relativity and quantum mechanics
Special relativity can be combined with quantum mechanics to form relativistic quantum mechanics and quantum electrodynamics. How general relativity and quantum mechanics can be unified is one of the unsolved problems in physics; quantum gravity and a "theory of everything", which require a unification including general relativity too, are active and ongoing areas in theoretical research.
The early Bohr–Sommerfeld atomic model explained the fine structure of alkali metal atoms using both special relativity and the preliminary knowledge on quantum mechanics of the time.[79]
In 1928, Paul Dirac constructed an influential relativistic wave equation, now known as the Dirac equation in his honour,[p 25] that is fully compatible both with special relativity and with the final version of quantum theory existing after 1926. This equation not only described the intrinsic angular momentum of the electrons called spin, it also led to the prediction of the antiparticle of the electron (the positron),[p 25][p 26] and fine structure could only be fully explained with special relativity. It was the first foundation of relativistic quantum mechanics.
On the other hand, the existence of antiparticles leads to the conclusion that relativistic quantum mechanics is not enough for a more accurate and complete theory of particle interactions. Instead, a theory of particles interpreted as quantized fields, called quantum field theory, becomes necessary; in which particles can be created and destroyed throughout space and time.
Status
Special relativity in its Minkowski spacetime is accurate only when the absolute value of the gravitational potential is much less than c2 in the region of interest.[80] In a strong gravitational field, one must use general relativity. General relativity becomes special relativity at the limit of a weak field. At very small scales, such as at the Planck length and below, quantum effects must be taken into consideration resulting in quantum gravity. But at macroscopic scales and in the absence of strong gravitational fields, special relativity is experimentally tested to extremely high degree of accuracy (10−20)[81] and thus accepted by the physics community. Experimental results which appear to contradict it are not reproducible and are thus widely believed to be due to experimental errors.
Special relativity is mathematically self-consistent, and it is an organic part of all modern physical theories, most notably quantum field theory, string theory, and general relativity (in the limiting case of negligible gravitational fields).
Newtonian mechanics mathematically follows from special relativity at small velocities (compared to the speed of light) – thus Newtonian mechanics can be considered as a special relativity of slow moving bodies. See classical mechanics for a more detailed discussion.
Several experiments predating Einstein's 1905 paper are now interpreted as evidence for relativity. Of these it is known Einstein was aware of the Fizeau experiment before 1905,[82] and historians have concluded that Einstein was at least aware of the Michelson–Morley experiment as early as 1899 despite claims he made in his later years that it played no role in his development of the theory.[14]
- The Fizeau experiment (1851, repeated by Michelson and Morley in 1886) measured the speed of light in moving media, with results that are consistent with relativistic addition of colinear velocities.
- The famous Michelson–Morley experiment (1881, 1887) gave further support to the postulate that detecting an absolute reference velocity was not achievable. It should be stated here that, contrary to many alternative claims, it said little about the invariance of the speed of light with respect to the source and observer's velocity, as both source and observer were travelling together at the same velocity at all times.
- The Trouton–Noble experiment (1903) showed that the torque on a capacitor is independent of position and inertial reference frame.
- The Experiments of Rayleigh and Brace (1902, 1904) showed that length contraction does not lead to birefringence for a co-moving observer, in accordance with the relativity principle.
Particle accelerators routinely accelerate and measure the properties of particles moving at near the speed of light, where their behavior is completely consistent with relativity theory and inconsistent with the earlier Newtonian mechanics. These machines would simply not work if they were not engineered according to relativistic principles. In addition, a considerable number of modern experiments have been conducted to test special relativity. Some examples:
- Tests of relativistic energy and momentum – testing the limiting speed of particles
- Ives–Stilwell experiment – testing relativistic Doppler effect and time dilation
- Experimental testing of time dilation – relativistic effects on a fast-moving particle's half-life
- Kennedy–Thorndike experiment – time dilation in accordance with Lorentz transformations
- Hughes–Drever experiment – testing isotropy of space and mass
- Modern searches for Lorentz violation – various modern tests
- Experiments to test emission theory demonstrated that the speed of light is independent of the speed of the emitter.
- Experiments to test the aether drag hypothesis – no "aether flow obstruction".
Technical discussion of spacetime
Geometry of spacetime
Comparison between flat Euclidean space and Minkowski space
Special relativity uses a "flat" 4-dimensional Minkowski space – an example of a spacetime. Minkowski spacetime appears to be very similar to the standard 3-dimensional Euclidean space, but there is a crucial difference with respect to time.
In 3D space, the differential of distance (line element) ds is defined by
[math]\displaystyle{ ds^2 = d\mathbf{x} \cdot d\mathbf{x} = dx_1^2 + dx_2^2 + dx_3^2, }[/math]
where dx = (dx1, dx2, dx3) are the differentials of the three spatial dimensions. In Minkowski geometry, there is an extra dimension with coordinate X0 derived from time, such that the distance differential fulfills
[math]\displaystyle{ ds^2 = -dX_0^2 + dX_1^2 + dX_2^2 + dX_3^2, }[/math]
where dX = (dX0, dX1, dX2, dX3) are the differentials of the four spacetime dimensions. This suggests a deep theoretical insight: special relativity is simply a rotational symmetry of our spacetime, analogous to the rotational symmetry of Euclidean space (see Fig. 10-1).[84] Just as Euclidean space uses a Euclidean metric, so spacetime uses a Minkowski metric. Basically, special relativity can be stated as the invariance of any spacetime interval (that is the 4D distance between any two events) when viewed from any inertial reference frame. All equations and effects of special relativity can be derived from this rotational symmetry (the Poincaré group) of Minkowski spacetime.
The actual form of ds above depends on the metric and on the choices for the X0 coordinate. To make the time coordinate look like the space coordinates, it can be treated as imaginary: X0 = ict (this is called a Wick rotation). According to Misner, Thorne and Wheeler (1971, §2.3), ultimately the deeper understanding of both special and general relativity will come from the study of the Minkowski metric (described below) and to take X0 = ct, rather than a "disguised" Euclidean metric using ict as the time coordinate.
Some authors use X0 = t, with factors of c elsewhere to compensate; for instance, spatial coordinates are divided by c or factors of c±2 are included in the metric tensor.[85] These numerous conventions can be superseded by using natural units where c = 1. Then space and time have equivalent units, and no factors of c appear anywhere.
3D spacetime
If we reduce the spatial dimensions to 2, so that we can represent the physics in a 3D space
[math]\displaystyle{ ds^2 = dx_1^2 + dx_2^2 - c^2 dt^2, }[/math]
we see that the null geodesics lie along a dual-cone (see Fig. 10-2) defined by the equation;
[math]\displaystyle{ ds^2 = 0 = dx_1^2 + dx_2^2 - c^2 dt^2 }[/math]
or simply
[math]\displaystyle{ dx_1^2 + dx_2^2 = c^2 dt^2, }[/math]
which is the equation of a circle of radius c dt.
4D spacetime
If we extend this to three spatial dimensions, the null geodesics are the 4-dimensional cone:
[math]\displaystyle{ ds^2 = 0 = dx_1^2 + dx_2^2 + dx_3^2 - c^2 dt^2 }[/math]
so
[math]\displaystyle{ dx_1^2 + dx_2^2 + dx_3^2 = c^2 dt^2. }[/math]
As illustrated in Fig. 10-3, the null geodesics can be visualized as a set of continuous concentric spheres with radii = c dt.
This null dual-cone represents the "line of sight" of a point in space. That is, when we look at the stars and say "The light from that star which I am receiving is X years old", we are looking down this line of sight: a null geodesic. We are looking at an event a distance [math]\displaystyle{ d = \sqrt{x_1^2 + x_2^2 + x_3^2} }[/math] away and a time d/c in the past. For this reason the null dual cone is also known as the "light cone". (The point in the lower left of the Fig. 10-2 represents the star, the origin represents the observer, and the line represents the null geodesic "line of sight".)
The cone in the −t region is the information that the point is "receiving", while the cone in the +t section is the information that the point is "sending".
The geometry of Minkowski space can be depicted using Minkowski diagrams, which are useful also in understanding many of the thought experiments in special relativity.
Physics in spacetime
Transformations of physical quantities between reference frames
Above, the Lorentz transformation for the time coordinate and three space coordinates illustrates that they are intertwined. This is true more generally: certain pairs of "timelike" and "spacelike" quantities naturally combine on equal footing under the same Lorentz transformation.
The Lorentz transformation in standard configuration above, that is, for a boost in the x-direction, can be recast into matrix form as follows:
[math]\displaystyle{ \begin{pmatrix} ct'\\ x'\\ y'\\ z' \end{pmatrix} = \begin{pmatrix} \gamma & -\beta\gamma & 0 & 0\\ -\beta\gamma & \gamma & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} ct\\ x\\ y\\ z \end{pmatrix} = \begin{pmatrix} \gamma ct- \gamma\beta x\\ \gamma x - \beta \gamma ct \\ y\\ z \end{pmatrix}. }[/math]
In Newtonian mechanics, quantities that have magnitude and direction are mathematically described as 3d vectors in Euclidean space, and in general they are parametrized by time. In special relativity, this notion is extended by adding the appropriate timelike quantity to a spacelike vector quantity, and we have 4d vectors, or "four-vectors", in Minkowski spacetime. The components of vectors are written using tensor index notation, as this has numerous advantages. The notation makes it clear the equations are manifestly covariant under the Poincaré group, thus bypassing the tedious calculations to check this fact. In constructing such equations, we often find that equations previously thought to be unrelated are, in fact, closely connected being part of the same tensor equation. Recognizing other physical quantities as tensors simplifies their transformation laws. Throughout, upper indices (superscripts) are contravariant indices rather than exponents except when they indicate a square (this should be clear from the context), and lower indices (subscripts) are covariant indices. For simplicity and consistency with the earlier equations, Cartesian coordinates will be used.
The simplest example of a four-vector is the position of an event in spacetime, which constitutes a timelike component ct and spacelike component x = (x, y, z), in a contravariant position four-vector with components: [math]\displaystyle{ X^\nu = (X^0, X^1, X^2, X^3)= (ct, x, y, z) = (ct, \mathbf{x} ). }[/math] where we define X0 = ct so that the time coordinate has the same dimension of distance as the other spatial dimensions; so that space and time are treated equally.[86][87][88] Now the transformation of the contravariant components of the position 4-vector can be compactly written as:
[math]\displaystyle{ X^{\mu'}=\Lambda^{\mu'}{}_\nu X^\nu }[/math]
where there is an implied summation on [math]\displaystyle{ \nu }[/math] from 0 to 3, and [math]\displaystyle{ \Lambda^{\mu'}{}_{\nu} }[/math] is a matrix.
More generally, all contravariant components of a four-vector [math]\displaystyle{ T^\nu }[/math] transform from one frame to another frame by a Lorentz transformation: [math]\displaystyle{ T^{\mu'} = \Lambda^{\mu'}{}_{\nu} T^\nu }[/math]
Examples of other 4-vectors include the four-velocity [math]\displaystyle{ U^\mu, }[/math] defined as the derivative of the position 4-vector with respect to proper time: [math]\displaystyle{ U^\mu = \frac{dX^\mu}{d\tau} = \gamma(v)( c , v_x , v_y, v_z ) = \gamma(v) (c, \mathbf{v} ). }[/math] where the Lorentz factor is: [math]\displaystyle{ \gamma(v)= \frac{1}{\sqrt{1 - v^2/c^2 }} \qquad v^2 = v_x^2 + v_y^2 + v_z^2. }[/math]
The relativistic energy [math]\displaystyle{ E = \gamma(v)mc^2 }[/math] and relativistic momentum [math]\displaystyle{ \mathbf{p} = \gamma(v)m \mathbf{v} }[/math] of an object are respectively the timelike and spacelike components of a contravariant four-momentum vector:
[math]\displaystyle{ P^\mu = m U^\mu = m\gamma(v)(c,v_x,v_y,v_z)= \left (\frac{E}{c},p_x,p_y,p_z \right ) = \left (\frac{E}{c}, \mathbf{p} \right ). }[/math] where m is the invariant mass.
The four-acceleration is the proper time derivative of 4-velocity: [math]\displaystyle{ A^\mu = \frac{d U^\mu}{d\tau}. }[/math]
The transformation rules for three-dimensional velocities and accelerations are very awkward; even above in standard configuration the velocity equations are quite complicated owing to their non-linearity. On the other hand, the transformation of four-velocity and four-acceleration are simpler by means of the Lorentz transformation matrix.
The four-gradient of a scalar field φ transforms covariantly rather than contravariantly: [math]\displaystyle{ \begin{pmatrix} \dfrac{1}{c} \dfrac{\partial \phi}{\partial t'} & \dfrac{\partial \phi}{\partial x'} & \dfrac{\partial \phi}{\partial y'} & \dfrac{\partial \phi}{\partial z'} \end{pmatrix} = \begin{pmatrix} \dfrac{1}{c} \dfrac{\partial \phi}{\partial t} & \dfrac{\partial \phi}{\partial x} & \dfrac{\partial \phi}{\partial y} & \dfrac{\partial \phi}{\partial z} \end{pmatrix} \begin{pmatrix} \gamma & +\beta\gamma & 0 & 0\\ +\beta\gamma & \gamma & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}. }[/math]
which is the transpose of:
[math]\displaystyle{ (\partial_{\mu'} \phi) = \Lambda_{\mu'}{}^{\nu} (\partial_\nu \phi)\qquad \partial_{\mu} \equiv \frac{\partial}{\partial x^{\mu}}. }[/math]
only in Cartesian coordinates. It's the covariant derivative which transforms in manifest covariance, in Cartesian coordinates this happens to reduce to the partial derivatives, but not in other coordinates.
More generally, the covariant components of a 4-vector transform according to the inverse Lorentz transformation: [math]\displaystyle{ T_{\mu'} = \Lambda_{\mu'}{}^{\nu} T_\nu, }[/math] where [math]\displaystyle{ \Lambda_{\mu'}{}^{\nu} }[/math] is the reciprocal matrix of [math]\displaystyle{ \Lambda^{\mu'}{}_{\nu} }[/math].
The postulates of special relativity constrain the exact form the Lorentz transformation matrices take.
More generally, most physical quantities are best described as (components of) tensors. So to transform from one frame to another, we use the well-known tensor transformation law[89] [math]\displaystyle{ T^{\alpha' \beta' \cdots \zeta'}_{\theta' \iota' \cdots \kappa'} = \Lambda^{\alpha'}{}_{\mu} \Lambda^{\beta'}{}_{\nu} \cdots \Lambda^{\zeta'}{}_{\rho} \Lambda_{\theta'}{}^{\sigma} \Lambda_{\iota'}{}^{\upsilon} \cdots \Lambda_{\kappa'}{}^{\phi} T^{\mu \nu \cdots \rho}_{\sigma \upsilon \cdots \phi} }[/math] where [math]\displaystyle{ \Lambda_{\chi'}{}^{\psi} }[/math] is the reciprocal matrix of [math]\displaystyle{ \Lambda^{\chi'}{}_{\psi} }[/math]. All tensors transform by this rule.
An example of a four-dimensional second order antisymmetric tensor is the relativistic angular momentum, which has six components: three are the classical angular momentum, and the other three are related to the boost of the center of mass of the system. The derivative of the relativistic angular momentum with respect to proper time is the relativistic torque, also second order antisymmetric tensor.
The electromagnetic field tensor is another second order antisymmetric tensor field, with six components: three for the electric field and another three for the magnetic field. There is also the stress–energy tensor for the electromagnetic field, namely the electromagnetic stress–energy tensor.
Metric
The metric tensor allows one to define the inner product of two vectors, which in turn allows one to assign a magnitude to the vector. Given the four-dimensional nature of spacetime the Minkowski metric η has components (valid with suitably chosen coordinates) which can be arranged in a 4 × 4 matrix: [math]\displaystyle{ \eta_{\alpha\beta} = \begin{pmatrix} -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} }[/math] which is equal to its reciprocal, [math]\displaystyle{ \eta^{\alpha\beta} }[/math], in those frames. Throughout we use the signs as above, different authors use different conventions – see Minkowski metric alternative signs.
The Poincaré group is the most general group of transformations which preserves the Minkowski metric:
[math]\displaystyle{ \eta_{\alpha\beta} = \eta_{\mu'\nu'} \Lambda^{\mu'}{}_\alpha \Lambda^{\nu'}{}_\beta }[/math]
and this is the physical symmetry underlying special relativity.
The metric can be used for raising and lowering indices on vectors and tensors. Invariants can be constructed using the metric, the inner product of a 4-vector T with another 4-vector S is:
[math]\displaystyle{ T^{\alpha}S_{\alpha}=T^{\alpha}\eta_{\alpha\beta}S^{\beta} = T_{\alpha}\eta^{\alpha\beta}S_{\beta} = \text{invariant scalar} }[/math]
Invariant means that it takes the same value in all inertial frames, because it is a scalar (0 rank tensor), and so no Λ appears in its trivial transformation. The magnitude of the 4-vector T is the positive square root of the inner product with itself: [math]\displaystyle{ |\mathbf{T}| = \sqrt{T^{\alpha}T_{\alpha}} }[/math]
One can extend this idea to tensors of higher order, for a second order tensor we can form the invariants: [math]\displaystyle{ T^{\alpha}{}_{\alpha},T^{\alpha}{}_{\beta}T^{\beta}{}_{\alpha},T^{\alpha}{}_{\beta}T^{\beta}{}_{\gamma}T^{\gamma}{}_{\alpha} = \text{invariant scalars}, }[/math] similarly for higher order tensors. Invariant expressions, particularly inner products of 4-vectors with themselves, provide equations that are useful for calculations, because one does not need to perform Lorentz transformations to determine the invariants.
Relativistic kinematics and invariance
The coordinate differentials transform also contravariantly: [math]\displaystyle{ dX^{\mu'}=\Lambda^{\mu'}{}_\nu dX^\nu }[/math] so the squared length of the differential of the position four-vector dXμ constructed using [math]\displaystyle{ d\mathbf{X}^2 = dX^\mu \,dX_\mu = \eta_{\mu\nu}\,dX^\mu \,dX^\nu = -(c\,dt)^2+(dx)^2+(dy)^2+(dz)^2 }[/math] is an invariant. Notice that when the line element dX2 is negative that √−dX2 is the differential of proper time, while when dX2 is positive, √dX2 is differential of the proper distance.
The 4-velocity Uμ has an invariant form: [math]\displaystyle{ \mathbf U^2 = \eta_{\nu\mu} U^\nu U^\mu = -c^2 \,, }[/math] which means all velocity four-vectors have a magnitude of c. This is an expression of the fact that there is no such thing as being at coordinate rest in relativity: at the least, you are always moving forward through time. Differentiating the above equation by τ produces: [math]\displaystyle{ 2\eta_{\mu\nu}A^\mu U^\nu = 0. }[/math] So in special relativity, the acceleration four-vector and the velocity four-vector are orthogonal.
Relativistic dynamics and invariance
The invariant magnitude of the momentum 4-vector generates the energy–momentum relation: [math]\displaystyle{ \mathbf{P}^2 = \eta^{\mu\nu}P_\mu P_\nu = -\left (\frac{E}{c} \right )^2 + p^2 . }[/math]
We can work out what this invariant is by first arguing that, since it is a scalar, it does not matter in which reference frame we calculate it, and then by transforming to a frame where the total momentum is zero. [math]\displaystyle{ \mathbf{P}^2 = - \left (\frac{E_\text{rest}}{c} \right )^2 = - (m c)^2 . }[/math]
We see that the rest energy is an independent invariant. A rest energy can be calculated even for particles and systems in motion, by translating to a frame in which momentum is zero.
The rest energy is related to the mass according to the celebrated equation discussed above: [math]\displaystyle{ E_\text{rest} = m c^2. }[/math]
The mass of systems measured in their center of momentum frame (where total momentum is zero) is given by the total energy of the system in this frame. It may not be equal to the sum of individual system masses measured in other frames.
To use Newton's third law of motion, both forces must be defined as the rate of change of momentum with respect to the same time coordinate. That is, it requires the 3D force defined above. Unfortunately, there is no tensor in 4D which contains the components of the 3D force vector among its components.
If a particle is not traveling at c, one can transform the 3D force from the particle's co-moving reference frame into the observer's reference frame. This yields a 4-vector called the four-force. It is the rate of change of the above energy momentum four-vector with respect to proper time. The covariant version of the four-force is: [math]\displaystyle{ F_\nu = \frac{d P_{\nu}}{d \tau} = m A_\nu }[/math]
In the rest frame of the object, the time component of the four-force is zero unless the "invariant mass" of the object is changing (this requires a non-closed system in which energy/mass is being directly added or removed from the object) in which case it is the negative of that rate of change of mass, times c. In general, though, the components of the four-force are not equal to the components of the three-force, because the three force is defined by the rate of change of momentum with respect to coordinate time, that is, dp/dt while the four-force is defined by the rate of change of momentum with respect to proper time, that is, dp/dτ.
In a continuous medium, the 3D density of force combines with the density of power to form a covariant 4-vector. The spatial part is the result of dividing the force on a small cell (in 3-space) by the volume of that cell. The time component is −1/c times the power transferred to that cell divided by the volume of the cell. This will be used below in the section on electromagnetism.
See also
- People:
- Relativity:
- Physics:
- Mathematics:
- Philosophy:
- Paradoxes:
- Ehrenfest paradox
- Bell's spaceship paradox
- Velocity composition paradox
- Lighthouse paradox
Notes
- ↑ Einstein himself, in The Foundations of the General Theory of Relativity, Ann. Phys. 49 (1916), writes "The word 'special' is meant to intimate that the principle is restricted to the case ...". See p. 111 of The Principle of Relativity, A. Einstein, H. A. Lorentz, H. Weyl, H. Minkowski, Dover reprint of 1923 translation by Methuen and Company.]
- ↑ Wald, General Relativity, p. 60: "... the special theory of relativity asserts that spacetime is the manifold [math]\displaystyle{ \mathbb{R}^4 }[/math] with a flat metric of Lorentz signature defined on it. Conversely, the entire content of special relativity ... is contained in this statement ..."
- ↑ In a spacetime setting, the length of a moving rigid object is the spatial distance between the ends of the object measured at the same time. In the rest frame of the object the simultaneity is not required.
- ↑ The results of the Michelson–Morley experiment led George Francis FitzGerald and Hendrik Lorentz independently to propose the phenomenon of length contraction. Lorentz believed that length contraction represented a physical contraction of the atoms making up an object. He envisioned no fundamental change in the nature of space and time.[26]:62–68
Lorentz expected that length contraction would result in compressive strains in an object that should result in measurable effects. Such effects would include optical effects in transparent media, such as optical rotation[p 11] and induction of double refraction,[p 12] and the induction of torques on charged condensers moving at an angle with respect to the aether.[p 12] Lorentz was perplexed by experiments such as the Trouton–Noble experiment and the experiments of Rayleigh and Brace which failed to validate his theoretical expectations.[26] - ↑ For mathematical consistency, Lorentz proposed a new time variable, the "local time", called that because it depended on the position of a moving body, following the relation [math]\displaystyle{ t' = t - vx/c^2 }[/math].[p 13] Lorentz considered local time not to be "real"; rather, it represented an ad hoc change of variable.[27]:51,80
Impressed by Lorentz's "most ingenious idea", Poincaré saw more in local time than a mere mathematical trick. It represented the actual time that would be shown on a moving observer's clocks. On the other hand, Poincaré did not consider this measured time to be the "true time" that would be exhibited by clocks at rest in the aether. Poincaré made no attempt to redefine the concepts of space and time. To Poincaré, Lorentz transformation described the apparent states of the field for a moving observer. True states remained those defined with respect to the ether.[28] - ↑ This concept is counterintuitive at least for the fact that, in contrast to usual concepts of distance, it may assume negative values (is not positive definite for non-coinciding events), and that the square-denotation is misleading. This negative square lead to, now not broadly used, concepts of imaginary time. It is immediate that the negative of [math]\displaystyle{ \Delta s^2 }[/math] is also an invariant, generated by a variant of the metric signature of spacetime.
- ↑ The invariance of Δs2 under standard Lorentz transformation in analogous to the invariance of squared distances Δr2 under rotations in Euclidean space. Although space and time have an equal footing in relativity, the minus sign in front of the spatial terms marks space and time as being of essentially different character. They are not the same. Because it treats time differently than it treats the 3 spatial dimensions, Minkowski space differs from four-dimensional Euclidean space.
- ↑ The refractive index dependence of the presumed partial aether-drag was eventually confirmed by Pieter Zeeman in 1914–1915, long after special relativity had been accepted by the mainstream. Using a scaled-up version of Michelson's apparatus connected directly to Amsterdam's main water conduit, Zeeman was able to perform extended measurements using monochromatic light ranging from violet (4358 Å) through red (6870 Å).[p 17][p 18]
- ↑ Even though it has been many decades since Terrell and Penrose published their observations, popular writings continue to conflate measurement versus appearance. For example, Michio Kaku wrote in Einstein's Cosmos (W. W. Norton & Company, 2004. p. 65): "... imagine that the speed of light is only 20 miles per hour. If a car were to go down the street, it might look compressed in the direction of motion, being squeezed like an accordion down to perhaps 1 inch in length."
- ↑ In a letter to Carl Seelig in 1955, Einstein wrote "I had already previously found that Maxwell's theory did not account for the micro-structure of radiation and could therefore have no general validity.", Einstein letter to Carl Seelig, 1955.
Primary sources
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Albert Einstein (1905) "Zur Elektrodynamik bewegter Körper", Annalen der Physik 17: 891; English translation On the Electrodynamics of Moving Bodies by George Barker Jeffery and Wilfrid Perrett (1923); Another English translation On the Electrodynamics of Moving Bodies by Megh Nad Saha (1920).
- ↑ "Science and Common Sense", P. W. Bridgman, The Scientific Monthly, Vol. 79, No. 1 (Jul. 1954), pp. 32–39.
- ↑ The Electromagnetic Mass and Momentum of a Spinning Electron, G. Breit, Proceedings of the National Academy of Sciences, Vol. 12, p.451, 1926
- ↑ Kinematics of an electron with an axis. Phil. Mag. 3:1-22. L. H. Thomas.]
- ↑ 5.0 5.1 Einstein, Autobiographical Notes, 1949.
- ↑ Einstein, "Fundamental Ideas and Methods of the Theory of Relativity", 1920
- ↑ Einstein, On the Relativity Principle and the Conclusions Drawn from It, 1907; "The Principle of Relativity and Its Consequences in Modern Physics", 1910; "The Theory of Relativity", 1911; Manuscript on the Special Theory of Relativity, 1912; Theory of Relativity, 1913; Einstein, Relativity, the Special and General Theory, 1916; The Principal Ideas of the Theory of Relativity, 1916; What Is The Theory of Relativity?, 1919; The Principle of Relativity (Princeton Lectures), 1921; Physics and Reality, 1936; The Theory of Relativity, 1949.
- ↑ Yaakov Friedman (2004). Physical Applications of Homogeneous Balls. Progress in Mathematical Physics. 40. pp. 1–21. ISBN 978-0-8176-3339-4.
- ↑ Das, A. (1993) The Special Theory of Relativity, A Mathematical Exposition, Springer, ISBN 0-387-94042-1.
- ↑ Schutz, J. (1997) Independent Axioms for Minkowski Spacetime, Addison Wesley Longman Limited, ISBN 0-582-31760-6.
- ↑ Lorentz, H.A. (1902). "The rotation of the plane of polarization in moving media". Huygens Institute - Royal Netherlands Academy of Arts and Sciences (KNAW) 4: 669–678. Bibcode: 1901KNAB....4..669L. http://www.dwc.knaw.nl/DL/publications/PU00014324.pdf. Retrieved 15 November 2018.
- ↑ 12.0 12.1 Lorentz, H. A. (1904). "Electromagnetic phenomena in a system moving with any velocity smaller than that of light". Huygens Institute - Royal Netherlands Academy of Arts and Sciences (KNAW) 6: 809–831. Bibcode: 1903KNAB....6..809L. http://www.dwc.knaw.nl/DL/publications/PU00014148.pdf. Retrieved 15 November 2018.
- ↑ Lorentz, Hendrik (1895). "Investigation of oscillations excited by oscillating ions". Attempt at a Theory of Electrical and Optical Phenomena in Moving Bodies (Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern). Leiden: E. J. Brill. (subsection § 31). https://en.wikisource.org/wiki/Translation:Attempt_of_a_Theory_of_Electrical_and_Optical_Phenomena_in_Moving_Bodies/Section_III.
- ↑ Lin, Shih-Chun; Giallorenzi, Thomas G. (1979). "Sensitivity analysis of the Sagnac-effect optical-fiber ring interferometer". Applied Optics 18 (6): 915–931. doi:10.1364/AO.18.000915. PMID 20208844. Bibcode: 1979ApOpt..18..915L.
- ↑ Shaw, R. (1962). "Length Contraction Paradox". American Journal of Physics 30 (1): 72. doi:10.1119/1.1941907. Bibcode: 1962AmJPh..30...72S.
- ↑ G. A. Benford; D. L. Book; W. A. Newcomb (1970). "The Tachyonic Antitelephone". Physical Review D 2 (2): 263–265. doi:10.1103/PhysRevD.2.263. Bibcode: 1970PhRvD...2..263B.
- ↑ Zeeman, Pieter (1914). "Fresnel's coefficient for light of different colours. (First part)". Proc. Kon. Acad. Van Weten. 17: 445–451. Bibcode: 1914KNAB...17..445Z. https://archive.org/details/p1proceedingsofs17akad.
- ↑ Zeeman, Pieter (1915). "Fresnel's coefficient for light of different colours. (Second part)". Proc. Kon. Acad. Van Weten. 18: 398–408. Bibcode: 1915KNAB...18..398Z. https://archive.org/details/proceedingsofsec181koni.
- ↑ Terrell, James (15 November 1959). "Invisibility of the Lorentz Contraction". Physical Review 116 (4): 1041–1045. doi:10.1103/PhysRev.116.1041. Bibcode: 1959PhRv..116.1041T.
- ↑ Penrose, Roger (24 October 2008). "The Apparent Shape of a Relativistically Moving Sphere". Mathematical Proceedings of the Cambridge Philosophical Society 55 (1): 137–139. doi:10.1017/S0305004100033776. Bibcode: 1959PCPS...55..137P.
- ↑ 21.0 21.1 21.2 Does the inertia of a body depend upon its energy content? A. Einstein, Annalen der Physik. 18:639, 1905 (English translation by W. Perrett and G.B. Jeffery)
- ↑ On the Inertia of Energy Required by the Relativity Principle, A. Einstein, Annalen der Physik 23 (1907): 371–384
- ↑ 23.0 23.1 23.2 Champion, Frank Clive (1932). "On some close collisions of fast β-particles with electrons, photographed by the expansion method.". Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character (The Royal Society Publishing) 136 (830): 630–637. doi:10.1098/rspa.1932.0108. Bibcode: 1932RSPSA.136..630C.
- ↑ Baglio, Julien (26 May 2007). "Acceleration in special relativity: What is the meaning of "uniformly accelerated movement" ?". Physics Department, ENS Cachan. http://www.normalesup.org/~baglio/physique/acceleration.pdf.
- ↑ 25.0 25.1 P.A.M. Dirac (1930). "A Theory of Electrons and Protons". Proceedings of the Royal Society A126 (801): 360–365. doi:10.1098/rspa.1930.0013. Bibcode: 1930RSPSA.126..360D.
- ↑ C.D. Anderson (1933). "The Positive Electron". Phys. Rev. 43 (6): 491–494. doi:10.1103/PhysRev.43.491. Bibcode: 1933PhRv...43..491A.
References
- ↑ 1.0 1.1 1.2 Griffiths, David J. (2013). "Electrodynamics and Relativity". Introduction to Electrodynamics (4th ed.). Pearson. Chapter 12. ISBN 978-0-321-85656-2.
- ↑ 2.0 2.1 2.2 Jackson, John D. (1999). "Special Theory of Relativity". Classical Electrodynamics (3rd ed.). John Wiley & Sons, Inc.. Chapter 11. ISBN 0-471-30932-X.
- ↑ Goldstein, Herbert (1980). "Chapter 7: Special Relativity in Classical Mechanics". Classical Mechanics (2nd ed.). Addison-Wesley Publishing Company. ISBN 0-201-02918-9.
- ↑ 4.0 4.1 Lanczos, Cornelius (1970). "Chapter IX: Relativistic Mechanics". The Variational Principles of Mechanics (4th ed.). Dover Publications. ISBN 978-0-486-65067-8.
- ↑ "What is the experimental basis of Special Relativity?". Usenet Physics FAQ. October 2007. http://www.edu-observatory.org/physics-faq/Relativity/SR/experiments.html.
- ↑ Albert Einstein (2001). Relativity: The Special and the General Theory (Reprint of 1920 translation by Robert W. Lawson ed.). Routledge. p. 48. ISBN 978-0-415-25384-0. https://books.google.com/books?id=idb7wJiB6SsC&pg=PA50.
- ↑ The Feynman Lectures on Physics Vol. I Ch. 15-9: Equivalence of mass and energy
- ↑ Sean Carroll, Lecture Notes on General Relativity, ch. 1, "Special relativity and flat spacetime," http://ned.ipac.caltech.edu/level5/March01/Carroll3/Carroll1.html
- ↑ Koks, Don (2006). Explorations in Mathematical Physics: The Concepts Behind an Elegant Language (illustrated ed.). Springer Science & Business Media. p. 234. ISBN 978-0-387-32793-8. https://books.google.com/books?id=ObMb7l9-9loC. Extract of page 234
- ↑ Steane, Andrew M. (2012). Relativity Made Relatively Easy (illustrated ed.). OUP Oxford. p. 226. ISBN 978-0-19-966286-9. https://books.google.com/books?id=75rCErZkh7EC. Extract of page 226
- ↑ Edwin F. Taylor; John Archibald Wheeler (1992). Spacetime Physics: Introduction to Special Relativity. W. H. Freeman. ISBN 978-0-7167-2327-1. https://archive.org/details/spacetimephysics00edwi_0.
- ↑ 12.0 12.1 12.2 12.3 12.4 Rindler, Wolfgang (1977). Essential Relativity: Special, General, and Cosmological (illustrated ed.). Springer Science & Business Media. p. §1,11 p. 7. ISBN 978-3-540-07970-5. https://books.google.com/books?id=0J_dwCmQThgC&pg=PT148.
- ↑ Michael Polanyi (1974) Personal Knowledge: Towards a Post-Critical Philosophy, ISBN 0-226-67288-3, footnote page 10–11: Einstein reports, via Dr N Balzas in response to Polanyi's query, that "The Michelson–Morley experiment had no role in the foundation of the theory." and "..the theory of relativity was not founded to explain its outcome at all." [1]
- ↑ 14.0 14.1 Jeroen van Dongen (2009). "On the role of the Michelson–Morley experiment: Einstein in Chicago". Archive for History of Exact Sciences 63 (6): 655–663. doi:10.1007/s00407-009-0050-5. Bibcode: 2009arXiv0908.1545V.
- ↑ For a survey of such derivations, see Lucas and Hodgson, Spacetime and Electromagnetism, 1990
- ↑ Einstein, A., Lorentz, H. A., Minkowski, H., & Weyl, H. (1952). The Principle of Relativity: a collection of original memoirs on the special and general theory of relativity. Courier Dover Publications. p. 111. ISBN 978-0-486-60081-9. https://books.google.com/books?id=yECokhzsJYIC&pg=PA111.
- ↑ Collier, Peter (2017). A Most Incomprehensible Thing: Notes Towards a Very Gentle Introduction to the Mathematics of Relativity (3rd ed.). Incomprehensible Books. ISBN 9780957389465.
- ↑ Staley, Richard (2009), "Albert Michelson, the Velocity of Light, and the Ether Drift", Einstein's generation. The origins of the relativity revolution, Chicago: University of Chicago Press, ISBN 0-226-77057-5
- ↑ 19.0 19.1 19.2 19.3 19.4 19.5 19.6 19.7 David Morin (2007) Introduction to Classical Mechanics, Cambridge University Press, Cambridge, chapter 11, Appendix I, ISBN 1-139-46837-5.
- ↑ Miller, D. J. (2010). "A constructive approach to the special theory of relativity". American Journal of Physics 78 (6): 633–638. doi:10.1119/1.3298908. Bibcode: 2010AmJPh..78..633M.
- ↑ Taylor, Edwin; Wheeler, John Archibald (1992). Spacetime Physics (2nd ed.). W.H. Freeman & Co.. ISBN 978-0-7167-2327-1. https://archive.org/details/spacetimephysics00edwi_0.
- ↑ Callahan, James J. (2011). The Geometry of Spacetime: An Introduction to Special and General Relativity. New York: Springer. ISBN 9781441931429.
- ↑ P. G. Bergmann (1976) Introduction to the Theory of Relativity, Dover edition, Chapter IV, page 36 ISBN 0-486-63282-2.
- ↑ Mermin, N. David (1968). Space and Time in Special Relativity. McGraw-Hill. ISBN 978-0881334203. https://archive.org/details/spacetimeinspeci0000merm.
- ↑ Robert Resnick (1968). Introduction to special relativity. Wiley. pp. 62–63. ISBN 9780471717249. https://books.google.com/books?id=fsIRAQAAIAAJ.
- ↑ 26.0 26.1 Miller, Arthur I. (1998). Albert Einstein's Special Theory of Relativity: Emergence (1905) and Early Interpretation (1905–1911). Mew York: Springer-Verlag. ISBN 978-0-387-94870-6.
- ↑ Bernstein, Jeremy (2006). Secrets of the Old One: Einstein, 1905. Copernicus Books (imprint of Springer Science + Business Media). ISBN 978-0387-26005-1.
- ↑ Darrigol, Olivier (2005). "The Genesis of the Theory of Relativity". Séminaire Poincaré 1: 1–22. Bibcode: 2006eins.book....1D. http://www.bourbaphy.fr/darrigol2.pdf. Retrieved 15 November 2018.
- ↑ 29.0 29.1 29.2 Rindler, Wolfgang (1977). Essential Relativity (2nd ed.). New York: Springer-Verlag. ISBN 978-0-387-10090-6.
- ↑ 30.0 30.1 30.2 30.3 Taylor, Edwin F.; Wheeler, John Archibald (1966). Spacetime Physics (1st ed.). San Francisco: W. H. Freeman and Company. https://archive.org/details/spacetimephysics0000tayl.
- ↑ Ashby, Neil (2003). "Relativity in the Global Positioning System". Living Reviews in Relativity 6 (1): 1. doi:10.12942/lrr-2003-1. PMID 28163638. Bibcode: 2003LRR.....6....1A.
- ↑ Daniel Kleppner; David Kolenkow (1973). An Introduction to Mechanics. McGraw-Hill. pp. 468–70. ISBN 978-0-07-035048-9. https://archive.org/details/introductiontome00dani/page/468.
- ↑ 33.0 33.1 33.2 French, A. P. (1968). Special Relativity. New York: W. W. Norton & Company. ISBN 0-393-09793-5.
- ↑ Lewis, Gilbert Newton; Tolman, Richard Chase (1909). "The Principle of Relativity, and Non-Newtonian Mechanics". Proceedings of the American Academy of Arts and Sciences 44 (25): 709–726. doi:10.2307/20022495. https://en.wikisource.org/wiki/The_Principle_of_Relativity,_and_Non-Newtonian_Mechanics. Retrieved 22 August 2023.
- ↑ 35.0 35.1 Cuvaj, Camillo (1971). "Paul Langeyin and the Theory of Relativity". Japanese Studies in the History of Science 10: 113–142. http://www.isc.meiji.ac.jp/~sano/hssj/pdf/Cuvaj_C-1972-Langevin_Relativity-JSHS-No_10-pp113-142.pdf. Retrieved 12 June 2023.
- ↑ Cassidy, David C.; Holton, Gerald James; Rutherford, Floyd James (2002). Understanding Physics. Springer-Verlag. pp. 422. ISBN 978-0-387-98756-9. https://books.google.com/books?id=rpQo7f9F1xUC&pg=PA422.
- ↑ Cutner, Mark Leslie (2003). Astronomy, A Physical Perspective. Cambridge University Press. p. 128. ISBN 978-0-521-82196-4. https://books.google.com/books?id=2QVmiMW0O0MC&pg=PA128.
- ↑ Ellis, George F. R.; Williams, Ruth M. (2000). Flat and Curved Space-times (2n ed.). Oxford University Press. pp. 28–29. ISBN 978-0-19-850657-7. https://books.google.com/books?id=Hos31wty5WIC&pg=PA28.
- ↑ Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (2011). The feynman lectures on physics; vol I: The new millennium edition. Basic Books. p. 15-5. ISBN 978-0-465-02414-8. https://www.feynmanlectures.caltech.edu/I_15.html. Retrieved 12 June 2023.
- ↑ 40.0 40.1 Halliday, David; Resnick, Robert (1988). Fundamental Physics: Extended Third Edition. New York: John Wiley & sons. pp. 958–959. ISBN 0-471-81995-6.
- ↑ Adams, Steve (1997). Relativity: An introduction to space-time physics. CRC Press. p. 54. ISBN 978-0-7484-0621-0. https://books.google.com/books?id=1RV0AysEN4oC&pg=PA54.
- ↑ Langevin, Paul (1911). "L'Évolution de l'espace et du temps". Scientia 10: 31–54. https://en.wikisource.org/wiki/Translation:The_Evolution_of_Space_and_Time. Retrieved 20 June 2023.
- ↑ Debs, Talal A.; Redhead, Michael L.G. (1996). "The twin "paradox" and the conventionality of simultaneity". American Journal of Physics 64 (4): 384–392. doi:10.1119/1.18252. Bibcode: 1996AmJPh..64..384D.
- ↑ Tolman, Richard C. (1917). The Theory of the Relativity of Motion. Berkeley: University of California Press. p. 54. https://books.google.com/books?id=8yodAAAAMAAJ&q=54.
- ↑ Takeuchi, Tatsu. "Special Relativity Lecture Notes – Section 10". Virginia Tech. https://www1.phys.vt.edu/~takeuchi/relativity/notes/section10.html.
- ↑ Morin, David (2017). Special Relativity for the Enthusiastic Beginner. CreateSpace Independent Publishing Platform. pp. 90–92. ISBN 9781542323512.
- ↑ Gibbs, Philip. "Is Faster-Than-Light Travel or Communication Possible?". Department of Mathematics, University of California, Riverside. http://math.ucr.edu/home/baez/physics/Relativity/SpeedOfLight/FTL.html.
- ↑ Ginsburg, David (1989). Applications of Electrodynamics in Theoretical Physics and Astrophysics (illustrated ed.). CRC Press. p. 206. ISBN 978-2-88124-719-4. Bibcode: 1989aetp.book.....G. https://books.google.com/books?id=Lh0tjaBNzg0C. Extract of page 206
- ↑ Wesley C. Salmon (2006). Four Decades of Scientific Explanation. University of Pittsburgh. p. 107. ISBN 978-0-8229-5926-7. https://books.google.com/books?id=FHqOXCd06e8C., Section 3.7 page 107
- ↑ Lauginie, P. (2004). "Measuring Speed of Light: Why? Speed of what?". Proceedings of the Fifth International Conference for History of Science in Science Education. http://sci-ed.org/documents/Lauginie-M.pdf. Retrieved 3 July 2015.
- ↑ Stachel, J. (2005). "Fresnel's (dragging) coefficient as a challenge to 19th century optics of moving bodies". in Kox, A.J.. The universe of general relativity. Boston: Birkhäuser. pp. 1–13. ISBN 978-0-8176-4380-5. https://books.google.com/books?id=-KlBhDwUKF8C&pg=PA1. Retrieved 17 April 2012.
- ↑ Richard A. Mould (2001). Basic Relativity (2nd ed.). Springer. p. 8. ISBN 978-0-387-95210-9. https://books.google.com/books?id=lfGE-wyJYIUC&pg=PA8.
- ↑ Seidelmann, P. Kenneth, ed (1992). Explanatory Supplement to the Astronomical Almanac. ill Valley, Calif.: University Science Books. p. 393. ISBN 978-0-935702-68-2. https://archive.org/details/131123ExplanatorySupplementAstronomicalAlmanac/page/n209.
- ↑ Ferraro, Rafael; Sforza, Daniel M. (2005). "European Physical Society logo Arago (1810): the first experimental result against the ether". European Journal of Physics 26 (1): 195–204. doi:10.1088/0143-0807/26/1/020. Bibcode: 2005EJPh...26..195F.
- ↑ Dolan, Graham. "Airy's Water Telescope (1870)". The Royal Observatory Greenwich. http://www.royalobservatorygreenwich.org/articles.php?article=1069.
- ↑ Hollis, H. P. (1937). "Airy's water telescope". The Observatory 60: 103–107. Bibcode: 1937Obs....60..103H. http://adsbit.harvard.edu//full/1937Obs....60..103H/0000105.000.html. Retrieved 20 November 2018.
- ↑ Janssen, Michel; Stachel, John (2004). "The Optics and Electrodynamics of Moving Bodies". in Stachel, John. Going Critical. Springer. ISBN 978-1-4020-1308-9. https://www.mpiwg-berlin.mpg.de/Preprints/P265.PDF.
- ↑ Sher, D. (1968). "The Relativistic Doppler Effect". Journal of the Royal Astronomical Society of Canada 62: 105–111. Bibcode: 1968JRASC..62..105S. http://adsbit.harvard.edu//full/1968JRASC..62..105S/0000105.000.html. Retrieved 11 October 2018.
- ↑ Gill, T. P. (1965). The Doppler Effect. London: Logos Press Limited. pp. 6–9.
- ↑ Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (February 1977). "Relativistic Effects in Radiation". The Feynman Lectures on Physics: Volume 1. Reading, Massachusetts: Addison-Wesley. pp. 34–7 f. ISBN 9780201021165. https://feynmanlectures.caltech.edu/I_34.html.
- ↑ Cook, Helen. "Relativistic Distortion". Mathematics Department, University of British Columbia. http://www.math.ubc.ca/~cass/courses/m309-01a/cook/.
- ↑ Signell, Peter. "Appearances at Relativistic Speeds". Michigan State University, East Lansing, MI. https://stuff.mit.edu/afs/athena/course/8/8.20/www/m44.pdf.
- ↑ Kraus, Ute. "The Ball is Round". Institut für Physik Universität Hildesheim. http://www.spacetimetravel.org/fussball/fussball.html.
- ↑ Boas, Mary L. (1961). "Apparent Shape of Large Objects at Relativistic Speeds". American Journal of Physics 29 (5): 283. doi:10.1119/1.1937751. Bibcode: 1961AmJPh..29..283B.
- ↑ Müller, Thomas; Boblest, Sebastian (2014). "Visual appearance of wireframe objects in special relativity". European Journal of Physics 35 (6): 065025. doi:10.1088/0143-0807/35/6/065025. Bibcode: 2014EJPh...35f5025M.
- ↑ Zensus, J. Anton; Pearson, Timothy J. (1987). Superluminal Radio Sources (1st ed.). Cambridge, New York: Cambridge University Press. p. 3. ISBN 9780521345606.
- ↑ Chase, Scott I.. "Apparent Superluminal Velocity of Galaxies". Department of Mathematics, University of California, Riverside. http://math.ucr.edu/home/baez/physics/Relativity/SpeedOfLight/Superluminal/superluminal.html.
- ↑ Richmond, Michael. ""Superluminal" motions in astronomical sources". School of Physics and Astronomy, Rochester Institute of Technology. http://spiff.rit.edu/classes/phys200/lectures/superlum/superlum.html.
- ↑ Keel, Bill. "Jets, Superluminal Motion, and Gamma-Ray Bursts". Department of Physics and Astronomy, University of Alabama. http://pages.astronomy.ua.edu/keel/galaxies/jets.html.
- ↑ Max Jammer (1997). Concepts of Mass in Classical and Modern Physics. Courier Dover Publications. pp. 177–178. ISBN 978-0-486-29998-3. https://books.google.com/books?id=lYvz0_8aGsMC&pg=PA177.
- ↑ John J. Stachel (2002). Einstein from B to Z. Springer. p. 221. ISBN 978-0-8176-4143-6. https://books.google.com/books?id=OAsQ_hFjhrAC&pg=PA215.
- ↑ Fernflores, Francisco (2018). Einstein's Mass-Energy Equation, Volume I: Early History and Philosophical Foundations. New York: Momentum Pres. ISBN 978-1-60650-857-2.
- ↑ 73.0 73.1 Idema, Timon (17 April 2019). "Mechanics and Relativity. Chapter 14: Relativistic Collisions". California State University Affordable Learning Solutions Program. https://phys.libretexts.org/Bookshelves/University_Physics/Book:_Mechanics_and_Relativity_(Idema)/14:_Relativistic_Collisions.
- ↑ Nakel, Werner (1994). "The elementary process of bremsstrahlung". Physics Reports 243 (6): 317–353. doi:10.1016/0370-1573(94)00068-9. Bibcode: 1994PhR...243..317N.
- ↑ Halbert, M.L. (1972). "Review of Experiments on Nucleon-Nucleon Bremsstrahlung". in Austin, S.M.; Crawley, G.M.. The Two-Body Force in Nuclei. Boston, MA.: Springer.
- ↑ 76.0 76.1 "The Relativistic Rocket". http://math.ucr.edu/home/baez/physics/Relativity/SR/Rocket/rocket.html.
- ↑ The special theory of relativity shows that time and space are affected by motion . Library.thinkquest.org. Retrieved on 2013-04-24.
- ↑ E. J. Post (1962). Formal Structure of Electromagnetics: General Covariance and Electromagnetics. Dover Publications Inc.. ISBN 978-0-486-65427-0.
- ↑ R. Resnick; R. Eisberg (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd ed.). John Wiley & Sons. pp. 114–116. ISBN 978-0-471-87373-0. https://archive.org/details/quantumphysicsof00eisb/page/114.
- ↑ Øyvind Grøn; Sigbjørn Hervik (2007). Einstein's general theory of relativity: with modern applications in cosmology. Springer. p. 195. ISBN 978-0-387-69199-2. https://books.google.com/books?id=IyJhCHAryuUC. Extract of page 195 (with units where c=1)
- ↑ The number of works is vast, see as example:
Sidney Coleman; Sheldon L. Glashow (1997). "Cosmic Ray and Neutrino Tests of Special Relativity". Physics Letters B 405 (3–4): 249–252. doi:10.1016/S0370-2693(97)00638-2. Bibcode: 1997PhLB..405..249C.
An overview can be found on this page - ↑ John D. Norton, John D. (2004). "Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905". Archive for History of Exact Sciences 59 (1): 45–105. doi:10.1007/s00407-004-0085-6. Bibcode: 2004AHES...59...45N. http://philsci-archive.pitt.edu/archive/00001743/.
- ↑ J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. p. 58. ISBN 978-0-7167-0344-0.
- ↑ J.R. Forshaw; A.G. Smith (2009). Dynamics and Relativity. Wiley. p. 247. ISBN 978-0-470-01460-8.
- ↑ R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
- ↑ Jean-Bernard Zuber & Claude Itzykson, Quantum Field Theory, pg 5, ISBN 0-07-032071-3
- ↑ Charles W. Misner, Kip S. Thorne & John A. Wheeler, Gravitation, pg 51, ISBN 0-7167-0344-0
- ↑ George Sterman, An Introduction to Quantum Field Theory, pg 4, ISBN 0-521-31132-2
- ↑ Sean M. Carroll (2004). Spacetime and Geometry: An Introduction to General Relativity. Addison Wesley. p. 22. ISBN 978-0-8053-8732-2. https://books.google.com/books?id=1SKFQgAACAAJ.
Further reading
Texts by Einstein and text about history of special relativity
- Einstein, Albert (1920). Relativity: The Special and General Theory.
- Einstein, Albert (1996). The Meaning of Relativity. Fine Communications. ISBN 1-56731-136-9
- Logunov, Anatoly A. (2005). Henri Poincaré and the Relativity Theory (transl. from Russian by G. Pontocorvo and V. O. Soloviev, edited by V. A. Petrov). Nauka, Moscow.
Textbooks
- Charles Misner, Kip Thorne, and John Archibald Wheeler (1971) Gravitation. W. H. Freeman & Co. ISBN 0-7167-0334-3
- Post, E.J., 1997 (1962) Formal Structure of Electromagnetics: General Covariance and Electromagnetics. Dover Publications.
- Wolfgang Rindler (1991). Introduction to Special Relativity (2nd ed.), Oxford University Press. ISBN 978-0-19-853952-0; ISBN 0-19-853952-5
- Harvey R. Brown (2005). Physical relativity: space–time structure from a dynamical perspective, Oxford University Press, ISBN 0-19-927583-1; ISBN 978-0-19-927583-0
- Qadir, Asghar (1989). Relativity: An Introduction to the Special Theory. Singapore: World Scientific Publications. p. 128. ISBN 978-9971-5-0612-4. Bibcode: 1989rist.book.....Q. https://books.google.com/books?id=X5YofYrqFoAC.
- French, A. P. (1968). Special Relativity (M.I.T. Introductory Physics) (1st ed.). W. W. Norton & Company. ISBN 978-0393097931.
- Silberstein, Ludwik (1914). The Theory of Relativity.
- Lawrence Sklar (1977). Space, Time and Spacetime. University of California Press. ISBN 978-0-520-03174-6. https://books.google.com/books?id=cPLXqV3QwuMC&pg=PA206.
- Sergey Stepanov (2018). Relativistic World. De Gruyter. ISBN 9783110515879. https://books.google.com/books?id=Rc6PtAEACAAJ.
- Taylor, Edwin, and John Archibald Wheeler (1992). Spacetime Physics (2nd ed.). W. H. Freeman & Co. ISBN 0-7167-2327-1.
- Tipler, Paul, and Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman & Co. ISBN 0-7167-4345-0.
Journal articles
- Alvager, T. et al. (1964). "Test of the Second Postulate of Special Relativity in the GeV region". Physics Letters 12 (3): 260–262. doi:10.1016/0031-9163(64)91095-9. Bibcode: 1964PhL....12..260A.
- Darrigol, Olivier (2004). "The Mystery of the Poincaré–Einstein Connection". Isis 95 (4): 614–26. doi:10.1086/430652. PMID 16011297.
- Wolf, Peter; Petit, Gerard (1997). "Satellite test of Special Relativity using the Global Positioning System". Physical Review A 56 (6): 4405–09. doi:10.1103/PhysRevA.56.4405. Bibcode: 1997PhRvA..56.4405W.
- Special Relativity Scholarpedia
- Rindler, Wolfgang (2011). "Special relativity: Kinematics". Scholarpedia 6 (2): 8520. doi:10.4249/scholarpedia.8520. Bibcode: 2011SchpJ...6.8520R.
External links
Original works
- Zur Elektrodynamik bewegter Körper Einstein's original work in German, Annalen der Physik, Bern 1905
- On the Electrodynamics of Moving Bodies English Translation as published in the 1923 book The Principle of Relativity.
Special relativity for a general audience (no mathematical knowledge required)
- Einstein Light An award-winning, non-technical introduction (film clips and demonstrations) supported by dozens of pages of further explanations and animations, at levels with or without mathematics.
- Einstein Online Introduction to relativity theory, from the Max Planck Institute for Gravitational Physics.
- Audio: Cain/Gay (2006) – Astronomy Cast. Einstein's Theory of Special Relativity
Special relativity explained (using simple or more advanced mathematics)
- Bondi K-Calculus – A simple introduction to the special theory of relativity.
- Greg Egan's Foundations.
- The Hogg Notes on Special Relativity A good introduction to special relativity at the undergraduate level, using calculus.
- Relativity Calculator: Special Relativity – An algebraic and integral calculus derivation for E = mc2.
- MathPages – Reflections on Relativity A complete online book on relativity with an extensive bibliography.
- Special Relativity An introduction to special relativity at the undergraduate level.
- Relativity: the Special and General Theory at Project Gutenberg, by Albert Einstein
- Special Relativity Lecture Notes is a standard introduction to special relativity containing illustrative explanations based on drawings and spacetime diagrams from Virginia Polytechnic Institute and State University.
- Understanding Special Relativity The theory of special relativity in an easily understandable way.
- An Introduction to the Special Theory of Relativity (1964) by Robert Katz, "an introduction ... that is accessible to any student who has had an introduction to general physics and some slight acquaintance with the calculus" (130 pp; pdf format).
- Lecture Notes on Special Relativity by J D Cresser Department of Physics Macquarie University.
- SpecialRelativity.net – An overview with visualizations and minimal mathematics.
- Relativity 4-ever? The problem of superluminal motion is discussed in an entertaining manner.
Visualization
- Raytracing Special Relativity Software visualizing several scenarios under the influence of special relativity.
- Real Time Relativity The Australian National University. Relativistic visual effects experienced through an interactive program.
- Spacetime travel A variety of visualizations of relativistic effects, from relativistic motion to black holes.
- Through Einstein's Eyes The Australian National University. Relativistic visual effects explained with movies and images.
- Warp Special Relativity Simulator A computer program to show the effects of traveling close to the speed of light.
- Animation clip on YouTube visualizing the Lorentz transformation.
- Original interactive FLASH Animations from John de Pillis illustrating Lorentz and Galilean frames, Train and Tunnel Paradox, the Twin Paradox, Wave Propagation, Clock Synchronization, etc.
- lightspeed An OpenGL-based program developed to illustrate the effects of special relativity on the appearance of moving objects.
- Animation showing the stars near Earth, as seen from a spacecraft accelerating rapidly to light speed.
 |
Categories: [Special relativity]
↧ Download as ZWI file | Last modified: 07/31/2024 12:10:09 | 3 views
☰ Source: https://handwiki.org/wiki/Physics:Special_relativity | License: CC BY-SA 3.0

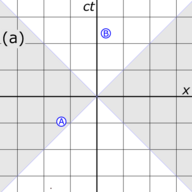


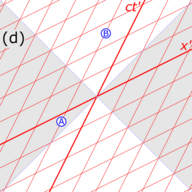

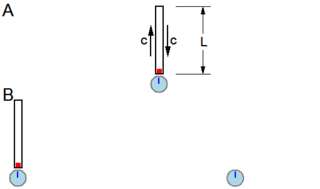
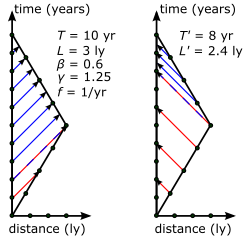

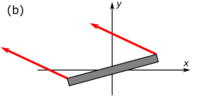
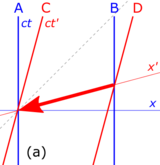
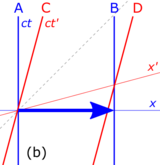

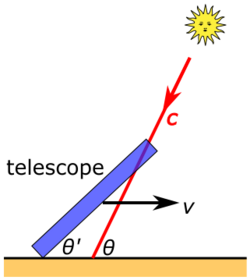

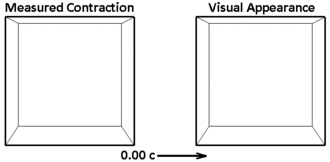

.jpg)



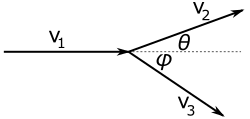



 KSF
KSF