5 (Number)

5
0 1 2 3 4 5 6 7 8 9 >> List of numbers — Integers 0 10 20 30 40 50 60 70 80 90 >>
Cardinal	5 five
Ordinal	5th fifth
Numeral system	quinary
Factorization	prime
Divisors	1, 5
Roman numeral	V
Roman numeral (Unicode)	Ⅴ, ⅴ
Arabic	٥
Arabic (Urdu)	۵
Ge'ez	፭
Bengali	৫
Chinese numeral	五，伍
Devanāgarī	५
Hebrew	ה (He)
Khmer	៥
Thai	๕
prefixes	penta-/pent- (from Greek) quinque-/quinqu-/quint- (from Latin)
Binary	101
Octal	5
Duodecimal	5
Hexadecimal	5
Vigesimal	5

5 (five) is a number, numeral, and glyph that represents the number. It is the natural number^[1] that follows 4 and precedes 6. It is an integer and a cardinal number, that is, a number that is used for counting.^[2] In addition, it is classified as a real number,^[3] distinguishing it from imaginary numbers.

Evolution of the glyph

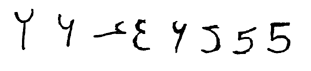
The evolution of our modern glyph for five cannot be neatly traced back to the Brahmin Indians quite the same way one can trace the glyphs for 1 to 4. The (later) Kushana and Gupta Indians had among themselves several different glyphs that bear no resemblance to the modern glyph. The Nagari and Punjabi took these glyphs and all came up with glyphs that look like a lowercase "h" rotated 180°. The Ghubar Arabs transformed the glyph in several different ways, coming up with glyphs that look more like 4s or 3s than 5s.^[4] It was from those characters that the Europeans finally came up with the modern 5, though from purely graphical evidence, it would be much easier to conclude that the modern 5 came from the Khmer. The Khmer glyph develops from the Kushana/Ândhra/Gupta numeral, its shape looking like a modern day version with an extended swirled "tail."^[4]

While the shape of the 5 character has an ascender in most modern typefaces, in typefaces with text figures the character usually has a descender, for example, in .

In mathematics

Five is between 4 and 6 and is the third prime number, after 2 and 3, and before 7. Because it can be written as 2^(2^1)+1, five is classified as a Fermat prime. 5 is the third Sophie Germain prime, the first safe prime, and the third Mersenne prime exponent. Five is the first Wilson prime and the third factorial prime, also an alternating factorial. It is an Eisenstein prime with no imaginary part and real part of the form ${\displaystyle 3n-1}$. It is also the only number that is part of more than one pair of twin primes.

Five is conjectured to be the only odd untouchable number.

The number 5 is the 5th Fibonacci number, being 2 plus 3. 5 is also a Pell number and a Markov number, appearing in solutions to the Markov Diophantine equation: (1, 2, 5), (1, 5, 13), (2, 5, 29), (5, 13, 194), (5, 29, 433), ....^[5] Whereas 5 is unique in the Fibonacci sequence, in the Perrin sequence 5 is both the fifth and sixth Perrin numbers.

5 and 6 form a Ruth-Aaron pair under either definition.

There are five solutions to Znám's problem of length 6.

Five is the second Sierpinski number of the first kind, and can be written as S2=(2^2)+1

While polynomial equations of degree 4 and below can be solved with radicals, equations of degree 5 and higher cannot generally be so solved. This is the Abel-Ruffini theorem. This is related to the fact that the symmetric group S_n is a solvable group for n ≤ 4 and not solvable for n ≥ 5.

While all graphs with 4 or fewer vertices are planar, there exists a graph with 5 vertices which is not planar: K₅, the complete graph with 5 vertices.

Five is also the number of Platonic solids.

A polygon with five sides is a pentagon. Figurate numbers representing pentagons (including five) are called pentagonal numbers. Five is also a square pyramidal number.

Five is the only prime number to end in the digit 5, because all other numbers written with a 5 in the ones-place under the decimal system are multiples of five. As a consequence of this, 5 is in base 10 a 1-automorphic number.

Vulgar fractions with 5 or 2 in the denominator do not yield infinite decimal expansions, as is the case with most primes, because they are prime factors of ten, the base. When written in the decimal system, all multiples of 5 will end in either 5 or 0.

There are five Exceptional Lie groups.

Numbering systems

• In binary, code five is 101
• In ternary, code five is 12
• In quaternary, numeral system code five is 11
• In quinary, five is 10; and in senary, code and all codes above (such as decimal, duodecimal and vigesimal) five is 5.
• The Roman numeral for five is V, which comes from a representation of an outstretched hand.
• In the Arabic alphabet, ٥‎ (hāʼ) has numerical value of 5.
• In the Greek alphabet, ε (epsilon) has numerical value of 5.
• In the Hebrew alphabet, ה (heh) has numerical value of 5.
• In the Cyrillic alphabet, Е has numerical value of 5.
• In the Glagolitic alphabet, 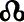(dobro) has numerical value of 5.
• The kanji and Chinese character for five are both 五, and its formal writing in Chinese is 伍 (pinyin wǔ).

List of basic calculations

Multiplication

Multiplication	1	2	3	4	5	6	7	8	9	10
${\displaystyle 5\times x}$	5	10	15	20	25	30	35	40	45	50

Multiplication	11	12	13	14	15	16	17	18	19	20
${\displaystyle 5\times x}$	55	60	65	70	75	80	85	90	95	100

Multiplication	21	22	23	24	25		50	100	1000
${\displaystyle 5\times x}$	105	110	115	120	125		250	500	5000

Division

Division	1	2	3	4	5	6	7	8	9	10
${\displaystyle 5\div x}$	5	2.5	${\displaystyle 1.{\overline {6}}}$	1.25	1	${\displaystyle 0.8{\overline {3}}}$	${\displaystyle 0.{\overline {7}}1428{\overline {5}}}$	0.625	${\displaystyle 0.{\overline {5}}}$	0.5
${\displaystyle x\div 5}$	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2

Division	11	12	13	14	15
${\displaystyle 5\div x}$	${\displaystyle 0.{\overline {4}}{\overline {5}}}$	${\displaystyle 0.41{\overline {6}}}$	${\displaystyle 0.{\overline {3}}8461{\overline {5}}}$	${\displaystyle 0.3{\overline {5}}7142{\overline {8}}}$	${\displaystyle 0.{\overline {3}}}$
${\displaystyle x\div 5}$	2.2	2.4	2.6	2.8	3

Exponentiation

Exponentiation	1	2	3	4	5	6	7	8	9	10
${\displaystyle 5^{x}\,}$	5	25	125	625	3125	15625	78125	390625	1953125	9765625
${\displaystyle x^{5}\,}$	1	32	243	1024	3125	7776	16807	32768	59049	100000

Exponentiation	11	12	13
${\displaystyle 5^{x}\,}$	48828125	244140625	1220703125
${\displaystyle x^{5}\,}$	161051	248832	371293

In science

Chemistry

• The atomic number of boron is five.
• The smallest atomic mass number (the sum of protons and neutrons) for which no stable isotopes exist for any element.

Biology

• Humans and other primates have five digits on each hand and five toes on each foot.
• Five is the number of appendages on most starfish, which exhibit pentamerism.

Meteorology

• The most destructive known tornadoes rate an F-5 on the Fujita scale.
• The most destructive known hurricanes rate as Category 5 on the Saffir-Simpson scale.

Astronomy

• Messier object M5, a magnitude 7.0 globular cluster in the constellation Serpens.
• The Saros number of the solar eclipse series which began on April 4, 2720 B.C.E. and ended on May 24, 1422 B.C.E. The duration of Saros series 5 was 1298.17 years, and it contained 73 solar eclipses.^[6]
• The Saros number of the lunar eclipse series which began on December 22, 2455 B.C.E. and ended on March 24, 1084 B.C.E. The duration of Saros series 5 was 1370.29, and it contained 77 lunar eclipses.^[7]
• The Roman numeral V (usually) stands for the fifth-discovered satellite of a planet or minor planet (such as Jupiter V).
• The Roman numeral V stands for dwarfs (main sequence stars) in the Yerkes spectral classification scheme.

In technology

• Five is the resin identification code used in recycling to identify polypropylene.
• In radio communication, the term "Five by five" is used to indicate perfect signal strength and clarity.
• The Pentium, coined by Intel Corporation, is a fifth-generation x86 architecture microprocessor.
• On almost all devices with a numeric keypad such as telephones and computers, the 5 key has a raised dot or raised bar to make dialing easier. Persons who are blind or have low vision find it useful to be able to feel the keys of a telephone. All other numbers can be found with their relative position around the 5 button. (On computer keyboards, the 5 key of the numpad has the raised dot or bar, but the 5 key that shifts with the % symbol does not.)
• 5 is a common number of gears for automobiles with manual transmission.

In religion

Judaism

• The Torah contains five books: Genesis, Exodus, Leviticus, Numbers, and Deuteronomy. They are collectively called the Five Books of Moses, the Pentateuch (Greek for "five containers," referring to the scroll cases in which the books were kept), or Humash (חומש, Hebrew for "fifth").
• The book of Psalms is arranged into five books, paralleling the Five Books of Moses.
• The Khamsa, an ancient symbol shaped like a hand with five fingers, is used as a protective amulet by Jews.

Christianity

• In Greek Orthodox Christian mysticism, the number 5 symbolizes the Holy Spirit as the bearer of all life. In the monastic tradition of Mount Athos there exists a "hymn" to the Holy Spirit composed entirely and solely of repetitions of the word "pente" (Greek for "five")

Islam

• There are five basic "pillars" of Islam.
• Muslims pray to Allah five times a day *In Islam, particularly Shia Islam, the Panjetan or the Five Holy Purified Ones are the members of Muhammad's family including: Muhammad, Ali, Fatima, Hasan, Husayn and is often symbolically represented by an image of the Khamsa.

Other religions

• The five sacred Sikh symbols prescribed by Guru Gobind Singh are commonly known as Panj Kakars or the "Five Ks" because they start with letter K representing Kakka in the Punjabi language. They are: Kesh (unshorn hair), Kangha (the comb), Kara (the steel bracelet), Kachh (the soldiers shorts), and Kirpan (the sword).
• According to some traditions of Maya mythology, we are now living in the Fifth World.
• In East Asian tradition, there are five elements: Water, fire, earth, wood, and metal. The Japanese names for the days of the week, Tuesday through Saturday, come from these elements via the identification of the elements with the five planets visible with the naked eye. Also, the traditional Japanese calendar has a five-day weekly cycle that can be still observed in printed mixed calendars combining Western, Chinese-Buddhist and Japanese names for each weekday.
• In some cultures there are five cardinal directions, including the center.
• In Cantonese, "five" sounds like the word "not" (symbol: 唔). When five appears in front of a lucky number, for example, "58," the result is considered unlucky.
• In Discordianism, 5 is seen as a very important number as demonstrated in the Law of Fives and The Pentabarf, which contains five rules. Each page of the Principia Discordia, the primary religious document in Discordianism, is also labeled with 5 digits.

In music

• A perfect fifth is the most consonant harmony, and is the basis for most western tuning systems.
• Modern musical notation uses a musical staff made of five horizontal lines.
• Using the Latin root, five musicians are called a quintet, for example, the Jackson Five. (In an episode of Will & Grace guest-starring Janet Jackson, she declared that 5 is a mystical number and for that reason she must have precisely 5 backup dancers).
• The Five is the name of a nineteenth-century Russian Group of nationalistic composers who included César Cui, Aleksandr Borodin, Mily Balakirev, Modest Mussorgsky, and Nikolay Rimsky-Korsakov.
• The name of the band The Fifth Dimension implies that they are transcending beyond even the fourth dimension (time) into a new inner dimension.
• Take Five is a famous jazz standard composed by Paul Desmond. It counts five beats per bar.
• The number of completed, numbered piano concertos of Ludwig van Beethoven and Camille Saint-Saëns.
• In harmonics—The fifth partial (or 4th overtone) of a fundamental has a frequency ratio of 5/1 to the frequency of that fundamental. This ratio corresponds to the interval of 2 octaves + a pure major third. Thus, the interval of 5/4 is the interval of the pure third. A major triad chord when played in just intonation (most often the case in a cappella vocal ensemble singing), will contain such a pure major third.

In sports

• The number of players of a basketball team on the court at a given time.
• Also used in basketball to represent the position of center.
• The Olympic Games have five interlocked rings as their symbol, representing the number of inhabited continents represented by the Olympians (counting North America and South America as one continent).
• The number of kyu (pupil) grades in judo
• In rugby union, the number of the lock forward who usually jumps at number 4 in the line-out. It is also the number of points awarded for a try.
• In rugby league, the number of the left wing, and also the number of tackles the attacking team has to score a try before the handover.
• In baseball, five represents the third baseman's position.
• In hockey, the area between the goaltender's legs is known as the five-hole.

Miscellaneous fields

• Five is the number of oceans in the world.
• The five senses are sight, smell, sound, touch and taste.
• The five basic tastes are sweet, salty, sour, bitter and umami.
• In various early cultures, the universe was thought to be comprised of five classical elements: water, earth, air, fire, and ether.
• Pentameter is verse with five repeating feet per line; iambic pentameter was the most popular form in Shakespeare.
• In the United States legal system, the Fifth Amendment to the United States Constitution can be referred to in court as "pleading the fifth," absolving the defendant from self-incrimination.
• Five is the number of permanent members with veto power on the UN Security Council.
• Five is the least number of justices needed to make a majority decision in the U.S. Supreme Court.
• Five babies born at one time are quintuplets. The most famous set of quintuplets were the Dionne Quintuplets born in the 1930s.
• Quintessence, meaning "fifth element," refers to the elusive fifth element that completes the basic four elements (water, fire, air and earth).
• Five is the number of dots in a quincunx.
• There are five points in a pentagram.
• The Garden of Cyrus 1658, by Sir Thomas Browne is a Pythagorean Discourse based upon the number 5.
• The word "punch" comes from the Hindi word for five. Being true to the designation of punch, the drink Five Alive is named for its five ingredients.
• Five is an informal term for the British Security Service, MI5.
• There are five vowels in the English alphabet: A, e, i, o and u.

See also

• Arithmetic
• Integer
• Number

Notes

References

ISBN links support NWE through referral fees

• Flegg, Graham. Numbers: Their History and Meaning. Mineola, NY: Dover Publications, 2002. ISBN 0486421651
• Ifrah, Georges. The Universal History of Numbers: From Prehistory to the Invention of the Computer. Translated by David Bellos et al. New York: Wiley, 2000. ISBN 0471393401
• McLeish, John. The Story of Numbers: How Mathematics Has Shaped Civilization. New York: Fawcett Columbine, 1994. ISBN 0449909387
• Menninger, Karl. Number Words and Number Symbols: A Cultural History of Numbers. New York: Dover Publications, 1992. ISBN 0486270963
• Wells, D. G. The Penguin Dictionary of Curious and Interesting Numbers. London: Penguin Books, 1998. ISBN 0140261494

External links

All links retrieved October 7, 2022.

• The Number 5
• Properties of the number 5
• Number 5 in Math