Machine Learning In Physics

Applying classical methods of machine learning to the study of quantum systems is the focus of an emergent area of physics research. A basic example of this is quantum state tomography, where a quantum state is learned from measurement.^[1] Other examples include learning Hamiltonians,^[2][3] learning quantum phase transitions,^[4][5] and automatically generating new quantum experiments.^[6][7][8][9] Classical machine learning is effective at processing large amounts of experimental or calculated data in order to characterize an unknown quantum system, making its application useful in contexts including quantum information theory, quantum technologies development, and computational materials design. In this context, it can be used for example as a tool to interpolate pre-calculated interatomic potentials^[10] or directly solving the Schrödinger equation with a variational method.^[11]

Applications of machine learning to physics

Noisy data

The ability to experimentally control and prepare increasingly complex quantum systems brings with it a growing need to turn large and noisy data sets into meaningful information. This is a problem that has already been studied extensively in the classical setting, and consequently, many existing machine learning techniques can be naturally adapted to more efficiently address experimentally relevant problems. For example, Bayesian methods and concepts of algorithmic learning can be fruitfully applied to tackle quantum state classification,^[12] Hamiltonian learning,^[13] and the characterization of an unknown unitary transformation.^[14][15] Other problems that have been addressed with this approach are given in the following list:

• Identifying an accurate model for the dynamics of a quantum system, through the reconstruction of the Hamiltonian;^[16][17][18]
• Extracting information on unknown states;^{[19][20][21][12][22][1]}
• Learning unknown unitary transformations and measurements;^[14][15]
• Engineering of quantum gates from qubit networks with pairwise interactions, using time dependent^[23] or independent^[24] Hamiltonians.
• Improving the extraction accuracy of physical observables from absorption images of ultracold atoms (degenerate Fermi gas), by the generation of an ideal reference frame.^[25]

Calculated and noise-free data

Quantum machine learning can also be applied to dramatically accelerate the prediction of quantum properties of molecules and materials.^[26] This can be helpful for the computational design of new molecules or materials. Some examples include

• Interpolating interatomic potentials;^[27]
• Inferring molecular atomization energies throughout chemical compound space;^[28]
• Accurate potential energy surfaces with restricted Boltzmann machines;^[29]
• Automatic generation of new quantum experiments;^[6][7]
• Solving the many-body, static and time-dependent Schrödinger equation;^[11]
• Identifying phase transitions from entanglement spectra;^[30]
• Generating adaptive feedback schemes for quantum metrology and quantum tomography.^[31][32]

Variational circuits

Variational circuits are a family of algorithms which utilize training based on circuit parameters and an objective function.^[33] Variational circuits are generally composed of a classical device communicating input parameters (random or pre-trained parameters) into a quantum device, along with a classical Mathematical optimization function. These circuits are very heavily dependent on the architecture of the proposed quantum device because parameter adjustments are adjusted based solely on the classical components within the device.^[34] Though the application is considerably infantile in the field of quantum machine learning, it has incredibly high promise for more efficiently generating efficient optimization functions.

Sign problem

Machine learning techniques can be used to find a better manifold of integration for path integrals in order to avoid the sign problem.^[35]

Fluid dynamics

Physics discovery and prediction

Illustration of how an AI learns the basic fundamental physical concept of 'unchangeableness'^[39]

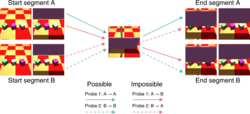
A deep learning system was reported to learn intuitive physics from visual data (of virtual 3D environments) based on an unpublished approach inspired by studies of visual cognition in infants.^[40][39] Other researchers have developed a machine learning algorithm that could discover sets of basic variables of various physical systems and predict the systems' future dynamics from video recordings of their behavior.^[41][42] In the future, it may be possible that such can be used to automate the discovery of physical laws of complex systems.^[41] Beyond discovery and prediction, "blank slate"-type of learning of fundamental aspects of the physical world may have further applications such as improving adaptive and broad artificial general intelligence.^{[additional citation(s) needed]} In specific, prior machine learning models were "highly specialised and lack a general understanding of the world".^[40]

See also

• Quantum computing
• Quantum machine learning
• Quantum algorithm for linear systems of equations
• Quantum annealing
• Quantum neural network

References

0.00 (0 votes)