Economics Lecture Five
 From Conservapedia
From Conservapedia Economics Lectures - [1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12 - 13 - 14]
Much of this lecture is devoted to review, and we also learn about the powerful Coase theorem. The homework this week includes a quiz that covers the entire course so far.
By now you may have noticed that there is a style to economics: simple concepts are studied very carefully. Patience is essential to solving economic problems correctly. Unlike history or science, it helps in economics to be extremely careful when first considering a problem. Haste or sloppiness at the outset of trying to solve a problem can lead to unnecessary mistakes.
Economics consists of making simple observations about complex situations in order to derive powerful results. There may be many things that are unknown or uncertain about a situation, but economics looks at what can be determined and then derives as much as possible from what is known. For example, one might ask an economist what he can say about public school classes. Most people might respond, "I can't say anything about them without knowing more information." But an economist thinks about what can be said despite the lack of knowledge of all the details. The economist might say that we do know this: public school classes censor prayer and avoid discussion of the Bible. From that simple observation, an economist might draw a powerful conclusion: students are completely missing out on the central source of wisdom and comfort.
Contents
Efficiency[edit]
Imagine what your day is like as President of the widget factory. You arrive to work earlier than everyone else, because you care the most about the success of your company. During the workday you walk through your factory to see how things are going. You see employees chatting at the water cooler, talking to their friends on the phone, or not showing up for work at all. This irritates you because you are paying for their time. You tell them to get back to work.
You also see equipment sitting idle for various reasons. That annoys you too. You paid for the equipment, or you are renting it, but it is not helping your business by sitting idle. You want to return or sell it, or find a way to make it useful.
Less easy to see are the wasted opportunity costs. Perhaps your assembly line could be making a different kind of widget that would be more profitable than the one you are making.
All your concerns can be summed in one economic term: “efficiency”. Efficiency is the maximum possible productivity at any given time. It consists of the least amount of wasted time, effort or money. There is no wasted opportunity cost in an efficient operation.
This economic term (“efficiency”) has the same meaning as its common everyday usage. “It was an inefficient use of my time to sit here all morning waiting for you!” “Try to do your chores more efficiently so that you can finish sooner.” “She finishes her homework faster than you because she works more efficiently.”
Generally, maximum efficiency is desired and people want to avoid wasted time, materials, effort, and expense. However, there is a significant obstacle to true efficiency: transaction costs. Recall that “transaction costs” are all the incidental expenses that a consumer must spend to acquire a good. One textbook defines transaction costs as “the time, effort, and expense that go into the purchase of a good.”[1] Nobel laureate Ronald Coase, discussed later in this lecture, describes “transaction costs” as simply the “costs of using the market.”
If you love the homemade ice cream at your favorite restaurant, then you have to spend the time and money driving there, waiting for a table, tipping the waitress, paying the sales tax, etc. All you wanted was the homemade ice cream, but many transaction costs stand in the way of a perfectly efficient transaction.
One day you may want to buy a house. Ideally, you would like to drive up to the house you want and pay the owner directly, and then move in. But in reality, there are transaction costs in buying a house. These include finding what you want, bargaining over the price, paying a real estate broker and attorney, and so on. Those transaction costs drive up the price of the house, and create inefficiencies. Some additional transaction costs are imposed by governmental regulations.
Review: Elasticity[edit]
In Lecture Three we learned about "elasticity". Let's define it again: elasticity is the responsiveness in demand for a particular good due to changes in a variable such price or income.[2]
The concept of elasticity is worth learning well. Many questions on an economics exam (such as the CLEP) ask about elasticity.
There are two types of elasticity of demand:
- price elasticity of demand
- income elasticity of demand
Keep these different types of elasticity separate: price elasticity is the change in demand due to a change in the price of the good, while income elasticity is the change in demand due to a change in the income of the buyer.
Price Elasticity (review)[edit]
Price elasticity of demand is the change in the quantity demanded by the public for a particular good due to a change in its price. Its symbol is "Ped", for "Price elasticity of demand." This term is used to answer this question: if the price of gasoline increases, how does the demand for gasoline change? It decreases due to the Law of Demand, but the price elasticity tells us how much it decreases due to a price increase. Specifically, price elasticity is the percentage change in quantity demanded, divided by the percentage change in the price of the good. If the percent change in quantity demanded is more than the percent change in price, then the good is considered "elastic". If the percent change in quantity demanded is less than the percent change in price, then the good is considered "inelastic". The Law of Demand means that price elasticity is always negative, but for convenience everyone uses the absolute value (positive value) without the minus sign.
Price elasticity of demand is important because it tells us whether the owner's overall revenue goes up or down due to a price change. Revenue is price times quantity, and when price goes up then quantity goes down, and we need to know the price elasticity to know what happens to the overall P x Q (price times quantity, which is the revenue).
Mathematically, price elasticity is as follows:
Cross Elasticity[edit]
Once you fully understand price elasticity of demand, then it is easy to understand the concept of "cross elasticity of demand." Cross elasticity of demand is the percent change in demand of one good due to a change in the price of a different good. The two goods are either substitutes or complements for each other, which makes their cross elasticity useful. The symbol for cross elasticity of demand is "Xed", with "X" representing the "cross" and "ed" representing the "elasticity of demand."
Mathematically, cross elasticity is as follows:
Note that cross elasticity is different from price elasticity in that cross elasticity is comparing the change in demand for one good in response to the change in price of another good.
If the two goods (X and Y) are complements, then the cross elasticity is negative just as the price elasticity of a good is. Ketchup is a complement for french fries, and if the price of french fries increases, then people will eat fewer french fries and less ketchup. Hence the demand for ketchup will decrease and its cross elasticity with respect to french fries is negative.
If the two goods (X and Y) are substitutes, then the cross elasticity is positive. Potato chips are a substitute for french fries, and if the price of french fries increases, then people will eat fewer french fries and more potato chips. Hence the demand for potato chips will increase and its cross elasticity with respect to french fries is positive.
Expect a question on an exam which provides two goods and asks whether their cross elasticity is positive or negative. The correct answer will depend on whether the goods are complements (then the answer is "negative") or substitutes (then the answer is "positive").
Income Elasticity (review)[edit]
Income elasticity of demand is the change in the quantity demanded by the public for a particular good due to a change in income. Stated another way, income elasticity is the responsiveness in demand for a good due to a change in the buyers' income. Its symbol is "Yed", because "Y" is a symbol for income, and "ed" refers to "elasticity of demand."
In calculating elasticity, the numerator is the same for both price and income elasticity: it is the percent change in quantity demanded for the good. But the denominator is different for these two elasticities: the denominator for price elasticity is the percent change in price of the good, while the denominator for income elasticity is the percent change in income for the buyers.
Unlike price elasticity, income elasticity can be either positive or negative, depending on the good. For a "normal" good, income elasticity is positive; for an "inferior" good, it is negative. Inferior goods are rare: they have a decrease in demand when income by the public increases. Usually demand for goods increase as income by the public increases, hence the name "normal good" to describe them.
Normal goods are necessities or luxuries, depending on their elasticity: necessities are inelastic (elasticity less than 1), and luxuries are elastic (elasticity greater than 1). Notice that "necessity" and "luxury" goods are defined in terms of income elasticity, not in terms of price elasticity.
This table is a useful study guide for income elasticity:
| Yed | Normal or Inferior? | Elastic or Inelastic? | Necessity or Luxury? |
|---|---|---|---|
| Yed = -0.5 | inferior | inelastic | neither necessity nor luxury |
| Yed = 0.6 | normal | inelastic | necessity |
| Yed = -1.9 | inferior | elastic | neither necessity nor luxury |
| Yed = 3.5 | normal | elastic | luxury |
Mathematically, income elasticity is as follows:
Supply Elasticity[edit]
One more and we're done. The price elasticity of supply is the percent change in quantity supplied divided by the percent change in price for the good. Mathematically, that is:
If the supply elasticity (Pes) is inelastic (less than 1), then it is difficult for suppliers to react quickly to a change in price. If Pes is elastic (more than 1), then suppliers can react quickly to a change in price, as in supplying more goods when the price increases.
Marginal Cost and Marginal Revenue[edit]
Two of the most important concepts in economics are marginal cost and marginal revenue.
Marginal cost is the additional cost to produce one more unit. It includes only the additional cost, and not any costs to produce anything else. If, for example, you drove to the grocery store and then saw another store a half mile up the road, the marginal cost of driving to that store would be only the additional gas and time and wear and tear on the car for going the extra half mile. The marginal cost would not include the original cost of the car, or taking off time from work, or anything other than the extra cost of going that extra half mile.
Similarly, the marginal revenue is the additional revenue received by a business from selling one more unit. It equals the price of the unit, because revenue is P x Q, and for one more unit Q (quantity) is 1.
Imagine yourself as an owner of a business. As long as marginal revenue is larger than marginal cost, then you will want to sell more and more units. But once marginal revenue falls just below your marginal cost, then you lose money for each additional unit. You will lose money in selling more goods at that point.
An owner sells as many goods as he can until marginal revenue decreases to the level of his marginal cost. At that point he does not make any more money selling goods, and he stops selling additional goods.
Example: a grocery store owner considers how late he should keep his store open at night. His marginal cost includes electricity and wages for employees. His marginal revenue includes the groceries purchased by the late-night shoppers. Once the volume of groceries late at night decreases to the point where his marginal revenue from those sales dips below his marginal cost for keeping the store open, he closes his store for the night.
The Coase Theorem[edit]
The most-cited article in all of economics[3] is “The Problem of Social Cost,” published by Professor Ronald H. Coase in 1960. It describes what later became known as the “Coase theorem,” a fundamental conservative insight about entitlements and property rights. Though criticized for thirty years by professors who disliked its implications, this theorem was finally recognized by the 1991 Nobel Prize of Economics, of which Professor Coase was the sole recipient. (An unshared Nobel Prize awarded to only one recipient is rare.) Some oppose this theorem, despite its truth, and economists have even called Professor Coase names in criticism.[3]
The Coase Theorem Explained[edit]
Like Isaac Newton, who invented calculus in order to do his work on physics, Ronald Coase first invented the new concept of “transaction costs” to lay the groundwork for his insight. As we have explained, “transaction costs” consist of the time, money, and effort someone loses in obtaining what he wants. Law professor Richard Epstein tersely summed up the meaning of “transaction costs” in one word: “friction.”[3] Coase’s Nobel Prize was partly based on his discovery and development of this new concept, and the committee conferring the prize (the Royal Swedish Academy of Sciences) likened this to the discovery of a new set of elementary particles in physics.
Once “transaction costs” were discovered and described, Coase’s insight became possible. The Coase theorem states that in the absence of transaction costs, an efficient or optimal economic result occurs regardless of who owns the property rights. The free market guarantees the efficient outcome regardless of who owns what, because there are incentives to bargain towards the efficient result until it is achieved. This is true even for activities that generate “negative externalities” (harm to others); freedom to negotiate will enable all affected to bargain towards the most efficient output.
Restated another way, if property rights are well-defined and transaction costs are zero, then the most efficient or optimal economic activity will occur regardless of who holds the rights, because negotiation and market transactions will ensure the optimal allocation and use of property in a free market.
Chicago federal trial judge Milton Shadur explained the legal meaning of this theorem. “So long as the rule of law is known when parties act, the ultimate economic result is the same no matter which way the law has resolved the issue.”[4] Whether the law gives an entitlement to a rich man or a poor one, the economic activity will be the same, assuming people can bargain freely with each other.
An oversimplification of this concept is Ralph Waldo Emerson’s famous statement that if a man can “make a better mouse-trap … [then] the world will make a beaten path to his door.” Assuming people can buy and sell without regulatory or other barriers, it does not matter who invents the mousetrap or who obtains legal rights to it. The free market will ensure that the better mousetrap is sold to the public for the benefit of all involved.
The meaning of Coase’s insight for government regulation was clear. A society is better off by simply assigning property rights, reducing transaction costs, and getting out of the way so that the market process can reach its most efficient result. Government regulations that add transaction costs hurt efficiency and prosperity. In response to the question “What’s an example of bad regulation?,” Coase replied, “I can’t remember one that’s good.”
The Most Famous Dinner in the History of Economics[5][edit]
Initially Professor Coase’s theory was criticized, even by economists. In 1959 Coase, then in the economics department at the University of Virginia, published an early version in an article concerning allocation of the radio frequency spectrum. Coase proposed that the Federal Communications Commission reject its bureaucratic procedures for assigning licenses and simply sell frequencies in the spectrum to the highest bidders. Coase elaborated on his theory in his article, but every economist at the University of Chicago objected. Even though the Chicago economists were predisposed towards free markets, they thought Coase had erred.
These economists wanted the truth, and they invited Coase to a friendly dinner at the home of a conservative economist named Aaron Director. Milton Friedman and George Stigler were among those in attendance who thought Coase had erred. When hors d’oeuvres were served, the vote was 20 against Coase’s theory and only Coase in favor of it. As the two-hour discussion proceeded, it became like a scene from the famous movie 12 Angry Men. One by one, bit by bit, the great economists came over to Coase’s side as their objections were resolved. By the end their leader, Milton Friedman himself heroically admitted that he had been wrong and Coase was right. To his enormous credit, Professor Friedman then became an energetic champion of Coase’s theory.
The dinner attendees thanked Coase and invited him to write up his theory more fully for a new publication called the Journal of Law and Economics, and Coase's article became the most cited paper in all of economics.
The Man Behind the Coase Theorem[edit]
Who is this man behind this revelation? It took an unconventional education to bring forth this insightful work. Professor Ronald Coase, born in 1910 in England, suffered from a physical handicap as a youngster and thus could not attend regular school. He had to wear leg braces and was eventually enrolled in a school for “physical defectives.” But that school was managed by the same organization that ran the school for “mental defectives,” and Coase later explained that there was “some overlapping in the curriculum.”[6] As a result, Coase spent his days in basket-weaving classes, and was deprived of any formal academic instruction until age 10.
He eventually found his way to the London School of Economics, where he was a socialist until his senior year, when he enrolled in a seminar taught by Professor Arnold Plant. That course was devoted to the “invisible hand” and featured stimulating discussions without any readings. It changed Coase’s life, as he embraced the power of the free market.
Later he emigrated to the United States and eventually joined the faculty at the University of Chicago. His work almost never included a mathematical equation or formula, contrary to the modern trend in economics. To this day many in the field of law and economics, which Coase helped found, pursue quantification that he would never have done himself.
Professor Coase’s breakthrough was analogous to that of mathematician Kurt Gödel. Both deflated the arrogance of their colleagues, and as a result both received a chilly reception from their peers.
Implications of the Coase Theorem[edit]
In public policy, the Coase theorem implies that greater efficiency and prosperity can be obtained by reducing and eliminating transaction costs. Bureaucratic hurdles erected by government and the legal system increase transaction costs and reduce efficiency and prosperity. Society as a whole would be better off if transaction costs were minimized. Wealth is lost by impeding the ability of people to negotiate private contracts among themselves. The role of government to increase prosperity should focus on lowering transaction costs, not raising them.
Transaction costs are particularly large in health care, where patients and physicians must waste massive amounts of time determining how much a procedure costs, whether a third party will pay for it, and obtaining payment from that third party (such as government or an insurance company). In some cases the transaction costs are even infinite, as bureaucrats try to prohibit private contracts entirely for legitimate services. Canada forbids paying privately for medical services, requiring everyone to depend on government controls.
The Coase theorem demonstrates that these transaction costs detract from overall wealth and efficient economic behavior. Legal impediments to private contracting for medical services should be removed, as such interference frustrates the ability to reach economically optimal results. The best that government can do in controlling medical costs is simply to remove the transaction costs and get out of the way so that the parties, patients and physicians can negotiate optimal arrangements.
The Coase theorem also provides economic justification for adhering to Rule of Law, and rejecting an “evolving” Constitution. As Judge Shadur observed above, as long as there is a clear Rule of Law it does not matter to prosperity where that rule assigns the rights. Often the best courts can do is embrace the Rule of Law, and then get out of the way. Changing rules midstream, as in arbitrarily taking one’s property, is economically harmful.
There are mind-bending implications of the Coase theorem. Money itself is a property right, and that property will also be allocated to its most efficient uses regardless of who controls it, assuming rational behavior and no transaction costs. Judge Shadur explained above that the Coase theorem means “the ultimate economic result is the same no matter which way the law has resolved the issue,” and likewise the economic result is the same no matter which rational person has the property right to the wealth. Bill Gates may control $100 billion or so, but the best use of that money is dictated by demand in the free market. If Gates decides to spend the money in a way contrary to its most efficient uses in the free market, then he is wasting his own money and it is his loss.
The Coase theorem even justifies the famous observation by Jesus that we “will always have the poor among” us. Attempts by government to reduce the gap between the rich and the poor result in more transaction costs, which prevent future success. These transaction costs include higher taxes and greater regulation. The more transaction costs are injected into the system, the more inefficient it becomes, and society is worse off overall. The only way government can eliminate the poor (relative to the rich) is by imposing transaction costs that make everyone poorer. Redistributing wealth is like using a leaky bucket to transfer water from one place to another.
Assignment[edit]
Read and, if necessary, reread the above lecture. Then answer the following six questions:
1. Suppose the cross elasticity of demand for goods A and B is +3.8, and for goods X and Y is -2.7. What can you conclude about the relationship of the goods A and B, and of X and Y (i.e., are they substitutes or complements)?
2. Suppose it costs you $500 to make each of your first 5 units, then $200 to make each of your next 5 units, and then $100 to make each of your next 5 units. Costs do not decrease further for you. What is the marginal cost for you to make another unit, after you have made 15 units? What is your overall average cost per unit after you make your 16th unit? Compare the two and comment on how whether they are equal, and why.
3. Suppose your annual income increases from $20,000 to $25,000. Suppose your demand for steak increases by 10% and your demand for fast food hamburgers decreases by 5%. Which type of goods are steak, and which type are hamburgers?
4. What does an owner do when his marginal revenue exceeds his marginal cost? Explain, including what will eventually happen to the marginal revenue compared with the marginal cost for the owner.
5. What does the Coase theorem say about the desirability, and the effect, of government regulations that increase transaction costs?
6. Take the online 10-question quiz at www.conservaget.com . This quiz covers the basic concepts learned in our entire course so far. If you have a smart phone such as an iPhone or Android, this quiz should work on that too. Your score is recorded electronically but also include the score as your answer to this question (e.g., 8 out of 10).
Honors[edit]
7. Write a brief (100 words is fine) essay about an implication or consequence of the Coase theorem.
References[edit]
- ↑ Spencer, Contemporary Economics, at p. D-53.
- ↑ There is also an elasticity of supply of a particular good that we'll mention below.
- ↑ 3.0 3.1 3.2 http://www.boston.com/globe/search/stories/nobel/1991/1991i.html
- ↑ Coltman v. Commissioner, 980 F.2d 1134, 1137 (7th Cir. 1992).
- ↑ Warsh D., Knowledge and the Wealth of Nations: A Story of Economic Discovery 299 (2006).
- ↑ http://www.reason.com/news/printer/30115.html
Categories: [Economics lectures]
↧ Download as ZWI file | Last modified: 02/24/2023 05:56:05 | 61 views
☰ Source: https://www.conservapedia.com/Economics_Lecture_Five | License: CC BY-SA 3.0
 ZWI signed:
ZWI signed: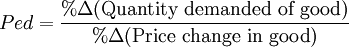
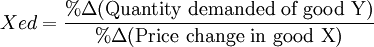
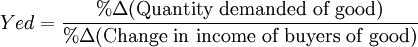
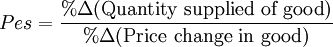
 KSF
KSF