Black-Scholes

The Black-Scholes Model[edit]

The Black-Scholes model for a stock price assumes that the stock price follows geometric Brownian motion with constant drift and volatility. More precisely, if S(t) the stock price at time t, then

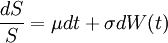
where 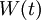is a standard Weiner stochastic process.

Loosely speaking, this means that the return 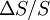of the stock over a very small time interval 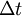can be viewed as a normal random variable with mean 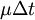and variance 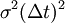. One can make this notion precise by invoking the concepts from the Ito calculus.

The Black-Scholes Formula[edit]

The Black-Scholes pricing formula for a European call option can be deduced from the Black-Scholes model for a stock price. A European call option on a stock with strike price 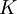and time to maturity 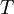is a financial contract that gives the holder the option, but not the obligation, to purchase the stock for price 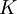at time 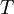. In other words, a European call on the stock S is a contract that provides a single pay-off of

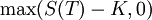
at time 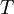. Let 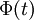denote the fair value of this contract at time 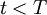. In deriving a formula for 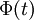, Black and Scholes' key insight was that by forming a portfolio with the exact right balance of 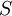and the call option, one can completely eliminate risk associated to movements in the stock price 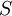. Moreover, the resulting portfolio, being risk-free, has to grow at the risk free rate. These observations implied that the fair price of the call option had to satisfy the differential equation:

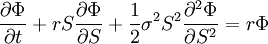
where 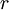is the continuously compounded risk-free interest rate, and 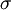is the volatility of the stock. The solution to this differential equation, satisfying the boundary condition

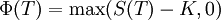
is given by:

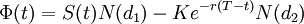
Here 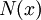is the cumulative normal distribution function,

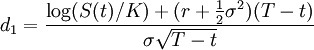
and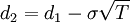

This is the famous Black-Scholes formula for the price of a European call. Note that all the variables except for 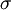can be observed in directly in the market at time 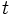. The volatility, 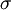of the stock must be estimated using either statistical data, or inferred from the price of options being sold in the market.