Cauchy Sequence
 From Conservapedia
From Conservapedia 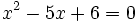
|
This article/section deals with mathematical concepts appropriate for a student in mid to late high school. |
- The reader should be familiar with the material in the Limit (mathematics) page.
A Cauchy sequence (pronounced KOH-she) is an infinite sequence that converges in a particular way. This type of convergence has a far-reaching significance in mathematics. Cauchy sequences are named after the French mathematician Augustin Cauchy (1789-1857).
There is an extremely profound aspect of convergent sequences. A sequence of numbers in some set might converge to a number not in that set. The famous example of this is that a sequence of rationals might converge, but not to a rational number. For example, the sequence
- 1.4
- 1.41
- 1.414
- 1.4142
- 1.41421
consists only of rational numbers, but it converges to 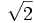 , which is not a rational number. (See real number for an outline of the proof of this.)
, which is not a rational number. (See real number for an outline of the proof of this.)
- The sequence given above was created by a computer, and it could be argued that we haven't really exhibited the sequence. But we can put such a sequence on a firm theoretical footing by using the Newton-Raphson iteration. This would give us
- so that
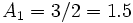
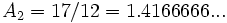
- ...
- These aren't the same as the sequence given previously, but they are all rational numbers, and they converge to
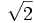 .
.
So if we lived in a world in which we knew about rational numbers but had never heard of the real numbers (the ancient Greeks sort of had this problem) we wouldn't know what to do about this. Recall that, for a sequence (an) to converge to a number A, that is
we would need to use the definition of a limit—we would need a number A such that, for every ε > 0, there is an integer M such that, whenever 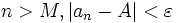 .
.
There is no such rational number A.
But there is clearly a sense in which 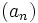 converge. The definition of Cauchy convergence is this:
converge. The definition of Cauchy convergence is this:
- A sequence
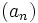 converges in the sense of Cauchy (or is a Cauchy sequence) if, for every ε > 0, there is an integer M such that any two sequence elements that are both beyond M are within ε of each other.
converges in the sense of Cauchy (or is a Cauchy sequence) if, for every ε > 0, there is an integer M such that any two sequence elements that are both beyond M are within ε of each other.
- Whenever
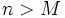 and
and 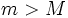 ,
, 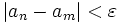 .
.
- Whenever
Note that there is no reference to the mysterious number A—the convergence is defined purely in terms of the sequence elements being close to each other. The example sequence given above can be shown to be a Cauchy sequence.
Construction of the Real Numbers[edit]
What we did above effectively defined 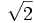 in terms of the rationals, by saying
in terms of the rationals, by saying
- "The square root of 2 is whatever the Cauchy sequence given above converges to."
even though that isn't a "number" according to our limited (rationals-only) understanding of what a number is.
The real numbers can be defined this way, by saying that a real number is defined to be a Cauchy sequence of rational numbers.
There are many details that we won't work out here; among them are:
- There are different Cauchy sequences that converge to the same thing; we gave two sequences above that converged to
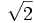 . So a real number is actually an "equivalence class" of Cauchy sequences, under a carefully defined equivalence. This is a bit tricky.
. So a real number is actually an "equivalence class" of Cauchy sequences, under a carefully defined equivalence. This is a bit tricky. - We have to show how to add, subtract, multiply, and divide Cauchy sequences. This is a bit tricky.
- We have to give the Cauchy sequences corresponding to rational numbers. This is easy—5/12 becomes (5/12, 5/12, 5/12, ...).
Once we have done that, the payoff is enormous. We have defined an extension to the rationals that is metrically complete—that extension of the rationals is the real numbers. Metrically complete means that every Cauchy sequence made from the set converges to an element which is itself in the set. The reals are the metric completion of the rationals.
The use of Cauchy sequences is one of the two famous ways of defining the real numbers, that is, completing the rationals. The other method is Dedekind cuts
External links[edit]
- "Cauchy Sequence" From MathWorld
- "Completion" From MathWorld
Categories: [Mathematics] [Calculus]
↧ Download as ZWI file | Last modified: 02/16/2023 21:06:44 | 3 views
☰ Source: https://www.conservapedia.com/Cauchy_sequence | License: CC BY-SA 3.0
 ZWI signed:
ZWI signed:
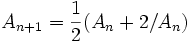
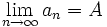
 KSF
KSF