Heptagrammic-Order Heptagonal Tiling
From Handwiki In geometry, the heptagrammic-order heptagonal tiling is a regular star-tiling of the hyperbolic plane. It has Schläfli symbol of {7,7/2}. The vertex figure heptagrams are {7/2}, 
. The heptagonal faces overlap with density 3.
Related tilings
It has the same vertex arrangement as the regular order-7 triangular tiling, {3,7}. The full set of edges coincide with the edges of a heptakis heptagonal tiling.
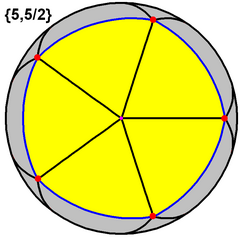
It is related to a Kepler-Poinsot polyhedron, the great dodecahedron, {5,5/2}, which is polyhedron and a density-3 regular star-tiling on the sphere (resembling a regular icosahedron in this state, similarly to this tessellation resembling the order-7 triangular tiling):
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN:978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8.
External links
- Weisstein, Eric W.. "Hyperbolic tiling". http://mathworld.wolfram.com/HyperbolicTiling.html.
- Weisstein, Eric W.. "Poincaré hyperbolic disk". http://mathworld.wolfram.com/PoincareHyperbolicDisk.html.
Tessellation | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|   | ||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
 |  |
Categories: [Heptagonal tilings] [Hyperbolic tilings] [Isogonal tilings] [Isohedral tilings] [Regular tilings]
↧ Download as ZWI file | Last modified: 06/24/2023 17:36:12 | 2 views
☰ Source: https://handwiki.org/wiki/Heptagrammic-order_heptagonal_tiling | License: CC BY-SA 3.0
ZWI signed:
KSF