Clock
 From Britannica 11th Edition (1911)
From Britannica 11th Edition (1911) Clock. The measurement of time has always been based on the revolution of the celestial bodies, and the period of the apparent revolution of the sun, i.e. the interval between two consecutive crossings of a meridian, has been the usual standard for a day. By the Egyptians the day was divided into 24 hours of equal length. The Greeks adopted a different system, dividing the day, i.e. the period from sunrise to sunset, into 12 hours, and also the night. Whence it followed that it was only at two periods in the year that the length of the hours during the day and night were uniform (see Calendar). In consequence, those who adopted the Greek system were obliged to furnish their water-clocks (see Clepsydra) with a compensating device so that the equal hours measured by those clocks should be rendered unequal, according to the exigencies of the season. The hours were divided into minutes and seconds, a system derived from the sexagesimal notation which prevailed before the decimal system was finally adopted. Our mode of computing time, and our angular measure, are the only relics of this obsolete system.
The simplest measure of time is the revolution of the earth round its axis, which so far as we know is uniform, perfectly regular, and has not varied in speed during any period of human observation. The time of such a revolution is called a sidereal day, and is divided into hours, minutes and seconds. The period of rotation of the earth is practically measured by observations of the fixed stars (see Time), the period between two successive transits of the same star across a meridian constituting the sidereal day. But as the axis of the earth slowly revolves round in a cone, whereby the phenomenon known as the precession of the equinoxes is produced, it follows that the astronomical sidereal day is not the true period of the earth’s rotation on its axis, but varies from it by less than a twenty millionth part, a fraction so small as to be inappreciable. But the civil day depends not on the revolution of the earth with regard to the stars, but on its revolution as compared with the position of the sun. Therefore each civil day is on the average longer than a sidereal one by nearly four minutes, or, to be exact, each sidereal day is to an average civil day as .99727 to 1, and the sidereal hour, minute and second are also shorter in like proportion. Hence a sidereal clock has a shorter, quicker-moving pendulum than an ordinary clock.
Ordinary civil time thus depends on the apparent revolution of the sun round the earth. As, however, this is not uniform, it is needful for practical convenience to give it an artificial uniformity. For this purpose an imaginary sun, moving round the earth with the average velocity of the real sun, and called the “mean” sun, is taken as the measure of civil time. The day is divided into 24 hours, each hour into 60 minutes, and each minute into 60 seconds. After that the sexagesimal division system is abandoned, and fractions of seconds are estimated in decimals.
A clock consists of a train of wheels, actuated by a spring or weight, and provided with a governing device which so regulates the speed as to render it uniform. It also has a mechanism by which it strikes the hours on a bell or gong (cp. Fr. cloche, Ger. Glocke, a bell; Dutch klok, bell, clock), whereas, strictly, a timepiece does not strike, but simply shows the time.
The earliest clocks seem to have come into use in Europe during the 13th century. For although there is evidence that they may have been invented some centuries sooner, yet until that date they were probably only curiosities. The first form they took was that of the balance clock, the invention of which is ascribed, but on very insufficient grounds, to Pope Silvester II. in A.D. 996. A clock was put up in a former clock tower at Westminster with some great bells in 1288, out of a fine imposed on a chief-justice who had offended the government, and the motto Discite justitiam, moniti, inscribed upon it. The bells were sold, or rather, it is said, gambled away, by Henry VIII. In 1292 a clock in Canterbury cathedral is mentioned as costing £30, and another at St Albans, by R. Wallingford, the abbot in 1326, is said to have been such as there was not in all Europe, showing various astronomical phenomena. A description of one in Dover Castle with the date 1348 on it was published by Admiral W.H. Smyth (1788-1865) in 1851, and the clock itself was exhibited going, in the Scientific Exhibition of 1876. A very similar one, made by Henry de Vick for the French king Charles V. in 1379 was much like the common clocks of the 18th century, except that it had a vibrating balance instead of a pendulum. The works of one of these old clocks still exist in a going condition at the Victoria and Albert Museum. It came from Wells cathedral, having previously been at Glastonbury abbey.
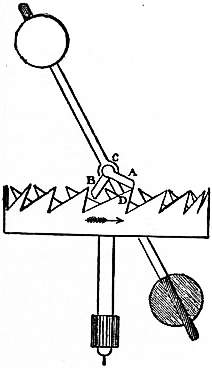 |
| Fig. 1.—Verge Escapement. |
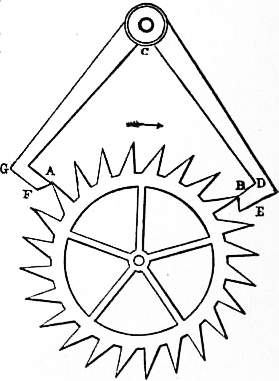
These old clocks had what is called a verge escapement, and a balance. The train of wheels ended with a crown wheel, that is, a wheel serrated with teeth like those of a saw, placed parallel with its axis (fig. 1). These teeth, D, engaged with pallets CB, CA, mounted on a verge or staff placed parallel to the face of the crown wheel. As the crown wheel was turned round the teeth pushed the pallets alternately until one or the other slid past a tooth, and thus let the crown wheel rotate. When one pallet had slipped over a tooth, the other pallet caught a corresponding tooth on the opposite side of the wheel. The verge was terminated by a balance rod placed at right angles to it with a ball at each end. It is evident that when the force of any tooth on the crown wheel began to act on a pallet, it communicated motion to the balance and thus caused it to rotate. This motion would of course be accelerated, not uniformly, but according to some law dependent on the shape of the teeth and pallets. When the motion had reached its maximum, the tooth slipped past the pallet. The other pallet now engaged another tooth on the opposite side of the wheel. The motion of the balls, however, went on and they continued to swing round, but this time they were opposed by the pressure of the tooth. For a time they overcame that pressure, and drove the tooth back, causing a recoil. As, however, every motion if subjected to an adverse acceleration (i.e. a retardation) must come to rest, the balls stopped, and then the tooth, which had been forced to recoil, advanced in its turn, and the swing was repeated. The arrangement was thus very like a huge watch balance wheel in which the driving weight acted in a very irregular manner, not only as a driving force, but also as a regulating spring. The going of such clocks was influenced greatly by friction and by the oil on the parts, and never could be satisfactory, for the time varied with every variation in the swing of the balls, and this again with every variation of the effective driving force.
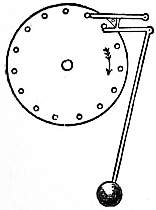 |
| Fig. 2.—Galileo’s Escapement. |
The first great step in the improvement of the balance clock was a very simple one. In the 17th century Galileo had discovered the isochronism of the pendulum, but he made no practical use of it, except by the invention of a little instrument for enabling doctors to count their patients’ pulse-beats. His son, however, is supposed to have applied the pendulum to clocks. There is at the Victoria and Albert Museum a copy of an early clock, said to be Galileo’s, in which the pins on a rotating wheel kick a pendulum outwards, remaining locked after having done so till the pendulum returns and unlocks the next pin, which then administers another kick to the pendulum (fig. 2). The interest of the specimen is that it contains the germ of the chronometer escapement and free pendulum, which is possibly destined to be the escapement of the future.
The essential component parts of a clock are:—
1. The pendulum or time-governing device;
2. The escapement, whereby the pendulum controls the speed of going;
3. The train of wheels, urged round by the weight or main-spring, together with the recording parts, i.e. the dial, hands and hour motion wheels;
4. The striking mechanism.
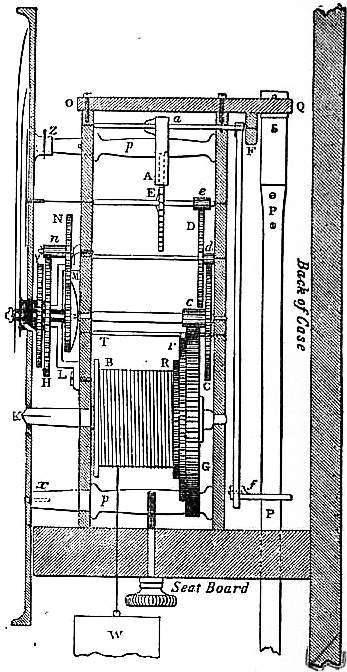 |
| Fig. 3.—Section of House Clock. |
The general construction of the going part of all clocks, except large or turret clocks, is substantially the same, and fig. 3 is a section of any ordinary house clock. B is the barrel with the cord coiled round it, generally 16 times for the 8 days; the barrel is fixed to its arbor K, which is prolonged into the winding square coming up to the face or dial of the clock; the dial is here shown as fixed either by small screws x, or by a socket and pin z, to the prolonged pillars p, p, which (4 or 5 in number) connect the plates or frame of the clock together, though the dial is commonly set on to the front plate by another set of pillars of its own. The great wheel G rides on the arbor, and is connected with the barrel by the ratchet R, the action of which is shown more fully in fig. 25. The intermediate wheel r in this drawing is for a purpose which will be described hereafter, and for the present it may be considered as omitted, and the click of the ratchet R as fixed to the great wheel. The great wheel drives the pinion c which is called the centre pinion, on the arbor of the centre wheel C, which goes through to the dial, and carries the long, or minute-hand; this wheel always turns in an hour, and the great wheel generally in 12 hours, by having 12 times as many teeth as the centre pinion. The centre wheel drives the “second wheel” D by its pinion d, and that again drives the scape-wheel E by its pinion e. If the pinions d and e have each 8 teeth or leaves (as the teeth of pinions are usually called), C will have 64 teeth and D 60, in a clock of which the scape-wheel turns in a minute, so that the seconds hand may be set on its arbor prolonged to the dial. A represents the pallets of the escapement, which will be described presently, and their arbor a goes through a large hole in the back plate near F, and its back pivot turns in a cock OFQ screwed on to the back plate. From the pallet arbor at F descends the crutch Ff, ending in the fork f, which embraces the pendulum P, so that as the pendulum vibrates, the crutch and the pallets necessarily vibrate with it. The pendulum is hung by a thin spring S from the cock Q, so that the bending point of the spring may be just opposite the end of the pallet arbor, and the edge of the spring as close to the end of that arbor as possible.
We may now go to the front (or left hand) of the clock, and describe the dial or “motion-work.” The minute hand fits on to a squared end of a brass socket, which is fixed to the wheel M, and fits close, but not tight, on the prolonged arbor of the centre wheel. Behind this wheel is a bent spring which is (or ought to be) set on the same arbor with a square hole (not a round one as it sometimes is) in the middle, so that it must turn with the arbor; the wheel is pressed up against this spring, and kept there, by a cap and a small pin through the end of the arbor. The consequence is, that there is friction enough between the spring and the wheel to carry the hand round, but not enough to resist a moderate push with the finger for the purpose of altering the time indicated. This wheel M, which is sometimes called the minute-wheel, but is better called the hour-wheel as it turns in an hour, drives another wheel N, of the same number of teeth, which has a pinion attached to it; and that pinion drives the twelve-hour wheel H, which is also attached to a large socket or pipe carrying the hour hand, and riding on the former socket, or rather (in order to relieve the centre arbor of that extra weight) on an intermediate socket fixed to the bridge L, which is screwed to the front plate over the hour-wheel M. The weight W, which drives the train and gives the impulse to the pendulum through the escapement, is generally hung by a catgut line passing through a pulley attached to the weight, the other end of the cord being tied to some convenient place in the clock frame or seat-board, to which it is fixed by screws through the lower pillars.
 |
| Fig. 4. |
Pendulum.—Suppose that we have a body P (fig. 4) at rest, and that it is material, that is to say, has “mass.” And for simplicity let us consider it a ball of some heavy matter. Let it be free to move horizontally, but attached to a fixed point A by means of a spring. As it can only move horizontally and not fall, the earth’s gravity will be unable to impart any motion to it. Now it is a law first discovered by Robert Hooke (1635-1703) that if any elastic spring be pulled by a force, then, within its elastic limits, the amount by which it will be extended is proportional to the force. Hence then, if a body is pulled out against a spring, the restitutional force is proportional to the displacement. If the body be released it will tend to move back to its initial position with an acceleration proportioned to its mass and to its distance from rest. A body thus circumstanced moves with harmonic motion, vibrating like a stretched piano string, and the peculiarity of its motion is that it is isochronous. That is to say, the time of returning to its initial position is the same, whether it makes a large movement at a high velocity under a strong restitutional force, or a small movement at a lower velocity under a smaller restitutional force (see Mechanics). In consequence of this fact the balance wheel of a watch is isochronous or nearly so, notwithstanding variations in the amplitude of its vibrations. It is like a piano string which sounds the same note, although the sound dies away as the amplitude of its vibrations diminishes.
 |
| Fig. 5. |
A pendulum is isochronous for similar reasons. If the bob be drawn aside from D to C (fig. 5), then the restitutional force tending to bring it back to rest is approximately the force which gravitation would exert along the tangent CA, i.e.
| g cos ACW = g | BC | = g | displacement BC | . |
| OC | length of pendulum |
Since g is constant, and the length of the pendulum does not vary, it follows that when a pendulum is drawn aside through a small arc the force tending to bring it back to rest is proportional to the displacement (approximately). Thus the pendulum bob under the influence of gravity, if the arc of swing is small, acts as though instead of being acted on by gravity it was acted on by a spring tending to drag it towards D, and therefore is isochronous. The qualification “If the arc of swing is small” is introduced because, as was discovered by Christiaan Huygens, the arc of vibration of a truly isochronous pendulum should not be a circle with centre O, but a cycloid DM, generated by the rolling of a circle with diameter DQ = ½OD, upon a straight line QM. However, for a short distance near the bottom, the circle so nearly coincides with the cycloid that a pendulum swinging in the usual circular path is, for small arcs, isochronous for practical purposes.
 |
| Fig. 6. |
The formula representing the time of oscillation of a pendulum, in a circular arc, is thus found:—Let OB (fig. 6) be the pendulum, B be the position from which the bob is let go, and P be its position at some period during its swing. Put FC = h, and MC = x, and OB = l. Now when a body is allowed to move under the force of gravity in any path from a height h, the velocity it attains is the same as a body would attain falling freely vertically through the distance h. Whence if v be the velocity of the bob at P, v = √2gFM = √2g(h - x). Let Pp = ds, and the vertical distance of p below P = dx, then Pp = velocity at P × dt; that is, dt = ds/v. Also
| ds | = | 1 | = | 1 | , |
| dx | MP | √x(2l - x) |
whence
| dt = | ds | = | ldx | . | 1 | = | 1 | √ | l | . | dx | . | 1 | . |
| v | √x(2l - x) | √2g(h - x) | 2 | g | √x(p - x) | √1 - (x/2l) |
Expanding the second part we have
| dt = | 1 | √ | l | . | dx | . ( 1 + | x | + ... ) . |
| 2 | g | √x(h - x) | 4l |
If this is integrated between the limits of 0 and h, we have
| t = π √ | l | . ( 1 + | h | + ... ) , |
| g | 8l |
where t is the time of swing from B to A. The terms after the second may be neglected. The first term, π √l/g, is the time of swing in a cycloid. The second part represents the addition necessary if the swing is circular and not cycloidal, and therefore expresses the “circular error.” Now h = BC²/l = 2π²θ²l/360², where θ is half the angle of swing expressed in degrees; hence h/8l = θ²/52520, and the formula becomes
| t = π √ | l | ( 1 + | θ² | ) . |
| g | 52520 |
Hence the ratio of the time of swing of an ordinary pendulum of any length, with a semiarc of swing = θ degrees is to the time of swing of a corresponding cycloidal pendulum as 1 + θ²/52520 : 1. Also the difference of time of swing caused by a small increase θ′ in the semiarc of swing = 2θθ′ / 52520 second per second, or 3.3θθ′ seconds per day. Hence in the case of a seconds pendulum whose semiarc of swing is 2° an increase of .1° in this semiarc of 2° would cause the clock to lose 3.3 × 2 × 0.1 = .66 second a day.
Huygens proposed to apply his discovery to clocks, and since the evolute of a cycloid is an equal cycloid, he suggested the use of a flexible pendulum swinging between cycloidal cheeks. But this was only an example of theory pushed too far, because the friction on the cycloidal cheeks involves more error than they correct, and other disturbances of a higher degree of importance are left uncorrected. In fact the application of pendulums to clocks, though governed in the abstract by theory, has to be modified by experiment.
Neglecting the circular error, if L be the length of a pendulum and g the acceleration of gravity at the place where the pendulum is, then T, the time of a single vibration = π√(L/g). From this formula it follows that the times of vibration of pendulums are directly proportional to the square root of their lengths, and inversely proportional to the square root of the acceleration of gravity at the place where the pendulum is swinging. The value of g for London is 32.2 ft. per second per second, whence it results that the length of a pendulum for London to beat seconds of mean solar time = 39.14 in. nearly, the length of an astronomical pendulum to beat seconds of sidereal time being 38.87 in.
This length is calculated on the supposition that the arc of swing is cycloidal and that the whole mass of the pendulum is concentrated at a point whose distance, called the radius of oscillation, from the point of suspension of the pendulum is 39.14 in. From this it might be imagined that if a sphere, say of iron, were suspended from a light rod, so that its centre were 39.14 in. below its point of support, it would vibrate once per second. This, however, is not the case. For as the pendulum swings, the ball also tends to turn in space to and fro round a horizontal axis perpendicular to the direction of its motion. Hence the force stored up in the pendulum is expended, not only in making it swing, but also in causing the ball to oscillate to and fro through a small angle about a horizontal axis. We have therefore to consider not merely the vibrations of the rod, but the oscillations of the bob. The moment of the momentum of the system round the point of suspension, called its moment of inertia, is composed of the sum of the mass of each particle multiplied into the square of its distance from the axis of rotation. Hence the moment of inertia of the body I = Σ(ma²). If k be defined by the relation Σ(ma²) = Σ(m) X k², then k is called the radius of gyration. If k be the radius of gyration of a bob round a horizontal axis through its centre of gravity, h the distance of its centre of gravity below its point of suspension, and k’ the radius of gyration of the bob round the centre of suspension, then k′² = h² + k². If l be the length of a simple pendulum that oscillates in the same time, then lh = k′² = h² + k². Now k can be calculated if we know the form of the bob, and l is the length of the simple pendulum = 39.14 in.; hence h, the distance of the centre of gravity of the bob below the point of suspension, can be found.
In an ordinary pendulum, with a thin rod and a bob, this distance h is not very different from the theoretical length, l = 39.14 in., of a simple theoretical pendulum in which the rod has no weight and the bob is only a single heavy point. For the effect of the weight of the rod is to throw the centre of oscillation a little above the centre of gravity of the bob, while the effect of the size of the bob is to throw the centre of oscillation a little down. In ordinary practice it is usual to make the pendulum so that the centre of gravity is about 39 in. below the upper free end of the suspension spring and leave the exact length to be determined by trial.
 |
| Fig. 7.—Section of Westminster Clock Pendulum. |
Since T = π√L/g, we have, by differentiating, dL/L = 2dT/T, that is, any small percentage of increase in L will correspond to double the percentage of increase in T. Therefore with a seconds pendulum, in order to make a second’s difference in a day, equivalent to 1/86,400 of the pendulum’s Regulation. rate of vibration, since there are 86,400 seconds in 24 hours, we must have a difference of length amounting to 2/86,400 = 1/43,200 of the length of the rod. This is 39.138/43,200 = .000906 in. Hence if under the pendulum bob be put a nut working a screw of 32 threads to the inch and having its head divided into 30 parts, a turn of this nut through one division will alter the length of the pendulum by .0009 in. and change the rate of the clock by about a second a day. To accelerate the clock the nut has always to be turned to the right, or as you would drive in a corkscrew and vice versa. But in astronomical and in large turret clocks, it is desirable to avoid stopping or in any way disturbing the pendulum; and for the finer adjustments other methods of regulation are adopted. The best is that of fixing a collar, as shown in fig. 7 at C, about midway down the rod, capable of having very small weights laid upon it, this being the place where the addition of any small weight produces the greatest effect, and where, it may be added, any moving of that weight up or down on the rod produces the least effect. If M is the weight of the pendulum and l its length (down to the centre of oscillation), and m a small weight added at the distance n below the centre of suspension or above the c.o. (since they are reciprocal), t the time of vibration, and -dt the acceleration due to adding m; then
| -dt | = | m | ( | n | - | n² | ) ; |
| t | 2M | l | l² |
from which it is evident that if n = l/2, then = dt/t = m/8M. But as there are 86400 seconds in a day, -dT, the daily acceleration, = 86400 dt, or 10800 m/M, or if m is the 10800th of the weight of the pendulum it will accelerate the clock a second a day, or 10 grains will do that on a pendulum of 15 ℔ weight (7000 gr. being = 1 ℔.), or an ounce on a pendulum of 6 cwt. In like manner if n = l/3 from either top or bottom, m must = M/7200 to accelerate the clock a second a day. The higher up the collar the less is the risk of disturbing the pendulum in putting on or taking off the regulating weights, but the bigger the weight required to produce the effect. The weights should be made in a series, and marked ¼, ½, 1, 2, according to the number of seconds a day by which they will accelerate; and the pendulum adjusted at first to lose a little, perhaps a second a day, when there are no weights on the collar, so that it may always have some weight on, which can be diminished or increased from time to time with certainty, as the rate may vary.
The length of pendulum rods is also affected by temperature and also, if they are made of wood, by damp. Hence, to ensure good time-keeping qualities in a clock, it is necessary (1) to make the rods of materials that are as little affected by such Compensation. influences as possible, and (2) to provide means of compensation by which the effective length of the rod is kept constant in spite of expansion or contraction in the material of which it is composed. Fairly good pendulums for ordinary use may be made out of very well dried wood, soaked in a thin solution of shellac in spirits of wine, or in melted paraffin wax; but wood shrinks in so uncertain a manner that such pendulums are not admissible for clocks of high exactitude. Steel is an excellent material for pendulum rods, for the metal is strong, is not stretched by the weight of the bob, and does not suffer great changes in molecular structure in the course of time. But a steel rod expands on the average lineally by .0000064 of its length for each degree F. by which its temperature rises; hence an expansion of .00009 in. on a pendulum rod of 39.14 in., that is .000023 of its length, will be caused by an increase of temperature of about 4° F., and that is sufficient to make the clock lose a second a day. Since the summer and winter temperatures of a room may differ by as much as 50° F., the going of a clock may thus be affected by an error of 12 seconds a day. With a pendulum rod of brass, which has a coefficient of expansion of .00001, a clock might gain one-third of a minute daily in winter as compared with its rate in summer. The coefficients of linear expansion per degree F. of some other materials used in making pendulums are as follows: white deal, .0000024; flint glass, .0000048; iron, .000007; lead, .000016; zinc, .000016; and mercury, .000033. The solid or cubical expansions of these bodies are three times the above quantities respectively.
The first method of compensating a pendulum was invented in 1722 by George Graham, who proposed to use a bob of mercury, taking advantage of the high coefficient of expansion of that metal. As now employed, the mercurial pendulum consists of a rod of steel terminating in a stirrup of the same metal on which rests a glass vessel full of mercury, having its centre of gravity about 39 in. below the point of suspension of the pendulum. For each Fahrenheit degree of temperature the centre of gravity of the bob is lowered by the expansion of the rod about 1⁄4000 of an inch. The glass vessel and the mercury in it have therefore to be so contrived, that their centre of gravity will rise 1⁄4000 in. per degree F. The glass having a small coefficient of expansion, the lateral expansion of the mercury will be checked by it, and this will help to raise the column. For the linear coefficient of expansion of glass is .0000048 per degree F., whence the sectional area of a glass vessel increases by .0000096 per degree F., and therefore the coefficient of vertical expansion of a column of mercury whose volumetric expansion coefficient is .0001 per degree F. is (.0001 - .0000096) = .0000904. Let x be the height of the vessel necessary to compensate a steel rod upon the bottom of which it rests. Then, the coefficient of expansion of steel being .0000066 per degree F., we have
| x | (.0000904 - .0000066) = .0000066 × 39.14, whence x = 6¼ in. |
| 2 |
It must, however, be remembered that the glass jar has some weight and that it does not rise by anything like the amount of the mercury. This tends to keep the centre of gravity down. So that the height of mercury of 6¼ in. will not be sufficient to effect the compensation, and about 6¾ to 7 in. will be required. Some authors specify 7 in.; this is when the diameter of the jar is small. A certain amount of negative compensation must also be deducted to allow for the changes of temperature in the air, as will presently be seen; this amounts in the case of mercury to about 1⁄5 in.
In consequence of the complication of all these calculations it is usual to allow about 6¾ to 7 in. of mercury in the glass vessel and to adjust the exact amount of mercury by trial.
Another very good form of mercurial pendulum was proposed by E. J. Dent; it consists of a cast-iron jar into the top of which the steel pendulum rod is screwed, having its end plunged into the mercury contained in the jar. By this means the mercury, jar and rod rapidly acquire the same temperature. This pendulum is less likely to break than the form just described. The depth of mercury required in an iron jar is stated by Lord Grimthorpe to be 8½ to 9 in. The reason why it is greater than it is when a glass jar is employed is that iron has a larger coefficient of expansion than glass, and that it is also heavier. In all cases, however, of mercury pendulums experiment seems to be the only ultimate test of the quantity of mercury required, for the results are so complicated by the behaviour of the oil and the barometric errors that at its best the regulation of a clock can only be ultimately a matter of scientifically guided compromise. A small amount of compensation of a purely experimental character is also allowed to compensate the changes which temperature effects on the suspension spring. This is sometimes made as much as 1⁄6 of the length correction.
As an alternative to the mercurial pendulum other systems have been employed. The “gridiron” pendulum consists of a group of alternate rods of steel and brass, so arranged that the expansion of the brass acts upwards and counteracts that of the steel downwards. It was invented in 1726 by John Harrison. Assuming that 9 rods are used—5 of steel and 4 of brass—their lengths may be as follows from pin to pin:—Centre steel rod 31.5 in.; 2 steel rods next the centre 24.5 in.; 2 steel rods farthest from centre 29.5 in.; from the lower end of outside steel rods to centre of bob 3 in.; total 89.5 in. Of the 4 brass rods the 2 outside ones are 26.87 in.; and the two inside ones 22.25 in.; total 49.12 in. Thus the expansion of 88½ in. of steel is counteracted by the expansion of 491⁄8 in. of brass. Everything depends, however, on the expansion coefficient of the steel and brass employed, the requirement in every case being that of total lengths of the brass and iron should be in proportion to the linear coefficients of expansion of those metals. The above figures are for a very soft brass and steel. Thos. Reid, with more ordinary steel and brass, prescribed a ratio of 112 to 71, Lord Grimthorpe a ratio of 100 to 61. It is absolutely necessary to put the actual rods to be used for making the pendulum in a hot water bath, and measure their expansions with a microscope.
John Smeaton, taking advantage of a far greater expansion coefficient of zinc as compared with brass, proposed to use a steel rod with a collar at the bottom, on which rested a hard drawn zinc rod. From this rod hung a steel tube to which the bob was attached. The total length of the steel rod and of the steel tube down to the centre of the bob was made to the total length of the zinc tube, in the ratio of 5 to 2 (being the ratio of the expansions of zinc and steel); for a 39.14 in. pendulum we should therefore want a zinc tube equal in length to 2⁄3 (39.14) = 26¼ in. In practice the zinc tube is made about 27 in. long, and then gradually cut down by trial. In fact the weight of a heavy pendulum squeezes the zinc, and it is impossible by mere theory to determine what will be its behaviour. The zinc tube must be of rolled zinc, hard drawn through a die, and must not be cast. Ventilating holes must be made in suitable places in the steel tube and the collar on which it rests, to ensure that changes of temperature are rapidly communicated throughout the system.
A pendulum with a rod of dry varnished deal is tolerably compensated by a bob of lead or of zinc 10½ to 13 in. in height, resting on a nut at the bottom of the rod.
The old methods of pendulum compensation for heat may now be considered as superseded by the invention of “invar,” a combination of nickel and steel, due to Charles E. Guillaume, of the International Office of Weights and Measures at Invar. Sèvres near Paris. This alloy has a linear coefficient of expansion on the average of .000001 per degree centigrade, that is to say, only about 1⁄11 that of ordinary steel. Hence it can be easily compensated by means of brass, lead or any other suitable metal. Brass is usually employed. In the invar pendulum introduced into Great Britain by Mr Agar Baugh a departure is made from the previous practice of merely calculating the length of the compensator, fastening it to the lower part of the pendulum, and attaching it to the centre of the bob. In the case of these pendulums, accurate computations are made of the moments of inertia of every separate individual part. Thus, for instance, since an addition of volume due to the effect of heat to the upper part of the bob has a different effect upon the moment of inertia from that of an equal quantity added to the lower part of the bob, the bob is suspended not from its centre, but from a point about 1⁄10 in. below it, the distance varying according to the shape of the bob, so that the heat expansion of the bob may cause its centre of gravity to rise and compensate the effect of its increased moment of inertia. Again the suspension spring is measured for isochronism, and an alloy of steel prepared for it which does not alter its elasticity with change of temperature. Moreover, since rods of invar steel subjected to strain do not acquire their final coefficients of expansion and elasticity for some time, the invar is artificially “aged” by exposure to strain and heat.
These considerations serve as a guide in arranging for the compensation of the expansion of the rod and bob due to change of temperature. But they are not the only ones required; we have also to deal with changes due to the density of the air in which the pendulum is moving. A body suspended in a fluid loses in weight by an amount equal to the weight of the fluid displaced, whence it follows that a pendulum suspended in air has not the weight which ought truly to correspond to its mass. M remains constant while Mg is less than in a vacuum. If the density of the air remained constant, this loss of weight, being constant, could be allowed for and would make no difference to the time-keeping. The period of swing would only be a little increased over what it would be in vacuo. But the weight of a given volume of air varies both with the barometric pressure and also with temperature. If the bob be of type metal it weighs less in air than in a vacuum by about .000103 part, and for each 1° F. rise in temperature (the barometer remaining constant and therefore the pressure remaining the same), the variation of density causes the bob to gain .00000024 of its weight. This, of course, makes the pendulum go quicker. Since the time of vibration varies as the inverse square root of g, it follows that a small increment of weight, the mass remaining constant, produces a diminution of one half that increment in time of swing. Hence, then, a rise of temperature of 1° F. will produce a diminution in the time of swing of .00000012th part or .0104 second in a day. But in making this calculation it has been assumed that the mass moved remains unaltered by the temperature. This is not so. A pendulum when swinging sets in motion a volume of air dependent on the size of the bob, but in a 10 ℔ bob nearly equal to its own volume. Hence while the rise of 1° of temperature increases the weight by .00000012th part, it also decreases the mass by about the same proportion, and therefore the increase of period due to a rise of temperature of 1° F. will, instead of being .0104 second a day, be about .02 second. This must be compensated negatively by lengthening the pendulum by about .02⁄1000 in. for each degree of rise of temperature, which will require a piece of brass about 2 in. long. It follows, therefore, that with an invar rod having a linear expansion coefficient of .0000002 per degree F., which requires a piece of brass about .8 in. long to compensate it, the compensation which is to regulate both the expansion of the rod and also that of the air must be .8 in. - 2 in., or -1.2 in.; so that the bob must be hung downwards from a piece of brass nearly 11⁄5 in. in length. If the coefficient of expansion of the invar were .00000053 per degree F., then the two corrections, one for the expansion of the rod and the other for the expansion of the air, would just neutralize one another, and the pendulum rod would require no compensator at all. There are a number of other refinements which might be added, but which are too long for insertion here. By taking in all the sources of error of higher orders, it has been possible to calculate a pendulum so accurately that, when the clock is loaded with the weight sufficient to give the pendulum the arc of swing for which it is designed, a rate of error has been produced of only half a minute in a year. These refinements, however, are only required for clocks of precision; for ordinary clocks an invar pendulum with a lead bob and brass compensator is quite sufficient.
Invar pendulum rods are often made of steel with coefficients of expansion of about .0000012 linear per 1° C.; such a bob as this would require about 6.7 cm. of brass to compensate it, and, deducting 5 cm. of brass for the air compensation, this leaves about 1.7 cm. of positive compensation for the pendulum. But as has been said, the exact deduction depends on the shape and size of the bob, and the metal of which it is made. The diameters of the rods are 8 mm. for a 15 ℔ bob, 5 mm. for a 4 ℔ bob, and 12 to 15 mm. for a 60 ℔ bob. The bob is either a single cylinder or two cylinders with the rod between them. Lenticular and spherical bobs are not used. The great object is to allow the air ready access to all parts of the rod and compensator, so that they are all heated or cooled simultaneously. The bobs are usually made of a compound of lead, antimony, and tin, which forms a hard metal, free from bubbles and with a specific gravity of about 10. The usual weight of the bobs of the best pendulums for an ordinary astronomical clock is about 15 ℔. A greater weight than this is found liable to make the support of the pendulum rock and to put an undue strain on the parts, without any corresponding advantage. The rods used are all artificially aged, and have their heat expansion measured. No adjusting screw at the bottom is provided, the regulation being done by the addition of weights half way up the rod. An adjusting screw at the bottom has the disadvantage that it is impossible to know on which of the threads the rod is really resting; hence extra compensation may be introduced when not required. It is considered better that the supports of the bob should be rigid and invariable.
The effect of changes in the pressure of the air as shown by a barometer is too important to be omitted in the design of a good clock. But we do not propose to give more than a mere indication of the principles which govern compensation Barometrical error. for this effect, since the full discussion of the problem would be too protracted. We have seen that the action of the air in affecting the time of oscillation of a pendulum depends chiefly on the fact that its buoyancy makes the pendulum lighter, so that while the mass of the bob which has to be moved remains the same or nearly the same, the acceleration of gravity on it has less effect. A volume of air at ordinary temperature and pressure has, as has been said, .000103 the weight of an equal volume of type metal, whence it follows that the acceleration of gravity on a type metal bob in air is .999897 of the acceleration of gravity on the bob in vacuo. If, therefore, we diminish the value of g in the formula T = π√L/g by .000103, we shall have the difference of time of vibration of a type metal bob in air, as compared with its time in vacuo, and this, by virtue of the principle used when discussing the increase of time of oscillation due to increased pendulum lengths, is ½(.000103) second in one second, or about 4½ seconds in a day of 86,400 seconds. It follows that a barometric pressure of 30 in. causes a loss of 4½ seconds in the day, equivalent to .15 second per day for each inch of difference of the barometer. But, as has already been explained, the effect of the mass of the air transported with the pendulum must also be taken into account and therefore the above figures must be doubled or nearly doubled. A difference of 30 in. of barometric pressure would thus make a difference of 9 seconds per day in the rate of the pendulum, and the clock would lose about 1⁄3 of a second a day for each inch of rise of the barometer, the result being of the same magnitude as would be produced by a fall of temperature of 15° F. in the air. Either of these effects would require a shortening of the pendulum of 1⁄3000 in. This estimate is not far from the truth, for observations taken at various European observatories on various clocks, and collected by Jakob Hilfiker, give a mean of .15 second of retardation per day per centimetre of barometric pressure, or .37 second per day for each inch rise of the barometer.
In order to counteract variations in going which must thus obviously be produced by variations of barometrical pressure, attempts have been made purposely to disturb the isochronism of the pendulum, by making the arcs of vibration abnormally large. Again, the bob has been fitted with a piece of iron, which is subjected to the attraction of a piece of magnetized steel floating on the mercury in the open end of a barometer tube, so that when the barometer falls the attraction is increased and the pendulum retarded. Again, mercury barometers have been attached to pendulums. A simple method is to fix an aneroid barometer with about seven compartments on the pendulum about 5 to 6 in. below the suspension spring, and to attach to the top of it a suitable weight which is lowered as the barometric pressure increases. One of the best methods of neutralizing the effects of variations of barometric pressure is to enclose the whole clock in an air-tight case, which may either be a large glass cylinder or a square case with a stout plate-glass front. This renders it independent of outside variations, whether of temperature or pressure, and keeps the density of the air inside the case uniform. If the case could be completely, or almost completely, exhausted of air, and kept so exhausted, of course the pendulum would experience the minimum of resistance and would have to be lengthened a little. But in practice it is impossible to secure the maintenance of a good vacuum without sealing up the case in such a way as to render repairs very difficult, and this plan is therefore rarely resorted to. What is usually done is to put the clock in a metal case covered with a thick sheet of plate glass bedded in india-rubber strips, and held down by an iron flanged lid or frame firmly fixed by means of small bolts. An air-pump is attached to the case, a turn-off tap being inserted, and by a few strokes the pressure of the air inside the case can be lowered to (say) 29 in., or a little below the usual barometric height at the place where the clock is. The difference of pressure being small, the tendency of air from outside to leak in is also small, and if the workmanship is good the inside pressure will remain unaltered for many days. In any case the difference produced by leakage will be small, and will not greatly affect the going of the clock. With care, and a daily or weekly touch of the pump, the pressure inside can be kept practically constant, and hence the atmospheric error will be eliminated. The cover has also incidentally the effect of keeping damp and fumes from the clock and thus preserving it from rust, especially if a vessel with quicklime or some hygroscopic material be put in the case.
Cases have considerable effect on the air, which moves with a pendulum and is flung off from it at each vibration; the going rate of a chronometer can be altered by removing the case. It is therefore desirable that cases enclosing pendulums should be roomy. Many people prefer to omit the air-tight case, and to keep a record of barometric, thermometric and hygrometric changes, applying corrections based on these to the times shown by the clock.
It was formerly usual to suspend pendulums by means of a single spring about ½ in. wide riveted with chops of metal. The upper chop had a pin driven through it, which rested in grooves so as to allow the pendulum to hang vertically. The Suspension of pendulums. best modern pendulums are now made with two parallel springs put a little less than an inch apart. The edges of the chops where the springs enter are slightly rounded so as to avoid too sharp bending of the springs. Suspension of pendulums on knife edges was tried by B. L. Vulliamy and others, but did not prove a success.
It was once thought that lenticular pendulum bobs resisted the air less than those of other shapes, but it was forgotten that their large surface offered more “skin friction.” They are now no longer used, nor are spheres on account of difficulty of construction. A cylinder is the best form of bob; it is sometimes rounded at the top and bottom.
Escapements.—The term escapement is applied to any arrangement by which, as the wheels rotate, periodic impulses are given to the pendulum, while at the same time the motion of the wheels is arrested until the vibration of the pendulum has been completed. It thus serves as a mechanism for both counting and impelling. Since the vibrations of a pendulum through small arcs are performed in times independent of the length of the arc, it follows that if a pendulum hanging at rest receive an impulse it will swing out and in again, and the time of its excursion outwards and of its return will remain the same whatever (within limits) be the arc of the swing, and whatever be the impulse given to it. If the impulse is big, it starts with a high velocity, but makes a larger excursion outwards, and the distance it has to travel counteracts its increase of speed, so that its time remains the same. Hence a pendulum, if free to swing outwards and in again, without impediment, will adapt the length of its swing to the impulse it has received, and any interference with it, as by the locking or unlocking of the escapement, will be far less deleterious to its isochronism when such interference occurs at the middle of its path rather than at the ends. It follows that the best escapement will be one which gives an impulse to the pendulum for a short period at the lowest point of its path, and then leaves it quite free to move as it chooses until the time comes for the next impulse.
But a pendulum is not quite truly isochronous, and has its time slightly affected by an increase of its arc; it is therefore desirable that the impulses given to it shall always be equal. If the escapement forms the termination of a clock-train impelled by a weight, the driving force of the escapement is apt to vary according to the friction of the wheels, while every change in temperature causes a difference in the thickness of the oil. It is therefore desirable, if possible, to secure uniformity of impulse—say, by causing the train of wheels to lift up a certain specified weight, and let it drop on the pendulum at regular intervals, or by some equivalent method.
The two requirements above stated have given rise respectively to what are known as detached escapements, and remontoires, which will be described presently. In the first place, however, it is desirable to describe the principal forms of escapement in ordinary use.
The balance escapement, which has been already mentioned, was in use before the days of pendulums. It was to a Balance escapement. balance escapement that Huygens applied the pendulum, by removing the weight from one arm and increasing the length of the other arm.
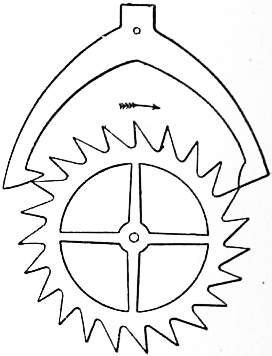 |
| Fig. 8.—Anchor or Recoil Escapement. |
 |
| Fig. 9.—Dead Escapement. |
Very shortly afterwards R. Hooke invented the anchor or recoil escapement. This is represented in fig. 8, where a tooth of the escape-wheel is just escaping from the right pallet, and another tooth at the same time falls upon the left-hand pallet at Anchor escapement. some distance from its point. As the pendulum moves on in the same direction, the tooth slides farther up the pallet, thus producing a recoil, as in the crown-wheel escapement. The acting faces of the pallets should be convex. For when they are flat, and of course still more when they are concave, the points of the teeth always wear a hole in the pallets at the extremity of their usual swing, and the motion is obviously easier and therefore better when the pallets are made convex; in fact, they then approach more nearly to the “dead” escapement, which will be described presently. The effect of some escapements is not only to counteract the circular error, or the natural increase of the time of a pendulum as the arc increases, but to over-balance it by an error of the contrary kind. The recoil escapement does so; for it is almost invariably found that whatever may be the shape of these pallets, the clock loses as the arc of the pendulum falls off, and vice versa. It is unfortunately impossible so to arrange the pallets that the circular error may be thus exactly neutralized, because the escapement error depends, in a manner reducible to no law, upon variations in friction of the pallets themselves and of the clock train, which produce different effects; and the result is that it is impossible to obtain very accurate time-keeping from any clock of this construction. The point in which the anchor escapement was superior to all that had gone before, was that it would work well with a small arc of swing of the pendulum. The balance escapement, even when adapted to a pendulum, necessitated a swing of some 20°, and hence the circular error, that is to say, the deviation of the path from a true cycloid, was considerable. But with an anchor escapement the pendulum swing need be only 3° or 4°. On the other hand, it violates the conditions above laid down for a perfect escapement, inasmuch as the pendulum is never free, but at the end of its swing is still operated on by the escapement, which it causes to recoil.
To get rid of this defect the dead escapement, or, as the French call it, l’échappement à repos, was invented by G. Graham. It is represented in fig. 9. It will be observed that the teeth of the scape-wheel have their points set the opposite way Dead escapements. to those of the recoil escapement. The tooth B is here represented in the act of dropping on to the right-hand pallet as the tooth A escapes from the left pallet. But instead of the pallet having a continuous face as in the recoil escapement, it is divided into two, of which BE on the right pallet, and FA on the left, are called the impulse faces, and BD, FG, the dead faces. The dead faces are portions of circles (not necessarily of the same circle), having the axis of the pallets C for their centre; and the consequence evidently is, that as the pendulum goes on, carrying the pallet still nearer to the wheel than the position in which a tooth falls on to the corner A or B of the impulse and the dead faces, the tooth still rests on the dead faces without any recoil, until the pendulum returns and lets the tooth slide down the impulse face, giving the impulse to the pendulum as it goes. In order to diminish the friction and the necessity for using oil as far as possible, the best clocks are made with jewels (sapphires are the best for the purpose) let into the pallets.
The pallets are generally made to embrace about one-third of the circumference of the wheel, and it is not at all desirable that they should embrace more; for the longer they are, the longer is the run of the teeth upon them, and the greater the friction. In some clocks the seconds hand moves very slowly and rests a very short time; this shows that the impulse is long in proportion to the arc of swing. In others the contrary is the case. A not uncommon proportion is that out of a total arc of swing of 3°, 2°, or about one degree on each side of the vertical, are occupied in receiving the impulse. In other words, the points F and A should subtend an angle of 2° at the centre C. It is not to be forgotten that the scape-wheel tooth does not overtake the face of the pallet immediately, on account of the moment of inertia of the wheel. The wheels of astronomical clocks, and indeed of all English house clocks, are generally made too heavy, especially the scape-wheel, which, by increasing the moment of inertia, causes a part of the work to be lost in giving blows, instead of being all used up in gentle pushes.
 |
| Fig. 10.—Pin-Wheel Escapement. |
A very useful form of the dead escapement, which is adopted in many of the best turret clocks, is called the “pin-wheel escapement.” Fig. 10 will sufficiently explain its action and construction. Its advantages are—that it does not require so much accuracy as the other; if a pin gets broken it is easily replaced, whereas in the other the wheel is ruined if the point of a tooth is injured; a wheel of given size will work with more pins than teeth, and therefore a train of less velocity will do, and that sometimes amounts to a saving of one wheel in the train, and a good deal of friction; and the blow on both pallets being downwards, instead of one up and the other down, the action is more steady; all which things are of more consequence in the heavy and rough work of a turret clock than in an astronomical one. It has been found expedient to make the dead faces not quite dead, but with a very slight recoil, which rather tends to check the variations of arc, and also the general disposition to lose time if the arc is increased; when so made the escapement is generally called “half-dead.”
In the dead escapement, during each excursion of the pendulum the repose surface of the pallets rubs against the points of the teeth of the scape-wheel. Thus the pendulum is subject to a constant retardation by friction. Curiously enough, this friction, which at first sight might appear a defect, is an advantage, and to a large extent accounts for the excellence of the escapement. For if the driving force of the clock is increased so that the impulse on the pallets is greater, the velocity of the pendulum is increased. But this very increase of the driving force causes a greater pressure of the teeth of the scape-wheel on the rest-faces of the pallets, and hence counteracts the increased drive of the pendulum by an increased frictional retardation. If the clock weight be enormously increased, the frictional retardation becomes increased relatively in a greater proportion than the drive, so that as the weight of the clock is increased the pendulum’s time of vibration is first diminished, until at last a neutral point is reached and finally the increased loading of the clock weight begins to make the time of vibration increase again. It is the neutral point which it is desirable to arrange for, and only trial and experience can so fit the shape and size of the pallets, scape-wheel and clock weight to one another, as to secure that a moderate variation of the driving power neither accelerates nor retards the motion of the pendulum, while at the same time such an arc of vibration is secured as shall be least subject to barometric error, and not have too great a circular error. The celebrated clockmaker B. L. Vulliamy (1780-1854) greatly improved Graham’s escapement by careful experiment, and other makers introduced further improvements into the shape of the scape-wheel and pallets, so that the best form of the deadbeat escapement is now fairly well determined and is given in books upon horology. For small clocks a little slope is given to the rest-faces so as to diminish the friction retardation. This is known as the half-dead escapement. The pin-wheel escapement, if properly constructed, is also “dead,” that is to say, the outward swing of the pendulum is unfettered except by the slight friction of the teeth against the dead faces of the pallets.
 |
| Fig. 11.—Riefler’s Escapement. |
In order to diminish the effect of the impact of the scape-wheel on the pallets, and of the crutch on the pendulum rod, the plan has been tried of making the crutch into an elastic spring. In theory this of course would not destroy the isochronism of the pendulum, for it would only be to apply upon the pendulum a force at right angles to the rod, and varying as the displacement. Hence any acceleration given by such a spring would, like the action of gravity, be harmonic, and it is an analytical principle that harmonic motions superposed on one another still remain harmonic. Hence, then, the action of a spring superadded upon the action of gravity on a pendulum still leaves the motion harmonic. But changes of temperature would affect the spring considerably. In the case of such a spring the repose faces of Graham’s escapement might be minimized and the escapement checked each side by a stop, so as to prevent the pallets from rubbing on the points of the scape-wheel. Graham’s escapement can, if well made, be arranged so as not to vary more than an average of 1⁄30 of a second from its mean daily rate, and this is so good a result that many people doubt whether further effort in the direction of inventing new escapements will result in any better form. Two adaptations of Graham’s escapement have been made, one by Clemens Riefler of Nesselwang, and the other by L. Strasser of Glashütte, Saxony, which give good results in practice. Riefler’s scheme is to mount the upper block, into which the suspension spring is fastened, upon knife edges, and rock it to and fro by the action of a modified Graham’s escapement, thus giving impulses to the pendulum. Fig. 11 shows the arrangement. PP are the agates upon which the knife edges CC rest. A is the anchor, RH the scape-wheels, and S the pallets.
Strasser’s clock is arranged on the same idea as that of Riefler, only that the rocking motion is given, not to the springs that carry the pendulum, but to a second pair of springs placed outside of them and parallel to them. The weight of the pendulum is therefore carried by an upper stationary block, but above that a second block is subjected to the rocking motion of the anchor. The general design is shown in fig. 12. The pallets are each formed of two stones, so contrived as to minimize the banging of the teeth of the scape-wheel. Both Riefler’s and Strasser’s clocks aim at haying a virtually free pendulum; in fact, they are in reality adaptations of the principle of the spring-clutch to Graham’s escapement. The weak point in both is the tampering with the suspension.
 |
| Fig. 12.—Strasser’s Escapement (Strasser & Rohde). |
The dead escapement is not, however, truly free. In order to make a free escapement it would be necessary to provide that as soon as the pendulum approached its centre position, some pin or projecting point upon it should free the Detached escapement. escapement wheel, a tooth of which should thus be enabled to leap upon the back of the pendulum, give it a short push, and then be locked until the pendulum had returned and again swung forward. An arrangement of this kind is shown in fig. 13. Let A be a block of metal fixed on the lower end of a pendulum rod. On the block let a small pall B be fastened, free to move round a centre C and resting against a stop D. Let E be a 4-leaved scape-wheel, the teeth of which as they come round rest against the bent pall GFL at G. The pall is prevented from flying too far back by a pin H, and kept up to position by a very delicate spring K. As soon as the pendulum rod, moving from left to right, has arrived at the position shown in the figure, the pall B will engage the arm FL, force it forwards, and by raising G will liberate the scape-wheel, a tooth of which, M, will thus close upon the heel N of the block A, and urge it forward. As soon, however, as N has arrived at G the tooth M will slip off the block A and rest on the pall G, and the impulse will cease. The pendulum is now perfectly free or “detached,” and can swing on unimpeded as far as it chooses. On its return from right to left, the pall B slips over the pall L without disturbing it, and the pendulum is still free to make an excursion towards the left. On its return journey from left to right the process is again repeated. Such an escapement operates once every 2 seconds. One made on a somewhat similar plan was applied to a clock by Robert-Houdin, about 1830, and afterwards by Mr Haswell, and another by Sir George Airy. But the principle was already an old one, as may be seen from fig. 14, which was the work of an anonymous maker in the 18th century. A consideration of this escapement will show that it is only the application of the detached chronometer escapement to a clock.

| Fig. 13.—Free Escapement. | Fig. 14.—Free Escapement (old form). |
Even detached escapements, however, are not perfect. In order that an escapement should be perfect, the impulse given to the pendulum should be always exactly the same. It may be asked why, if the time of oscillation of the pendulum be independent of the amplitude of the arc of vibration, and hence of the impulse, it is necessary that the impulse should be uniform. The answer is that the arc of vibration not being a true cycloid, as it should be if true isochronism is to be secured, but being the arc of a circle, any change of amplitude of vibration produces a change of time in the swing given by the formula 3⁄2(a² - b²) = loss in seconds per day, where a and b are the semi-arcs of vibration estimated in degrees. Thus 10’ increase of arc in a swing of 4°, that is to say, .1 in. increase of arc in a total arc of 2½ in., produces an error of about a second a day. Now cold weather, by making the oil thick and thus clogging the wheels, will easily produce such a change of arc; dust will also make a change even though the clock weight, acted on by gravity, still exerts a uniform pull. Besides, if the clock has work to do of a varying amount—as when the hands of a turret clock are acted on by a heavy wind pressure tending sometimes to retard them, sometimes to drive them on—then it is clear that the impulses given by the scape-wheel to the pendulum may be very unequal, and that the arc of vibration of the pendulum may thus be seriously affected and its isochronism disturbed.
To abolish errors arising from the changes in the force driving the escapement, what is known as the “remontoire” system was adopted. It first came into use for watches, which was perhaps natural, seeing that the driving force of a watch Remontoire. is not a uniform weight like that of a clock, but depends on springs, which are far less trustworthy. The idea of a remontoire is to disconnect the escapement from the clock train, and to give the escapement a driving power of its own, acting as directly as possible on the pallets without the intervention of a clock-train containing many wheels. The escapement is thus as it were made into a separate clock, which of course needs repeated winding, and this winding is effected by the clock-train. From this it results that variations in the force transmitted by the clock-train merely affect the speed at which the “rewinding” of the escapement is effected, but do not affect the force exerted by the driving power of the escapement.
There are several modes of carrying out this plan. The first of them is simply to provide the scape-wheel with a weight or spring of its own, which spring is wound up by the clock-train as often as it runs down. Contrivances of this kind are Train remontoires. called train remontoires. In arranging such a remontoire it is obvious that the clock-train must be provided with a stop to prevent it from overwinding the scape-wheel weight or spring, and further, that there must be on the scape-wheel some sort of stud or other contrivance to release the clock-train as soon as the scape-wheel weight or spring has run down and needs rewinding. We believe the first maker of a large clock with a train remontoire was Thomas Reid of Edinburgh, who described his apparatus in his book on Horology (1819). The scape-wheel was driven by a small weight hung by a Huygens’s endless chain, of which one of the pulleys was fixed to the arbor, and the other rode upon the arbor, with the pinion attached to it, and the pinion was driven and the weight wound up by the wheel below (which we will call the third wheel), as follows. Assuming the scape-wheel to turn in a minute, its arbor has a notch cut half through it on opposite sides in two places near to each other; on the arbor of the wheel, which turns in ten minutes, suppose, there is another wheel with 20 spikes sticking out of its rim, but alternately in two different planes, so that one set of spikes can only pass through one of the notches in the scape-wheel arbor, and the other set only through the other. Whenever, then, the scape-wheel completes a half-turn, one spike is let go, and the third wheel is able to move, and with it the whole clock-train and the hands, until the next spike of the other set is stopped by the scape-wheel arbor; at the same time the pinion on that arbor is turned half round, winding up the remontoire weight, but without taking its pressure off the scape-wheel. Reid says that, so long as this apparatus was kept in good order, the clock went better than it did after it was removed in consequence of its getting out of order from the constant banging of the spikes against the arbor.
 |
| Fig. 15.—Gravity Train Remontoire. |
A clock at the Royal Exchange, London, was made in 1844 on the same principle, except that, instead of the endless chain, an internal wheel was used, with the spikes set on it externally, which is one of the modes by which an occasional secondary motion may be given to a wheel without disturbing its primary and regular motion. The following is a more simple arrangement of a gravity train remontoire, much more frequently used in principle. Let E in fig. 15 be the scape-wheel turning in a minute, and e its pinion, which is driven by the wheel D having a pinion d driven by the wheel C, which we may suppose to turn in an hour. The arbors of the scape-wheel and hour-wheel are distinct, their pivots meeting in a bush fixed somewhere between the wheels. The pivots of the wheel D are set in the frame AP, which rides on the arbors of the hour-wheel and scape-wheel, or on another short arbor between them. The hour-wheel also drives another wheel G, which again drives the pinion f on the arbor which carries the two arms fA, fB; and on the same arbor is set a fly with a ratchet, like a common striking fly, and the numbers of the teeth are so arranged that the fly will turn once for each turn of the scape-wheel. The ends of the remontoire arms fA, fB are capable of alternately passing the notches cut half through the arbor of the scape-wheel, as those notches successively come into the proper position at the end of every half-minute; as soon as that happens the hour-wheel raises the movable wheel D and its frame through a small angle; but, nevertheless, that wheel keeps pressing on the scape-wheel as if it were not moving, the point of contact of the wheel C and the pinion d being the fulcrum or centre of motion of the lever AdP. It will be observed that the remontoire arms fA, fB have springs set on them to diminish the blow on the scape-wheel arbor, as it is desirable not to have the fly so large as to make the motion of the train, and consequently of the hands, too slow, to be distinct.
Another kind of remontoire is on the principle of one bevelled wheel lying between two others at right angles to it. The first of the bevelled wheels is driven by the train, and the third is fixed to the arbor of the scape-wheel; and the intermediate bevelled wheel, of any size, rides on its arbor at right angles to the other two arbors which are in the same line. The scape-wheel will evidently turn with the same average velocity as the first bevelled wheel, though the intermediate one may move up and down at intervals. The transverse arbor which carries it is let off and lifted a little at half-minute intervals, as in the remontoire just now described; and it gradually works down as the scape-wheel turns under its pressure, until it is freed again and lifted by the clock-train.
 |
| Fig. 16.—Spring Remontoire. |
In all these gravity remontoires, however, only the friction of the heavy parts of the train and the dial-work is got rid of, and the scape-wheel is still subject to the friction of the remontoire wheels, which, though much less than the other, is still something considerable. Accordingly, attempts have frequently been made to drive the scape-wheel by a spiral spring, like the mainspring of a watch. One of these was described in the 7th edition of this encyclopaedia; and Sir G. Airy invented another on the same principle, of which one specimen is still going well. One of the best forms of such a remontoire is shown in fig. 16, in which A, B, D, E, e, f are the same things as in fig. 15. But e, the scape-wheel pinion, is no longer fixed to the arbor, nor does it ride on the arbor, as had been the case in all the previous spring remontoires, thereby producing probably more friction than was saved in other respects; but it rides on a stud k, which is set in the clock frame. On the face of the pinion is a plate, of which the only use is to carry a pin h (and consequently its shape is immaterial), and in front of the plate is set a bush b, with a hole through it, of which half is occupied by the end of the stud k, to which the bush is fixed by a small pin, and the other half is the pivot-hole for the scape-wheel arbor. On the arbor is set the remontoire spring s (a moderate-sized musical-box spring is generally used), of which the outer end is bent into a loop to take hold of the pin h. In fact, there are two pins at h, one a little behind the other, to keep the coils of the spring from touching each other. Now, it is evident that the spring may be wound up half or a quarter of a turn at the proper intervals without taking the force off the scape-wheel, and also without affecting it by any friction whatever. When the scape-wheel turns in a minute, the letting-off would be done as before described, by a couple of notches in the scape-wheel arbor, through which the spikes A, B, as in fig. 15, would pass alternately. During the half-minute that the spring is running down the impulse on the pendulum constantly diminishes; but this error is small if the spring be properly shaped, and besides, being periodic, does not affect the average time-keeping of the clock. It would be inadmissible in astronomical clocks where each particular second has always to be true. In clocks with only three wheels in the train it is best to make the scape-wheel turn in two minutes. In that case four notches and four remontoire arms are required, and the fly makes only a quarter of a turn. Lord Grimthorpe made the following provision for diminishing the friction of the letting-off work. The fly pinion f has only half the number of teeth of the scape-wheel pinion, being a lantern pinion of 7 or 8, while the other is a leaved pinion of 14 or 16, and therefore the same wheel D will properly drive both, as will be seen hereafter. The scape-wheel arbor ends in a cylinder about 5⁄8 in. in diameter, with two notches at right angles cut in its face, one of them narrow and deep, and the other broad and shallow, so that a long and thin pin B can pass only through one, and a broad and short pin A through the other. Consequently, at each quarter of a turn of the scape-wheel, the remontoire fly, on which the pins A, B are set on springs, as in fig. 15, can turn half round. It is set on its arbor f by a square ratchet and click, which enables the spring to be adjusted to the requisite tension to obtain the proper vibration of the pendulum. A better construction, afterwards introduced, is to make the fly separate from the letting-off arms, whereby the blow on the cylinder is diminished, the fly being allowed to go on as in the gravity escapement. It should be observed, however, that even a spring remontoire requires a larger weight than the same clock without one; but as none of that additional force reaches the pendulum, that is of no consequence. The variation of force of the remontoire spring from temperature, as it only affects the pendulum through the medium of the dead escapement, is far too small to produce any appreciable effect; and it is found that clocks of this kind, with a compensated pendulum 8 ft. long, and weighing about 2 cwt., will not vary above a second a month, if the pallets are kept clean and well oiled. No turret clock without either a train remontoire or a gravity escapement will approach that degree of accuracy.
The introduction of this remontoire led to another very important alteration in the construction of large clocks. Hitherto it had always been considered necessary, with a view to diminish the friction as far as possible, to make the wheels of brass or gun-metal, with the teeth cut in an engine. The French clockmakers had begun to use cast iron striking parts, and cast iron wheels had been occasionally used in the going part of inferior clocks for the sake of cheapness; but they had never been used in any clock making pretensions to accuracy. But in consequence of the success of a clock shown in the 1851 Exhibition, it was determined by Sir G. Airy and Lord Grimthorpe (then E. Denison), who were jointly consulted by the Board of Works about the great Westminster clock in 1852, to alter the original requisition for gun-metal wheels there to cast iron. But cast iron wheels must drive cast iron pinions, for they will wear out steel.

| Fig. 17.—Mudge’s Gravity Escapement. | Fig. 18.—Bloxam’s Gravity Escapement. |
The next kind of remontoire still leaves the scape-wheel linked up with the clock-train, but makes it wind up the pallets which are held raised up till their action is wanted, when they are allowed to drop gently on the crutch or the pendulum rod. In this case the Gravity escapements. two arms of the anchor are usually divided and mounted on separate shafts so as to act independently. This idea was first started by Thomas Mudge (1717-1794) and Alexander Cumming (1733-1814). Mudge’s escapement is shown in fig. 17. The tooth A of the scape-wheel is resting against the stop or detent a at the end of the pallet CA, from the axis or arbor of which descends the half-fork CP to touch the pendulum. From the other pallet CB descends the other half-fork CO. The two arbors are set as near the point of suspension, or top of the pendulum spring, as possible. The pendulum, as here represented, must be moving to the right, and just leaving contact with the left pallet and going to take up the right one; as soon as it has raised that pallet a little it will evidently unlock the wheel and let it turn, and then the tooth B will raise the left pallet until it is caught by the stop b on that pallet, and then it will stay until the pendulum returns and releases it by raising that pallet still higher. Each pallet therefore descends with the pendulum to a lower point than that where it is taken up, and the difference between them is supplied by the lifting of each pallet by the clock, which does not act on the pendulum at all; so that the pendulum is independent of all variations of force and friction in the train. This escapement is said by Lord Grimthorpe, in his Rudimentary Treatise on Clocks, first published in 1850, to be liable to trip, the pallets being apt to be jerked by the pendulum, so that the teeth slip past the hook, and the wheel flies round. This, however, appears entirely a matter of construction. The really weak point is that while the impulses on the pendulum due to the gravitational fall of the arms are uniform, the force which has to be exercised by the pendulum in unlocking them from the scape-wheel varies with the pressure of the clock-train. Hence we miss the compensation which is so beautiful a result of Graham’s escapement. To avoid this, J. M. Bloxam, a barrister, proposed about the middle of the 19th century his legged gravity escapement (fig. 18). By this arrangement the parts of the scape-wheel which lifted the gravity arms were brought as near to the axis of the scape-wheel as possible, while the locking arms were brought as far from the axis as possible so that the pressure should be light. The pallet arbors were cranked, to embrace the pendulum-spring, so that their centres of motion might coincide with that of the pendulum as nearly as possible—perhaps an unnecessary refinement; at least the three-legged and four-legged gravity escapements answer very well with the pallet arbors set on each side of the top of the spring. The size of the wheel determines the length of the pallets, as they must be at such an angle to each other that the radii of the wheel when in contact with each stop may be at right angles to the pallet arm; and therefore, for a wheel of this size, the depth of locking can only be very small. The pinion in Bloxam’s clock only raises the pallet through 40′ at each beat; i.e. the angle which we call γ, viz. the amplitude of the pendulum when it begins to lift the pallet, is only 20′; and probably, if it were increased to anything like a/√2, where a is the semiarc of swing, the escapement would trip immediately. The two broad pins marked E, F, are the fork-pins, and A and B are the stops. The clock which Bloxam had went very well; but it had an extremely fine train, with pinions of 18; and nobody else appears to have been able to make one to answer.
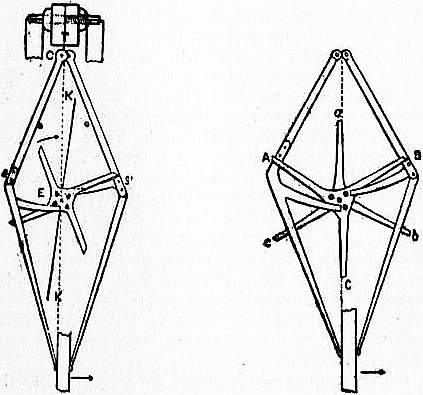
| Fig. 19.—Four-legged Gravity Escapement. | Fig. 20.—Double Three-legged Escapement. |
Bloxam’s escapement was modified in form by Lord Grimthorpe, his chief improvement being the addition of a fly vane, which, however, had previously been used for remontoires to steady the motion. He tried various modifications of construction, but finally adopted the “four-legged” and “double-three-legged” forms as being the most satisfactory, the former for regulators and the latter for large clocks. Fig. 19 is a back view of the escapement part of an astronomical clock with the four-legged wheel; seen from the front the wheel would turn the other way. The long locking teeth are made about 2 in. long from the centre, and the lifting pins, of which four point forwards while four other intermediate ones point backwards, are at not more than 1⁄30 of the distance between the centres EC, of the scape-wheel and pallets; or rather C is the top of the pendulum spring to which the pallets Cs, Cs′ converge, though the resultant of their action is a little below C. It is not worth while to crank them as Bloxam did, in order to make them coincide exactly with the top of the pendulum, as the friction of the beat pins on the pendulum is insignificant, and even then would not be quite destroyed. The pallets are not in the same plane, but one is behind and the other in front of the wheel, with one stop pointing backwards and the other forwards to receive the teeth alternately—it does not matter which; in this figure the stop s is behind and the stop s’ forward. The pendulum is now going to the right, and just beginning to lift the right pallet and free the stop s′; then the wheel will begin to turn and lift the other pallet by one of the pins which is now lowest, and which moves through 45° across the line of centres, and therefore lifts with very little friction. It goes on till the tooth now below s reaches s and is stopped there. Meanwhile the pallet Cs’ goes on with the pendulum as far as it may go, to the end of the arc which we have called α, starting from γ; but it falls with the pendulum again, not only to γ but to -γ on the other side of 0, so that the impulse is due to the weight of each pallet alternately falling through 2γ; and the magnitude of the impulse also depends on the obliqueness of the pallet on the whole, i.e. on the distance of its centre of gravity from the vertical through C. The fly KK′ is set on with a friction spring like the common striking-part fly, and should be as long as there is room for, length being much more effective than width.
The double three-legged gravity escapement, which was first used in the Westminster clock, is shown in fig. 20. The principle of it is the same as of the four-legs; but instead of the pallets being one behind and the other in front of the wheel, with two sets of lifting pins, there are two wheels ABC, abc, with the three lifting pins and the two pallets between them like a lantern pinion. One stop B points forward and the other A backward. The two wheels have their teeth set intermediately or 60° apart, though that is not essential, and the angle of 120° may be divided between them in any other proportions, as 70° and 50°, and in that way the pallets may be still more oblique than 30° from the vertical, which, however, is found enough to prevent tripping even if the fly gets loose, which is more likely to happen from carelessness in large clocks than in astronomical ones.
Of course the fly for those escapements in large clocks, with weights heavy enough to drive the hands in all weather, must be much larger than in small ones. For average church clocks with 1¼ sec. pendulum the legs of the scape-wheels are generally made 4 in. long and the fly from 6 to 7 in. long in each vane by 1¼ or 1½ wide. For 1½ sec. pendulums the scape-wheels are generally made 4½ radius. At Westminster they are 6 in.
Lord Grimthorpe considered that these escapements act better, especially in regulators, if the pallets do not fall quite on the lifting pins, but on a banking, or stop at any convenient place, so as to leave the wheel free at the moment of starting; just as the striking of a common house clock will sometimes fail to start unless the wheel with the pins has a little run before a pin begins to lift the hammer. The best way to manage the banking is to make the beat-pins long enough to reach a little way behind the pendulum, and let the banking be a thin plate of any metal screwed adjustably to the back of the case. This plate cannot well be shown in the drawings together with the pendulum, which, it may be added, should take up one pallet just when it leaves the other.
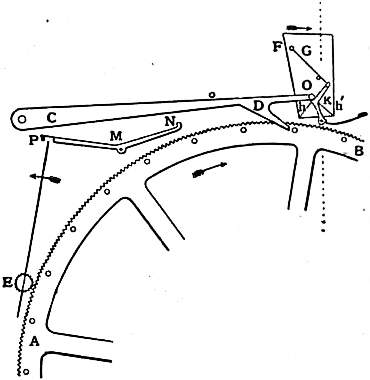 |
| Fig. 21.—Chronometer Spring Remontoire. |
In chronometer spring remontoires the pendulum, as it goes by, flips a delicate spring and releases a small weight or spring which has been wound up in readiness by the action of the scape-wheel and which by leaping on to the pendulum gives it Chronometer spring remontoire. a push. One on this principle made about the middle of the 19th century by Robert Houdin is to be seen at the Conservatoire des Arts et Métiers. It is very complicated. The following is more simple. In fig. 21 a scape-wheel AB has 30 pins and 360 teeth. It is engaged with a fly vane EP mounted on a pinion of 12 teeth. Each pin as it passes raises an impulse arm CD which is hooked upon a detent K. A pall NM then engages the fly vane and prevents the scape-wheel from moving farther. The impulse arm being now set, as the plate F attached to the lower end of the pendulum flies past from left to right a pall G knocks aside the detent K, and allows a pin O projecting from the end of the impulse arm to fall upon an inclined pallet h, which is thus urged forward. As soon as the pallet has left the pin, the impulse arm in its further fall strikes N, which disengages the pall at P and allows the scape-wheel to move on and again wind up the impulse arm CD, which is then again locked by the detent K. On the return journey of the pendulum the light pall G, which acts the part of a chronometer spring, flips over the detent. The pallet is double sided, h and h′, so that if by chance the clock runs down while the pendulum swings from left to right the impulse arm will be simply raised and not smashed. It has a flat apex, on which the pin falls before descending. The impulse given depends on the weight of the impulse arm and may be varied at pleasure. The work done in unlocking the detent is invariable, as it depends on the pressure of the fly vane at P and is independent of the clock-train. The duration of the impulse is very short—only about 1⁄10 of the arc of swing. It is given exactly at the centre of the swing, and when not under impulse the pendulum is detached.
Clock Wheels.—Since, as we have seen, any increase in the arc of a pendulum is accompanied by a change in its going rate, it is very desirable to keep the force which acts on the pendulum uniform. This in fact is the great object of the best escapements. Inasmuch as the impulse on the pendulum, derived from the work done by a falling weight or an unwinding spring, is transmitted through a train of wheels, it is desirable that that transmission should be as free from friction and as regular as possible. This involves care in the shaping of the teeth. The object to be aimed at is that as the wheel turns round the ratio of the power of the driver to that of the driven wheel (“runner” or “follower”) should never vary. That is to say, whether the back part of the tooth of the driver is acting on the tip of the tooth of the follower, or the tip of the driver is acting on the back part of the tooth of the follower, the leverage ratio shall always be uniform. For simplicity of manufacture the pinion wheels are always constructed with radial leaves, so that the surface of each tooth is a plane passing through the axis of the wheel. The semicircular rounding of the end of the tooth is merely ornamental. The question therefore is, suppose that it is desired by means of a tooth on a wheel to push a plane round an axis, what is the shape that must be given to that tooth in order that the leverage ratio may remain unaltered?

| Fig. 22.—Cam and Plane. | Fig. 23. |
If a curved surface, known as a “cam,” press upon a plane one, both being hinged or centred upon pivots A and B respectively (fig. 22), then the line of action and reaction at D, the point where they touch, will be perpendicular to their Epicycloidal teeth. surfaces at the point of contact—that is perpendicular to BD, and the ratio of leverage will obviously be AE:BD, or AC:CB. Hence to cause the leverage ratio of the cam to the plane always to remain unaltered, the cam must be so shaped that in any position the ratio AC:CB will remain unchanged. In other words the shape of the cam must be such that, as it moves and pushes BD before it, the normal at the point of contact must always pass through the fixed point C.
 |
| Fig. 24. |
If a circle PMB roll upon another circle SPT (fig. 23) any point M on it will generate an epicycloid MN. The radius of curvature of the curve at M will always be MP, for the part at M is being produced by rotation round the point P. It follows that a line from B to M will always be tangential to the epicycloid. If the epicycloid be a cam moving as a centre round the centre R (not shown in the figure) of the circle SPT, the leverage it will exert upon a plane surface BM moving round a parallel axis at B, will always be as BP to PR, that is, a constant; whence MN is the proper shape of a tooth to act on a pinion with radial arms and centred at B. In designing a pair of wheels to transmit motion, which is to be multiplied say 6 times in the transmission (about the usual ratio for clock wheels), if we take two circles (called the “pitch circles”) touching one another with radii as 1:6, then the circumference of the smaller will roll 6 times round that of the larger. The smaller wheel will have a number of teeth, say 8 to 16, each of them being sectors of the circle (fig. 24). If there are 16 teeth, then on the surface of the driving wheel there will be 96 teeth. Each of these teeth will be shaped as the curve of an epicycloid formed by the rolling on the big circle of a circle whose diameter is the radius of the pitch circle of the pinion. Points of the teeth so formed are cut off, so as to allow of the pinion having a solid core to support it, and gaps are made into the pitch circle to admit the rounded ends of the leaves of the pinon wheel. Thus a cog-wheel is shaped out.
Clock wheels are made of hard hammered brass cut out by a wheel cutting machine. This machine consists of a vertical spindle on the top of which the wheel to be cut is fixed on a firmly resisting plate of metal of slightly smaller diameter, so as to allow the wheel to overlap. A cutter with the edges most delicately ground to the exact shape of the gap between two teeth is caused to rotate 3000 - 4000 times a minute, and brought down upon the edge of the wheel. The shavings that come off are like fine dust, but the cutter is pushed on so as to plunge right through the rim of the wheel in a direction parallel to the axis. In this way one gap is cut. The vertical spindle is now rotated one division, by means of a dividing plate, and another tooth is cut, and so the operation goes on round the wheel.
It is not desirable in clocks that the pinion wheels which are driven should have too few teeth, for this throws all the work on a pair of surfaces before the centres and is apt to produce a grinding motion. Theoretically the more leaves a pinion has the better. Pinions can be made with leaves of thin steel watch-spring. In this case quite small pinions can have 20 leaves or more. The teeth in the driving wheels then become mere notches for which great accuracy of shape is not necessary. Such wheels are easy to make and run well. Lantern pinions are also excellent and are much used in American clocks. They are easy to make in an ordinary lathe. The cog-wheels must, however, be specially shaped to fit them. They consist of a number of round pins arranged in a circle round the axis of the wheel and parallel to it. The ends are secured in flanges like the wires of a squirrel cage. The teeth of cog-wheels engage them and thus drive the wheel round. They were much used at one time but are now falling out of favour again.
It is possible to make toothed wheels that drive with perfect uniformity by using for the curve of the teeth involutes of circles. These involutes are traced out by a point on a string that is gradually unwound from a circle. They are Involute teeth. in fact epicycloids traced by a rolling circle of infinite radius, i.e. a straight line. Involute teeth have the advantage that they roll on one another instead of sliding. When badly made they put considerable strain on the axes or shafts that carry them. Hence they have not been regarded with great favour by clockmakers.
By the pitch of a wheel is meant the number of teeth to the inch of circumference or diameter of the wheel; the former is called the circumferential pitch, the latter the diametral pitch. Thus if we say that a wheel has Pitch. 40 diametral pitch we mean that it has 40 teeth to each inch of diameter. The circumferential pitch is of course got by dividing the diametral pitch by π. Wheel-cutters are made for all sizes of pitches. If it were needed to make a pair of wheels the ratio of whose motion was say 6:1 and we determined to use a diametral pitch of 30 to the inch, that is teeth about 1⁄10 in. wide at the base, and if the smaller circle were to have 20 teeth, we should need a blank of a diameter of 20⁄30 + 2⁄30 = 22⁄30 in. for the smaller wheel, and one of 120⁄30 + 2⁄30 = 122⁄30 in. for the larger wheel which would have 120 teeth to the inch and be 4.06 in diameter to the tips of the teeth. The smaller toothed wheel would be .73 of an inch in diameter over all. The pitch circles of the wheels would be 2⁄3 and 4 in. respectively. For fine wheel work, where the driver is always much larger than the driven wheel, the epicycloidal tooth appears preferable, as it is generally considered to put less side strain on the pinion wheel. But the relative merits of the two systems have never been properly tested for clock work.
Going Barrels.—A clock which is capable of going accurately must have some contrivance to keep it going while it is being wound up. In the old-fashioned house clocks, which were wound up by merely pulling one of the strings, and in which one such winding served for both the going and striking parts, this was done by what is called the endless chain of Huygens, which consists of a string or chain with the ends joined together, and passing over two pulleys on the arbors of the great wheels, with deep grooves and spikes in them, to prevent the chain from slipping. In one of the two loops or festoons which hang from the upper pulleys is a loose pulley without spikes, carrying the clock-weight, and in the other a small weight only heavy enough to keep the chain close to the upper pulleys. Now, suppose one of those pulleys to be on the arbor of the great wheel of the striking part, with a ratchet and click, and the other pulley fixed to the arbor of the great wheel of the going part; then (whenever the clock is not striking) the weight may be pulled up by pulling down that part of the string which hangs from the other side of the striking part; and yet the weight will be acting on the going part all the time. It would be just the same if the striking part and its pulley were wound up with a key, instead of the string being pulled, and also the same, if there were no striking part at all, but the second pulley were put on a blank arbor, except that in that case the weight would take twice as long to run down, supposing that the striking part generally requires the same weight × fall as the going part.
 |
| Fig. 25.—Harrison’s Going-Ratchet. |
This kind of going barrel, however, is evidently not suited to the delicacy of an astronomical clock; and Harrison’s going ratchet is now universally adopted in such clocks, and also in chronometers and watches for keeping the action of the train on the escapement during the winding. Fig. 25 (in which the same letters are used as in the corresponding parts of fig. 3) shows its construction. The click of the barrel-ratchet R is set upon another larger ratchet-wheel with its teeth pointing the opposite way, and its click rT is set in the clock frame. That ratchet is connected with the great wheel by a spring ss’ pressing against the two pins s in the ratchet and s’ in the wheel. When the weight is wound up (which is equivalent to taking it off), the click Tr prevents that ratchet from turning back or to the right; and as the spring ss’ is kept by the weight in a state of tension equivalent to the weight itself it will drive the wheel to the left for a short distance, when its end s is held fast, with the same force as if that end was pulled forward by the weight; and as the great wheel has to move very little during the short time the clock is winding, the spring will keep the clock going long enough.
In the commoner kind of turret clocks a more simple apparatus is used, which goes by the name of the bolt and shutter, because it consists of a weighted lever with a broad end, which shuts up the winding-hole. When it is lifted a spring-bolt attached to the lever, or its arbor, runs into the teeth of one of the wheels, and the weight of the lever keeps the train going until the bolt has run itself out of gear. Clocks are not always driven by weights. When accuracy is not necessary, but portability is desirable, springs are used. The old form of spring became weaker as it was unwound and necessitated the use of a device called a fusee or spiral drum. This apparatus will be found described in the article Watch.
Striking Mechanism.—There are two kinds of striking work used in clocks. The older of them, the locking-plate system, which is still used in most foreign clocks, and in turret clocks in England also, will not allow the striking of any hour to be either omitted or repeated, without making the next hour strike wrong; whereas in the rack system, which is used in all English house clocks, the number of blows to be struck depends merely on the position of a wheel attached to the going part, and therefore the striking of any hour may be omitted or repeated without deranging the following ones. We shall only describe the second of these, which is the more usual in modern timepieces.
Fig. 26 is a front view of a common English house clock with the face taken off, showing the repeating or rack striking movement. Here, as in fig. 3, M is the hour-wheel, on the pipe of which the minute-hand is set, N the reversed hour-wheel, and n its pinion, driving the 12-hour wheel H, on whose socket is fixed what is called the snail Y, which belongs to the striking work exclusively. The hammer is raised by the eight pins in the rim of the second wheel in the striking train, in the manner which is obvious.
 |
| Fig. 26.—Front view of common English House Clock. |
The hammer does not quite touch the bell, as it would jar in striking if it did, and prevent the full sound. The form of the hammer-shank at the arbor where the spring S acts upon it is such that the spring both drives the hammer against the bell when the tail T is raised, and also checks it just before it reaches the bell, the blow on the bell thus being given by the hammer having acquired momentum enough to go a little farther than its place of rest. Sometimes two springs are used, one for impelling the hammer, and the other for checking it. But nothing will check the chattering of a heavy hammer, except making it lean forward so as to act, partially at least, by its weight. The pinion of the striking-wheel generally has eight leaves, the same number as the pins; and as a clock strikes 78 blows in 12 hours, the great wheel will turn in that time if it has 78 teeth instead of 96, which the great wheel of the going part has for a centre pinion of eight. The striking-wheel drives the wheel above it once round for each blow, and that wheel drives a fourth (in which there is a single pin P), six, or any other integral number of turns, for one turn of its own, and that drives a fan-fly to moderate the velocity of the train by the resistance of the air, an expedient at least as old as De Vick’s clock in 1379.
The wheel N is so adjusted that, within a few minutes of the hour, the pin in it raises the lifting-piece LONF so far that that piece lifts the click C out of the teeth of the rack BKRV, which immediately falls back (helped by a spring near the bottom) as far as its tail V can go by reason of the snail Y, against which it falls; and it is so arranged that the number of teeth which pass the click is proportionate to the depth of the snail; and as there is one step in the snail for each hour, and it goes round with the hour-hand, the rack always drops just as many teeth as the number of the hour to be struck. This drop makes the noise of “giving warning.” But the clock is not yet ready to strike till the lifting piece has fallen again; for, as soon as the rack was let off, the tail of the gathering pallet G, on the prolonged arbor of the third wheel, was enabled to pass the pin K of the rack on which it was pressing before, and the striking train began to move; but before the fourth wheel had got half round, its pin P was caught by the end of the lifting-piece, which is bent back and goes through a hole in the plate, and when raised stands in the way of the pin P, so that the train cannot go on till the lifting-piece drops, which it does exactly at the hour, by the pin N then slipping past it. Then the train is free; the striking wheel begins to lift the hammer, and the gathering pallet gathers up the rack, a tooth for each blow, until it has returned to the place at which the pallet is stopped by the pin K coming under it. In this figure the lifting-piece is prolonged to F, where there is a string hung to it, as this is the proper place for such a string when it is wanted for the purpose of learning the hour in the dark, and not (as it is generally put) on the click C; for if it is put there and the string is held a little too long, the clock will strike too many; and if the string accidentally sticks in the case, it will go on striking till it is run down—neither of which things can happen when the string is put on the lifting-piece.
The snail is sometimes set on a separate stud with the apparatus called a star-wheel and jumper. On the left side of the frame we have placed a lever x, with the letters st below it, and si above. If it is pushed up to si, the other end will come against a pin in the rack, and prevent it from falling, and will thus make the clock silent; and this is much more simple than the old-fashioned “strike and silent” apparatus, which we shall therefore not describe, especially as it is seldom used now.
If the clock is required to strike quarters, a third “part” or train of wheels is added on the right hand of the going part; and its general construction is the same as the hour-striking part; only there are two more bells, and two hammers so placed that one is raised a little after the other. If there are more quarter-bells than two, the hammers are generally raised by a chime-barrel, which is merely a cylinder set on the arbor of the striking-wheel (in that case generally the third in the train), with short pins stuck into it in the proper places to raise the hammers in the order required for the tune of the chimes. The quarters are usually made to let off the hour, and this connexion may be made in two ways. If the chimes are different in tune for each quarter, and not merely the same tune repeated two, three and four times, the repetition movement must not be used for them, as it would throw the tunes into confusion, but the old locking-plate movement, as in turret clocks; and therefore, if we conceive the hour lifting-piece connected with the quarter locking-plate, as it is with the wheel N, in fig. 26, it is evident that the pin will discharge the hour striking part as the fourth quarter finishes.
But where the repetition movement is required for the quarters, the matter is not quite so simple. The principle of it may shortly be described thus. The quarters themselves have a rack and snail, &c., just like the hours, except that the snail is fixed on one of the hour-wheels M or N, instead of on the twelve-hour wheel, and has only four steps in it. Now suppose the quarter-rack to be so placed that when it falls for the fourth quarter (its greatest drop), it falls against the hour lifting-piece somewhere between O and N, so as to raise it and the click C. Then the pin Q will be caught by the click Qq, and so the lifting-piece will remain up until all the teeth of the quarter-rack are gathered up; and as that is done, it may be made to disengage the click Qq, and so complete the letting off the hour striking part. This click Qq has no existence except where there are quarters.
The method in which an alarum is struck may be understood by reference to either of the recoil escapements (figs. 1 and 7). If a short hammer instead of a long pendulum be attached to the axis of the pallets, and the wheel be driven with sufficient force, it will evidently swing the hammer rapidly backwards and forwards; and the position and length of the hammer-head may be so adjusted as to strike a bell inside, first on one side and then on the other. As to the mode of letting off the alarum at the time required: if it was always to be let off at the same time all that would be necessary would be to set a pin in the twelve-hour wheel at the proper place to raise the lifting-piece which lets off the alarum at that time. But as the time must be capable of alteration, this discharging pin must be set in another wheel (without teeth), which rides with a friction-spring on the socket of the twelve-hour wheel, with a small movable dial attached to it, having figures so arranged with reference to the pin that whatever figure is made to come to a small pointer set as a tail to the hour hand, the alarum shall be let off at that hour.
The watchman’s or tell-tale clock, used when it is desired to make sure of a watchman being on the spot and awake all the night, is a clock with a set of spikes, generally 48 or 96, sticking out all round the dial, and a handle somewhere in the case, by pulling which one of the spikes which is opposite to it, or to some lever connected with it is pressed in. This wheel of spikes is carried round with the hour-hand, which in these clocks is generally a twenty-four hour one. It is evident that every spike which is seen still sticking out in the morning indicates that at the particular time to which that spike belongs the watchman was not there to push it in—or at any rate, that he did not. At some other part of their circuit, the inner ends of the pins are carried over a roller or an inclined plane which pushes them out again ready for business the next night. The time at which workmen arrive at their work may be recorded by providing each of them with a numbered key with which he stamps his number on a moving tape, on which also the time is marked by a clock.
Church and Turret Clocks.—Seeing that a clock—at least the going part of it—is a machine in which the only work to be done is the overcoming of its own friction and the resistance of the air, it is evident that when the friction and resistance are much increased it may become necessary to resort to expedients for neutralizing their effects, which are not required in a smaller machine with less friction. In a turret clock the friction is enormously increased by the great weight of all the parts; and the resistance of the wind, and sometimes snow, to the motion of the hands, further aggravates the difficulty of maintaining a constant force on the pendulum; and besides that, there is the exposure of the clock to the dirt and dust which are always found in towers, and of the oil to a temperature which nearly or quite freezes it all through the usual cold of winter. This last circumstance alone will generally make the arc of the pendulum at least half a degree more in summer than in winter; and inasmuch as the time is materially affected by the force which arrives at the pendulum, as well as the friction on the pallets when it does arrive there, it is evidently impossible for any turret clock of the ordinary construction, especially with large dials, to keep any constant rate through the various changes of temperature, weather and dirt to which it is exposed. Hence special precautions, such as the use of remontoires and gravity escapements, have to be observed in the design of large clocks that have any pretensions to accuracy, in order to ensure that the arc of the pendulum is not affected by external circumstances, such as wind-pressure on the hands or dirt in the wheel-train. But such have been the improvements effected in electric clocks, that rather than go to the trouble and expense required by such precautions, it appears far preferable to keep an accurate time-piece in some sheltered position and use it with a source of electricity to drive the hands of the large dial.
Electrical Clocks.—One of the first attempts to apply electricity to clocks was made by Alexander Bain in 1840-1850. About the same time Sir C. Wheatstone, R. L. Jones, C. Shepherd, Paul Garnier and Louis Bréguet invented various forms of electrical time-keepers. It is not proposed here to go into the history of these abortive attempts. Those who desire to follow them may consult Bain, An Account of Some Applications of the Electric Fluid to the Useful Arts (1843) and Short History of Electric Clocks (1852); Sir Charles Wheatstone, Trade Circular of the British Telegraph Manufactory; C. Shepherd, On the Application of Electro-magnetism as a Motor for Clocks (1851), and a list of references in the Appendix to Tobler’s Die electrischen Uhren (Leipzig, 1883), and a list of books given by F. Hope Jones, Proc. Inst. Elec. Eng., 1900, vol. 29. The history of electrical clocks is a long and complicated matter, for there are some 600 or 700 patents for these clocks in Europe and America, some containing the germs of valuable ideas but most pure rubbish. All that can be done is to select one or two prominent types of each class and give a brief description of their general construction.
 |
| Fig. 27.—Turret Clock for Hidalgo, Mexico, driving four 8 ft. dials. |
 |
| Fig. 28. |
It is in the apparently simple matter of making and keeping the electrical contact that most of the systems of electrical time-keeping have failed, for want of attention to the essential conditions of the problem. In practice every metal is covered with a thin film of non-conducting oxide over which is another film of moisture, oil, dirt or air. Hence what is wanted is a good vigorous push of a blunted point or edge preferably obliquely upon a more or less yielding surface so as to get a rubbing action. Thus if the stiff spring a b (fig. 28) were stabbed down on the oblique surface C D a good contact would invariably result, provided that the metals employed were gold, platinum or some not easily oxidizable metal. Or again, if a mercury surface be simply touched with a pin, the slight sparking that is produced on making the current will soon form a little pile of dirty oxide at the point of entry, and the contact will frequently fail. If it be necessary to have a mercury contact, the pin must be well driven in below the surface of the mercury or else swept through it as an oar is swept through the water. Another form of electrical contact that acts well is a knife edge brought into contact with a series of fine elastic strips of metal laid parallel to one another like the fingers of a hand. The best metal for contacts, if they are to bear hard usage, is either silver or gold or a mixture of 40% iridium with 60% of platinum. A pressure of some 15 grammes, at least, is needful to secure a good contact.
As to the source of current for driving electrical clocks, if Leclanché cells be used they should preferably be kept in the open air under cover so as not to dry up. If direct electric current is available from electric light mains or the accumulators used for lighting a private house, so much the better. Of course the pressure of 50 or 100 volts used for lighting would be far too great for clock-driving, where only the pressure of a few volts is required. But it is easy by the insertion of suitable resistances, as for instance one or more incandescent lamps, to weaken down the pressure of the lighting system and make it available for electric clocks, bells or other similar purposes.
Electricity is applied to clocks in three main ways:—(1) in actuating timepieces which measure their own time and must therefore be provided with pendulums or balance wheels; (2) in reproducing on one or more dials the movements of the hands of a master clock, by the aid of electric impulses sent at regular intervals, say of a minute or a half-minute; and (3) in synchronizing ordinary clocks by occasional impulses sent from some accurate regulator at a distance.
Electrically driven timepieces may be divided under two heads:—(a) those in which the electric current drives either the pendulum or some lever which operates upon it, which lever or pendulum in turn drives the clock hands; and (b) those timepieces which are driven by a weight or spring which is periodically wound up by electricity—in fact electrical remontoires.
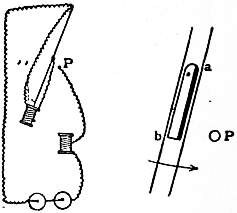 |
| Fig. 29.—Electrical Clock (faulty design). |
The simplest clock of the first character that could be imagined would be constructed by fastening an electromagnet with a soft iron core to the bottom of a pendulum, and causing it to be attracted as the pendulum swings by another electromagnet fixed vertically under it (fig. 29). As the pendulum approached the vertical and was say half an inch from its lowest point, the current would be switched on, and switched off as soon as the pendulum got to its lowest point. A very small attraction with this arrangement, probably about a grain weight, acting through the ½ in. would drive a heavy pendulum. A switch would have to be worked in connexion with the pendulum. A strip of ebonite with a small face of metal on the end of one side, such as a b (fig. 29) might be pivoted at one end on the pendulum with a weak spring to keep it where free along the rod. As the pendulum swung by this would be swept on its journey from left to right against a fixed pin P. This would complete the electric circuit down through the pendulum rod, round the coil on the bottom of the pendulum, through the switch into the pin P, thence through the fixed electromagnet, and so back to the battery. On the return journey no contact would be made because only the ebonite face of the switch would touch P. The pendulum would thus receive an impulse every other vibration. We have described this switch, not to advocate it, but to warn against its use. For the contact would be quite insufficient. In order that the switch might not unduly retard the pendulum it must be light, but this would make the pressure on P too light to be trustworthy. Moreover, the strength of the impulse would vary with the strength of the battery, and hence the arc would be repeatedly uneven.
 |
| Fig. 30.—Hipp Electrical Clock (Peyer, Favarger et Cie.). |
In contrast with this, let us consider a clock that is now giving excellent results at the Observatory of Neuchatel in Switzerland on Hipp’s system (La Pendule électrique de précision, Neuchatel, 1884 and 1891). The pendulum (fig. 30) consists of two rods of steel joined by four bridges, one just below the suspension spring, the next about 12 in. lower, the next about half way down, and the last supporting a glass vessel of mercury which forms the bob. On the third of them is placed an iron armature, which works between the poles of an electromagnet fixed to the case, and by which the pendulum is actuated. The circuit is closed and broken by a flipper, which is swayed to and fro by a block fixed to the pendulum at the second bridge. As long as the flipper is merely swayed, no contact takes place, but when the arc of vibration of the pendulum is diminished the flipper does not clear the block but is caught by a nick in it, and forced downwards. In this way the circuit is closed. Fig. 31 is a diagram of the apparatus. When the block g attached to the pendulum catches and presses down the flipper s, the lever l l is rocked over, so that a contact is made at k, and the current which enters the lever l through the knife edge m, runs through the second lever n n, down through the knife edge o, to the battery, and through the electromagnet b which causes the armature a to be attracted. As the block g goes on and releases s, the lever l again falls upon the rest p, the lever n follows it a part of the way till it is stopped by the contact q; this shortcircuits the electromagnet and prevents to a large extent the formation of an induced current. It is claimed that sparking is by this method almost entirely avoided. It is only when s is caught in the notch of the block g that s is pressed down, so that the electric attraction only takes place every few vibrations. This ingenious arrangement makes the working of the clock nearly independent of the strength of the battery, for if the battery is strong the impulses are fewer and the average arc remains the same. The clock is enclosed in an airtight glass case so as to avoid barometric error. It was tested in 1905 at the Neuchâtel observatory. In winter in a room of a mean temperature of 35° F. it was ¼ sec. too slow, in summer when the temperature was 70°, it was ½ sec. too fast. In the succeeding winter it became .53 sec. too slow again, thus gaining a little in summer and losing in winter. Its average variation from its daily rate was, however, only .033 sec.
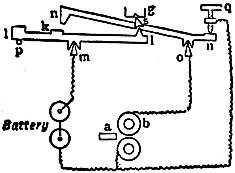 |
| Fig. 31.—Contact Arrangement of Hipp Clock. |
In another system originated by G. Froment, a small weight is raised by electricity and allowed to fall upon an arm sticking out at right angles to the pendulum in the plane of its motion, so as to urge it onwards. The weight is only allowed to rest on the arm during the downward swing of the pendulum. The method is not theoretically good, as the impulse is given at the end of the vibration of the pendulum instead of at its middle position.
In the clock invented by C. Féry (chef des travaux pratiques at the École de Physique et Chimie, Paris), an electric impulse is given at every vibration, not by a battery but by means of the uniform movement of an armature which is alternately pulled away from and pushed towards a permanent horseshoe magnet. Currents are thus induced in a bobbin of fine wire placed between the poles of the horseshoe magnet. The movements of the armature are produced by another horseshoe magnet actuated by the primary current from a battery which is turned on and off by the swinging of the pendulum. The energy of the induced current that drives the clock depends solely on the total movement of the armature, and is independent of whether that movement be executed slowly or rapidly, and therefore of the strength of the battery.
 |
| Fig. 32.—Hope Jones Electrical Remontoire. |
Electrical remontoires possess great advantages if they can be made to operate with certainty. For they can be made to wind up a scape-wheel just as is done in the case of the arrangement shown in fig. 16 so as to constitute a spring remontoire, or better still they can be made to raise a weight as in the case of the gravity train remontoire (fig. 15) but without the complications of wheel-work shown in that contrivance. Of this type one of the best known is that of H. Chesters Pond. A mainspring fixed on the arbor of the hour wheel is wound up every hour by means of another toothed wheel riding loose on the same arbor and driven by a small dynamo, to which the other end of the mainspring is attached. As soon as the hour wheel has made one revolution (driven round by the spring), a contact switch is closed whereupon the dynamo winds up the spring again exactly as the train and fly wind up the spring in fig. 15. These clocks require a good deal of power, and not being always trustworthy seem to have gone out of use. A contrivance of this kind now in use is that patented by F. Hope Jones and G.B. Bowell, and is represented in fig. 32. A pendulum is driven by the scape-wheel A, and pallets B B in the usual way. The scape-wheel is driven by another wheel C which, in turn, is driven by the weighted lever D supported by click E engaging the ratchet wheel F. This lever is centred at G and has an extension H at right angles to it. J is an armature of soft iron pivoted at K and worked by the electromagnet M. D gradually falls in the act of driving the clock by turning the wheels C and A until the contact plate on the arm H meets with the contact screw L at the end of the armature J, thus completing the electrical circuit from terminal T to terminal T′ through the electromagnet M, and through any number of step-by-step dial movements which may be included in the same series circuit. The armature is then drawn towards the magnet with rapid acceleration, carrying the lever D with it. The armature is suddenly arrested by the poles of the magnet, but the momentum of the lever D carries it farther, and the click E engages another tooth of the ratchet F. A quick break of the circuit is thus secured, and the contact at L is a good one, first because the whole of the energy required to keep the clock going, or in other words the energy required to raise the lever D is mechanically transmitted through its surfaces at each operation, and secondly, owing to the arrangement of the fulcrums at G and K which secure a rubbing contact. The duration of the contact is just that necessary to accomplish the work which has to be done, and it is remarkable that when used to operate large circuits of electrically propelled dials the duration accommodates itself to their exact requirements and the varying conditions of battery and self-induction. The ratchet wheel F is usually mounted loosely upon its arbor and is connected to the wheel C by means of a spiral spring, which in conjunction with the back-stop click P maintains the turning force on the wheelwork at the instant when the lever D is being raised.
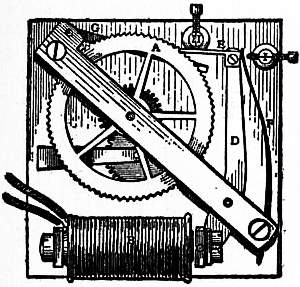 |
| Fig. 33.—Hope Jones’s Dial-driving Device. |
Electrically driven dials usually consist of a ratchet wheel driven by an electrically moved pall. Care has to be taken that the pushes of the pall do not cause the ratchet wheel to be impelled too far. The anchor escapement of a common grandfather’s clock can be made to drive the works by means of an electromagnet, the pendulum being removed. With a common anchor escapement the scape-wheel can be driven round by wagging the anchor to and fro. All then that is necessary is to fix a piece of iron on the anchor so that its weight pulls the anchor over one way, while an electromagnet pulls the iron the other. Impulses sent through the electromagnet will then drive the clock. If the clock is wound up in the ordinary way the motion will be so much helped that the electric current has very little to do, and thus may be very feeble. Fig. 33 shows the dial-driving device of Hope Jones’s clock. Each time that a current is sent by the master-clock, the electromagnet B attracts the pivoted armature C, and when the current ceases the lever D with the projecting arm E is driven back to its old position by the spring F, thus driving the wheel A forward one division. G is a back-stop click, and H, I, fixed stops.
It seems doubtful whether in large towns a number of dials could be electrically driven from a distance because of the large amount of power that would have to be transmitted. But for large buildings, such as hotels, they are excellent. One master-clock in the cellar will drive a hundred or so placed over the building. The master-clock may itself be driven by electricity, but it will require the services from time to time of some one to correct the time. Even this labour may be avoided if the master-clock is synchronized, and as synchronization requires but a small expenditure of force, it can be done over large areas. Hence the future of the clock seems to be a series of master-clocks, electrically driven, and synchronized one with another, in various parts of a city, from each of which a number of dials in the vicinity are driven. Electrical synchronization was worked out by Louis Bréguet and others, and a successful system was perfected in England by J.A. Lund. The leading principle of the best systems is at each hour to cause a pair of fingers or some equivalent device to close upon the minute hand and put it exactly to the hour. Other systems are designed to retard or to accelerate the pendulum, but the former appears the more practical method. There is probably a future before synchronization which will enable the services of a clockmaker to be largely dispensed with and relegate his work merely to keeping the instruments in repair.
Miscellaneous Clocks.—Some small clocks are made to go for a year. They have a heavy balance wheel of brass weighing about 2 1b and about 2½ in. in diameter, suspended from a point above its centre by a fine watch spring about 4 in. long. The crutch engages with the upper part of the spring, and as the balance wheel swings the pallets are actuated. The whole clock is but a large watch with a suspended balance wheel, oscillating once in about 8 seconds. Unless the suspension spring be compensated for temperature, such clocks gain very much in winter.
An ingenious method of driving a clock by water has been proposed. As the pendulum oscillates to one side, an arm on it rises and at last lightly touches a drop of water hanging from a very fine nozzle; this drop is taken off and carried away by the arm, to be subsequently removed by adhesion to an escape funnel placed below the arm. Hence at each double vibration of the pendulum part of the work done by a drop of water falling through a short distance is communicated to the pendulum, which is thus kept in motion as long as the water lasts. At this rate a gallon of water ought to drive the clock for 40 hours. Care of course must be taken to keep the water in the reservoir at a constant level, so that the drops formed shall be uniform.
If it were worth while, no doubt the oscillations of a pendulum working in a vacuum could be maintained by the communication and discharge at each oscillation of a slight charge of electricity; or again, heat might at each oscillation be communicated to a thermo-electric junction, and the resulting current used to drive the pendulum.
The expansions and contractions of metal rods under the influence of the changes of temperature which take place in the course of each night and day have also been employed to keep a clock wound up, and if there were any need for it no doubt a small windmill rotating at the top of a tower would easily keep a turret clock fully wound, by a simple arrangement which would gear the going barrel of the clock to the wind vane motion, whenever the weight had fallen too low, and release it when the winding up was completed. Even a smoke jack would do the same office for a kitchen clock.
The methods of driving astronomical telescopes by means of clockwork will be found in the article Telescope. Measurements of small intervals of time are performed by means of chronographs which in principle depend on the use of isochronous vibrating tuning-forks in place of pendulums. In practice it is needful in most cases that an observer should intervene in time measurements, although perhaps by means of a revolving photographic film a transit of the sun might be timed with extraordinary accuracy. But if the transit of a star across a wire is to be observed, there is no mode at present in use of doing so except by the use of the human eye, brain and hand. Hence in all such observations there is an element of personal error. Unfortunately we cannot apply a microscope to time as we can to space and make the cycle of events that takes place in a second last say for five minutes so as to time them truly. By personal observations the divisions of a second cannot in general be made more accurately than to 1⁄10 or 1⁄15 of a second. The most rapid music player does not strike a note more than 10 or 12 times in a second. It is only in case of recurring phenomena that we can make personal observations more accurate than this by taking the mean of a large number of observations, and allowing for personal error. For the purpose of determining longitude at sea accuracy to 1⁄30 of a second of time would find the place to about 20 yards. It seems to follow that the extent to which astronomical clocks can be made accurate, viz. to 1⁄30 of a second average variation from their mean daily rate, or one two-and-a-half millionth of 24 hours, is a degree of accuracy sufficient for present purposes, and it seems rather doubtful whether mechanical science will in the case of clocks be likely to reach a much higher figure.
In the 17th century it was a favourite device to make a clock show sidereal time as well as mean solar time. The length of the sidereal day is to the mean solar day as .99727 to 1, and various attempts have been made by trains of wheels to obtain this relation—but all are somewhat complicated.
Magical clocks are of several kinds. One that was in vogue about 1880 had a bronze figure on the top with outstretched arm holding in its hand the upper part of the spring of a pendulum, about 10 in. long. The pendulum had apparently no escapement and the puzzle was how it was maintained in motion. It was impossible to detect the mystery by the aid of the eye alone; the truth, however, was that the whole figure swung to and fro at each oscillation of the pendulum, to an amount of 1⁄400 of an inch on the outside rim of the base. A movement of 1⁄400 of an inch per half second of time is imperceptible; it would be equivalent to perception of motion of the minute hand of a clock about 6 in. in diameter, which is almost impossible. The connexion of the figure to the anchor of the escapement was very complicated, but clocks of the kind kept fair time. A straw, poised near the end on a needle and with the short end united by a thread to the bronze figure, makes the motion apparent at once and discloses the trick. Another magical clock consists of two disks of thin sheet glass mounted one close behind the other, one carrying the minute hand and the other the hour hand. The disks rest on rollers which rotate and turn them round. The front and back of the movable disks are covered by other disks of glass surrounded by a frame, so that the whole looks simply like a single sheet of glass mounted in a frame, in the centre of which the hands rotate, without any visible connexion with the works of the clock.
Clocks have been made with a sort of balance wheel consisting of a thread with a ball at the end which winds backwards and forwards spirally round a rod. In others a swing or see-saw is attached to the pendulum, or a ship under canvas is made to oscillate in a heavy sea. In others the time is measured by the fall of a ball down an inclined plane, the time of fall being given by the formula t = √(2s/g sin a), where s is the length of the incline and a the inclination. But friction so modifies the result as to render experiment the only mode of adjusting such a clock. Sometimes a clock is made to serve as its own weight, as for instance when a clock shaped like a monkey is allowed to slide down a rope wound round the going barrel. Or the clock is made of a cylindrical shape outside and provided with a weighted arm instead of a going barrel; on being put upon an incline, it rolls down, and the fall supplies the motive power.
Clocks are frequently provided with chimes moved exactly like musical boxes, except that the pins in the barrel, instead of flipping musical combs, raise hammers which fall upon bells. The driving barrel is let off at suitable intervals. The cuckoo clock is a pretty piece of mechanism. By the push of a wire given to the body of the bird, it is bent forward, the wings and tail are raised and the beak opened. At the same time two weighted bellows measuring about 1 × 2 in. are raised and successively let drop. These are attached to small wooden organ pipes, one tuned a fifth above the other, which produce the notes. Phonographs are also attached to clocks, by which the hours are called instead of rung.
Clocks are also constructed with conical pendulums. It is a property of the conical pendulum that if swung round, the time of one complete revolution is the same as that of the double vibration of a pendulum equal in length to the vertical distance of the bob of the conical pendulum below its point of support. It follows that if the driving force of such a pendulum can be kept constant (as it easily can by an electric contact which is made at every revolution during which it falls below a certain point) the clock will keep time; or friction can be introduced so as to reduce the speed whenever the pendulum flies round too fast and hence the bob rises. Or again by suitable arrangements the bob may be made to move in certain curves so as to be isochronous. Plans of this kind are employed rather to drive telescopes, phonographs and other machines requiring uniform and steady movement.
Comical and performing clocks were very popular in the 15th and 16th centuries. One at Basel in Switzerland was arranged so as gradually to protrude a long tongue as the pendulum vibrated. It is still to be seen there in the museum. The famous clock at Strassburg, originally constructed in 1574, remade in 1842, displays a whole series of scenes, including processions of the apostles and other persons, and a cock that crows. A fine clock at Venice has two rather stiff bronze giants that strike the hours.
Clocks with complicated movements representing the positions of the heavenly bodies and the days of the week and month, allowance being made for leap year, were once the delight of the curious. Repeating clocks, which sounded the hours when a string was pulled, were once popular. The string simply raised the lifting piece and let the clock strike as the hands would do when they came to the hour. This was of use in the old days when the only mode of striking a light at night was with a flint and steel, but lucifer matches and the electric light have rendered these clocks obsolete.
 |
| Fig. 34.—Curve of Variation of daily rate. |
Testing Clocks.—The average amount by which a clock gains or loses is called its mean or average daily rate. A large daily rate of error is no proof that a clock is a bad one, for it might be completely removed by pendulum adjustment. What is required is that the daily rate shall be uniform, that is, that the clock shall not be gaining (or losing) more on one day than on another, or at one period of the same day than at another. In fig. 34 A B is a curve in which the abscissae represent intervals of time, the ordinates the number of seconds at any time by which the clock is wrong. The curve C D is one in which the ordinates are proportional to the tangents of the angles of inclination of the curve A B to the axis of x, that is dy/dx. Whenever the line A B is horizontal, C D cuts the axis of x. In a clock having no variation in its daily rate the curve A B would become a straight line, though it might be inclined to the axis of x, and C D, also a straight line, would be parallel to the axis of x, though it might not coincide with it. In a clock set to exact time and having no variations of daily rate, both the curves would be straight lines and would coincide with the axis of x. The curve C D, known as the curve of variation of daily rate, will generally be found to follow changes of day and night, and of temperature, and the fluctuations of the barometer and hygrometer; it is the curve which reveals the true character of the clock. Hence in testing a clock two things have to be determined: first, the daily rate of error, and second, the average variations from that daily rate, in other words the irregularities of going. To test a clock well six months’ or a year’s trial is needed, and it is desirable to have it subjected to considerable changes of temperature.
Decorative Aspects.—In art the clock occupies a position of considerable distinction, and antique examples are prized and collected as much for the decorative qualities of their cases as for the excellence of their time-keeping. French and English cabinet-makers have especially excelled, although in entirely different ways, in the making of clock cases. The one aimed at comely utility, often made actually beautiful by fit proportion and the employment of finely grained woods; the other sought a bold and dazzling splendour in which ornament overlay material. It was not in either country until the latter part of the 17th century that the cabinet-maker’s opportunity came. The bracket or chamber clock gave comparatively little scope to the worker in wood—in its earlier period, indeed, it was almost invariably encased in brass or other metal; and it was not until the introduction of the long pendulum swinging in a small space that it became customary to encase clocks in decorative woodwork. The long or “grandfather” clock dates from about the fourth quarter of the 17th century—what is, perhaps, the earliest surviving English dated specimen is inscribed with the date 1681. Originally it was a development of the dome-shaped bracket clock, and in the older examples the characteristic dome or canopy is preserved. The first time-keepers of this type had oaken cases—indeed oak was never entirely abandoned; but when walnut began to come into favour a few years later that beautifully marked wood was almost invariably used for the choicest and most costly specimens. Thus in 1698 the dean and chapter of St Paul’s cathedral paid the then very substantial price of £14 for an inlaid walnut long-cased eight-day clock to stand in one of the vestries. The rapidity with which the new style came into use is suggested by the fact that while very few long clocks can be certainly dated before 1690, between that year and the end of the century there are many examples. Throughout the 18th century they were made in myriads all over England, and since they were a prized possession it is not surprising that innumerable examples have survived. Vary as they may in height and girth, in wood and dial, they are all essentially alike. In their earlier years their faces were usually of brass engraved with cherubs’ heads or conventional designs, but eventually the less rich white face grew common. There are two varieties—the eight-day and the thirty-hour. The latter is but little esteemed, notwithstanding that it is often as decorative as the more expensive clock. The favourite walnut case of the late 17th and early 18th century gave place in the course of a generation to mahogany, which retained its primacy until the introduction of cheaper clocks brought about the supersession of the long-cased variety. Many of these cases were made in lacquer when that material was in vogue; satinwood and other costly foreign timbers were also used for bandings and inlay. The most elegant of the “grandfather” cases are, however, the narrow-waisted forms of the William and Mary period in walnut inlay, the head framed in twisted pilasters. Long clocks of the old type are still made in small numbers and at high prices; they usually contain chimes. During the later period of their popularity the heads of long clocks were often filled in with painted disks representing the moon, by which its course could be followed. Such conceits as ships moving on waves or time with wings were also in favour. The northern parts of France likewise produced tall clocks, usually in oaken cases; those with Louis Quinze shaped panels are often very decorative. French love of applied ornament was, however, generally inimical to the rather uncompromising squareness of the English case, and the great Louis Quinze and Louis Seize cabinetmakers made some magnificent and monumental clocks, many of which were “long” only as regards the case, the pendulum being comparatively short, while sometimes the case acted merely as a pedestal for a bracket-clock fixed on the top. These pieces were usually mounted very elaborately in gilt bronze, cast and chased, and French bracket and chamber clocks were usually of gilded metal or marble, or a combination of the two; this essentially late 18th-century type still persists. English bracket clocks contemporary with them were most frequently of simple square or arched form in mahogany. The “grandfather” case was also made in the Low Countries, of generous height, very swelling and bulbous.
↧ Download as ZWI file | Last modified: 11/17/2022 15:24:24 | 66 views
☰ Source: https://oldpedia.org/article/britannica11/Clock | License: Public domain in the USA. Project Gutenberg License
 ZWI signed:
ZWI signed: KSF
KSF